[算法讲解] KMP & EXKMP : next与extend的羁绊
KMP
KMP作为一个广为人知的字符串匹配算法——也是本文的前一半。
旨在着重讲解next数组的求法,并使读者理解。
#include<iostream> #include<cstring> using namespace std; const int N=5000002; int next[N]; string s1,s2; void init(string s){ for(int i=0,j=next[0]=-1,len=s.size();i<len;){ if(j==-1||s[i]==s[j]) next[++i]=++j; else j=next[j]; } } int main(){ cin >> s1 >> s2; init(s2); for(int i=0,j=0,len=s1.size();i<len;){ if(j==-1||s1[i]==s2[j]) ++i,++j; else j=next[j]; if(j==s2.size())cout << i-s2.size()+1 << endl; }for(int i=1,len=s2.size();i<=len;++i) cout << next[i] << " "; return 0; }
先说两个概念:
真前缀和真后缀
真前/后缀 : 即不包括原字符串的前/后缀。

大致说一下
kmp的过程
1)有两个指针i ,j分别指向文本串T和模式串P , 如下图,长的是T,短的是P。
初值i = j = 0;

2)比较 i=0,j=0,发现不等,此时把i后移一位,相当于把模式串右移一位,比较i=1 j=0。

3) ....一路比较,直到i=3,j=0时才发现相等。 ++i,++j。

4) i=5 , j=1时发现仍然相等.....

5)直到i=10,j=6时,发现不相等。

6)根据暴力的思想,我们应当把i j回到之前,接着“逐位匹配”。像这样。

7)但是本文不讲暴力!让我们回到这张图。
我们其实已经知道了文本串中的后面一个 "AB" 与模式串中的前两位“AB”是相同的,所以为什么不直接把模式串多几格呢?
但是我们怎么知道有两位"AB"相同?其实是因为在不匹配的"D"前面的"AB"匹配了,而这个"AB"与模式串首个“AB”相
同,于是我们就可以这样跳跃。
这个“如何跳跃”,就是next数组。后面详细讲解。

8)如图,把模式串移动到这个位置,i=10,j=2,这样直接使得前面的AB匹配上了,于是比较i=10和j=2,发现不匹配。
那么此时跳到哪里呢?发现在C之前的"AB"中,没有相同的真前后缀,于是只好从头开始了,j=0。

9)比较,匹配不上,++i,j=next[j]=0;

10)过程大致清楚了吧。

11)最后发现了全部匹配 : j=p.size()且p[j]==t[i]。此时重新匹配:j = nest[j] = 0; 即从头。

12) 继续匹配,最后结束。
重头戏:next数组的理解
我们先看到 init 初始化函数。
void init(string s){ for(int i=0,j=next[0]=-1,len=s.size();i<len;){ if(j==-1||s[i]==s[j]) next[++i]=++j; else j=next[j]; } }
当然写成while的也行。
void init(string s) //这里j变成了k .... { int i=0,k=next[0]=-1,len=s.size(); while(i<len) if(k==-1 || s[i]==s[k]) next[++i]=++k; else k=next[k]; }
首先,next[i]= 字符串中0~i-1 部分的最长的真前缀等于真后缀的长度 + 1。
我们一点点来解释"next[i]= 字符串中0~i-1 部分的最长的真前缀等于真后缀的长度 + 1。"
1> "0~i-1"是因为当i不匹配时,只看前面的区间的前后缀,而且若不匹配i并不会++(所以下次还是从当前位比较)。
如果是0~i,那么移动后当前位的字符还是相同的,没有意义。
(正确的)比如P : ABCABC
T : ABCABD
如果最后一个C不匹配了,说明AB匹配,应当把AB后的第一个C(指p[2])拿去匹配。
即:
ABCABD
ABCABC
->
ABCABD
ABCABC
2> "最长的真前缀等于真后缀的长度 + 1"
显然要最长
+1?因为其实下一步需要比较的还是相同前后缀的下一位(别忘了相同部分已经比较过了,要让他们对齐)。
理解了思路之后就要理解代码。
void init(string s){ for(int i=0,j=next[0]=-1,len=s.size();i<len;){ if(j==-1||s[i]==s[j]) next[++i]=++j; else j=next[j]; } }
i,j表示当前处理的区间是0~i,判断的前缀和后缀长度为j,即前缀0~j-1,后缀 i-j+1~i
(其实处理过程就是自己匹配自己)
如果0~i前后缀匹配,则把next[i+1]=j+1,且i++,j++。否则就像匹配文本串时一样,跳到上一个匹配的地方。
if(j==-1)用来特判越界。
也许你会想,-1是什么,为什么不用0呢?
我们先看看-1有什么用。
next[0]=-1,使得更新的是next[++i]=++j=0。也就是没有相同前后缀,必须从头开始匹配。
那么如果next[0]=0呢?显然不行,会使得跳跃时出现错误结果。
j=0同理。
那么kmp就讲完了(什么辣鸡结尾)。
EXKMP
前言
mmp 这个 辣鸡 玩意儿花了我好久才理解,所以我必须得把它给讲清楚了。
不过很少考。(其实我是因为考了才学的)
概念
EXKMP(扩展KMP)用于解决以下问题:
> 给你两个字符串s,t,长度分别为n,m。
> 请输出s的每一个后缀与t的最长公共前缀。
(谁这么无聊出这种题啊)
例题
同样扔代码。
#include<iostream> #include<cstring> #include<cmath> using namespace std; const int N=5000002; int next[N],extend[N]; void init(string s){ int now=0,ls=next[0]=s.size(),idx=0,far; while(s[now]==s[now+1]&&now+1<ls)++now; next[1]=far=now; idx=1; for(int i=2;i<ls;++i){ if(i+next[i-idx]<far) next[i]=next[i-idx]; else { next[i]=max(0,far-i); while(i+next[i]<ls&&s[i+next[i]]==s[next[i]]) ++next[i]; if(i+next[i]>far)far=i+next[i],idx=i; } } } void exkmp(string t,string p){ init(p); // getnext int now=0,lt=t.size(),idx=0,far; while(p[now]==t[now]&&now<lt)++now; extend[0]=far=now; for(int i=0;i<lt;++i){ if(i+next[i-idx]<far) extend[i]=next[i-idx]; else { extend[i]=max(0,far-i); while(i+extend[i]<lt&&t[i+extend[i]]==p[extend[i]]) ++extend[i]; // attention about 0 for starter if(i+extend[i]>far)far=i+extend[i],idx=i; } } } string s,t; int main(){ cin>>s>>t; exkmp(s,t); for(int i=0,len=t.size();i<len;i++)printf("%d ",next[i]); puts(""); for(int i=0,len=s.size();i<len;i++)printf("%d ",extend[i]); return 0; }
首先有(请时刻牢记这个定义,最好用纸笔记一下)
int next[N],extend[N]; string s,t; //均从0开始编号
//next[i]表示 s[i...n]与s的最长公共前缀的长度。
//extend[i]表示 s[i...n]与t的最长公共前缀的长度。
先说extend , (next : 怎么又是我最后)
extend
特殊情况
1) 上面是s,下面是t (t是移动的那个)。绿色为已经匹配上的部分,红色框是失配的地方。下图为第一次匹配,暴力进行。
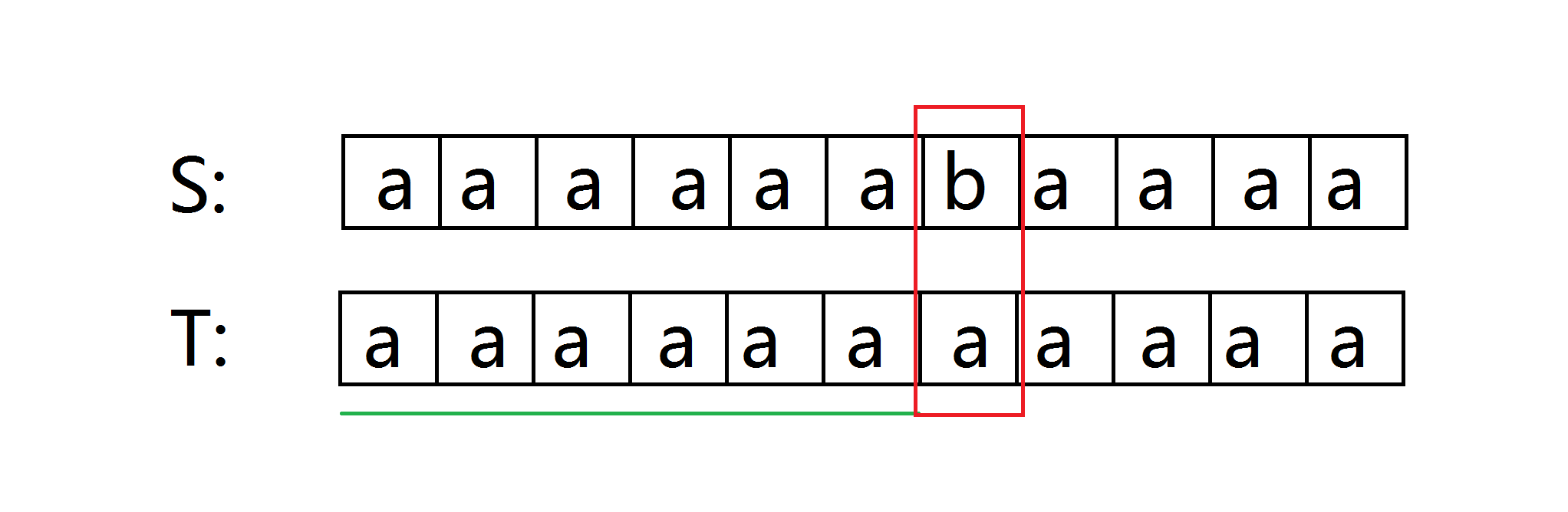
2)看第二步。把t往后移了一位,于是变成了找s[1...n]和t的公共前缀。
红线划掉的地方已经不关我们的事了。
但我们发现此时做了大量的无用功,因为中间有很大的重叠部分。
让我们回到1)处。
由1)得,s[0...5] == t[0...5]
∴ s[1...5] == t[1...5]
此时我们求的是s[1...5]与t的匹配。
于是这个问题就变成了 (s[1...5]=) t[1...5] 与 t的匹配。
还记得那个定义吗? 这就是next数组。
当然一般情况并没有那么简单。

一般情况
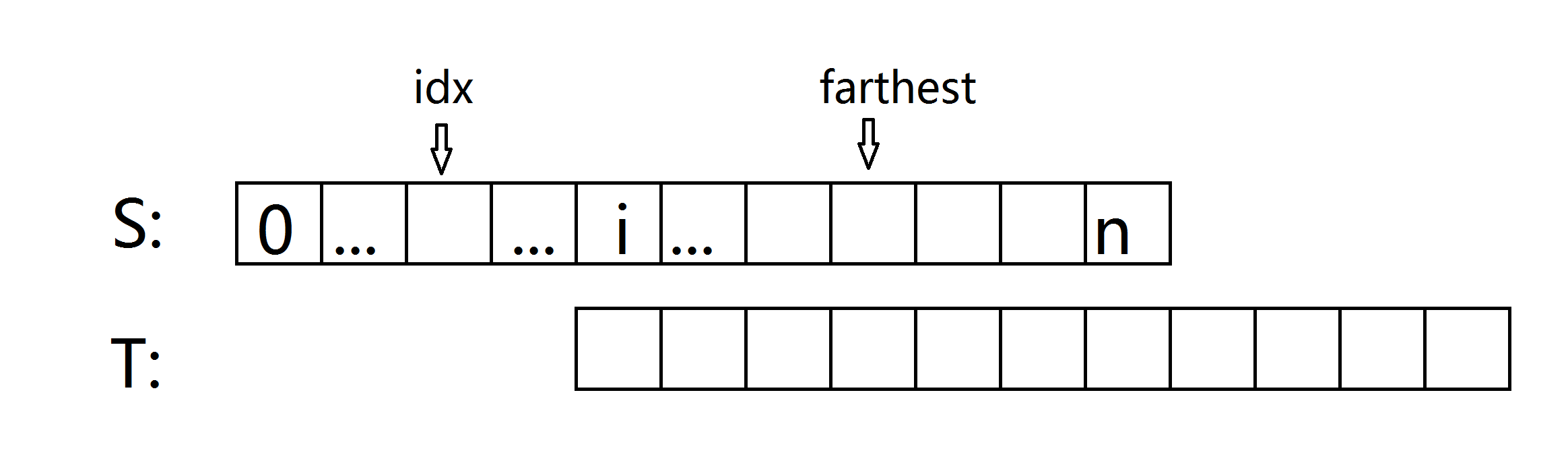
假设当前已经处理好了 extend [0...i) ,也就是正在处理 s[i] 。
记:
1> farthest = max { j + extend[j] | 0 <= j < i} (已经到达的最远位置,即满足0 <= j < i 的 最大的 j+extend[j])
为了方便,farthest 我们用far代替。
2> idx(index) ,使得 j + extend[j]最大的 j。 也就是对应far 的 j。
其实就是这样:
int idx,far=0; for(int j=0;j<i;++j) if(far<j+extend[j]) far=j+extend[j],idx=j;
显然,其实是可以不记录far的,也有这样的写法,但是加加减减的不利于阅读和理解(把far都用idx+extend[idx]代替),所以本文.....就这么讲解。(雾)
现在让我们把t挪一挪,使t[0]对准idx。
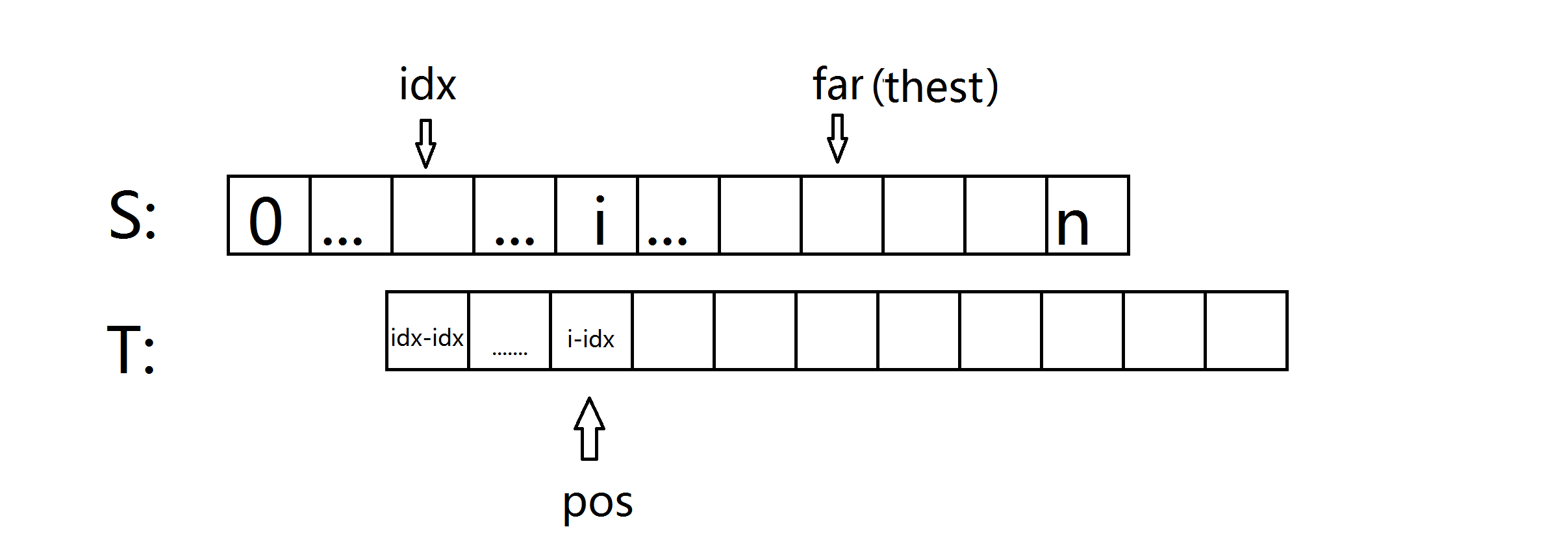
pos,i对应的位置,pos = i-idx。
下面就开始分类咯。
一 、 K+next[pos] < far

如图(这张图稍微调整了一下,希望不影响观看),绿线和蓝线是相等的(雾),也就是说他们表示的区间相等。
他们的长度都等于next[pos]。(看看定义)
再看黄线和蓝线。
我们有 s[idx...far] = t[0 ... far-index](因为index已经匹配过了)
所以s[i ... i+next[pos]] = t[pos ... pos+next[pot]] 也就是黄线和蓝线相等(既然整个都相等那么里面的每一个对应的也相等)
所以绿线 = 蓝线 = 黄线
咱们把t再挪回来。
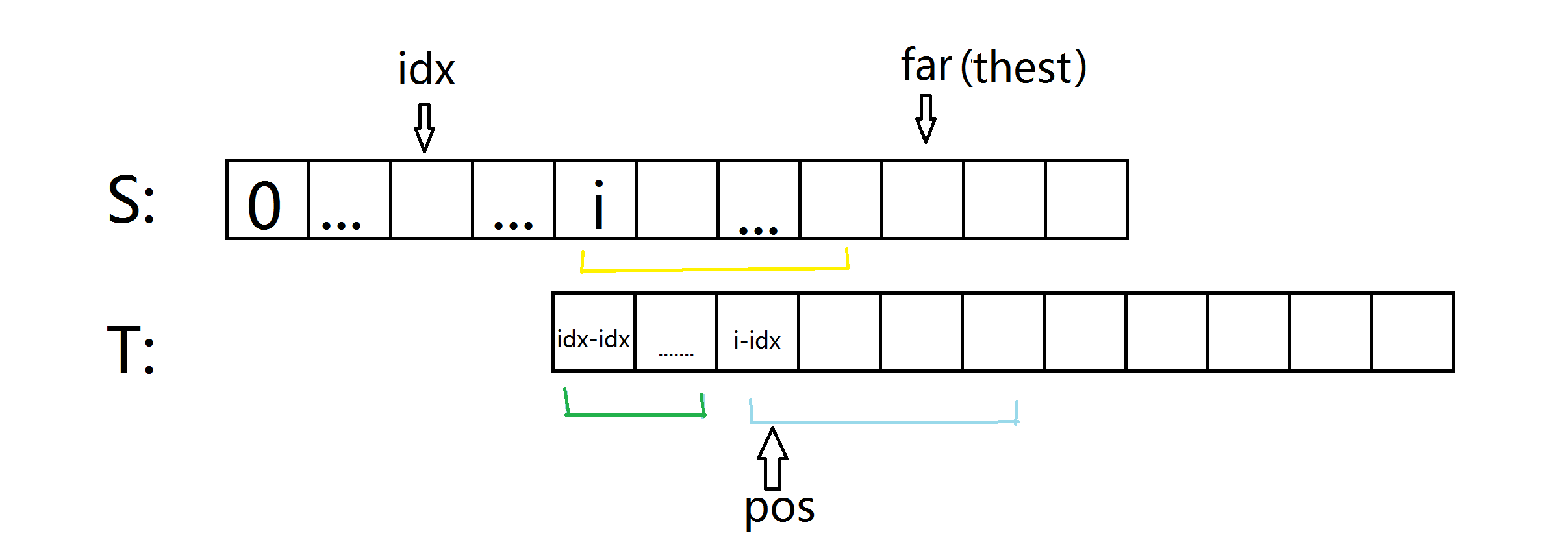
别光看这诡异的图啊.....绿线和黄线是相等的....
但是黄线 = extend[i]
绿线 = next[i-idx]
所以此时有:
if(i+next[i-idx]<far) extend[i]=next[i-idx];
不过这里可能有人要问,(因为含在[idx,far]内)黄线和蓝线的后一位不是也相等吗?为什么不会导致错误呢?
回到问题的实质上来,我们要求的是extend[i],也就是比较黄线和绿线,倘若绿线的下一位也与他们相等,则必然next[pos]就会+1,就不是这个值了,所以仍是正确结果。
不过由此我们也发现,如果黄线末端是far位置,则不知道下一位与蓝线下一位的关系了,这时便不能这样处理,在下一类中。(看看这部分的标题,只有<号)
二、K+next[pos]>=far
这种也很好理解啦,我们只取等同于前面一种的一定相同的部分,后面的再暴力比较不就完事儿了吗?
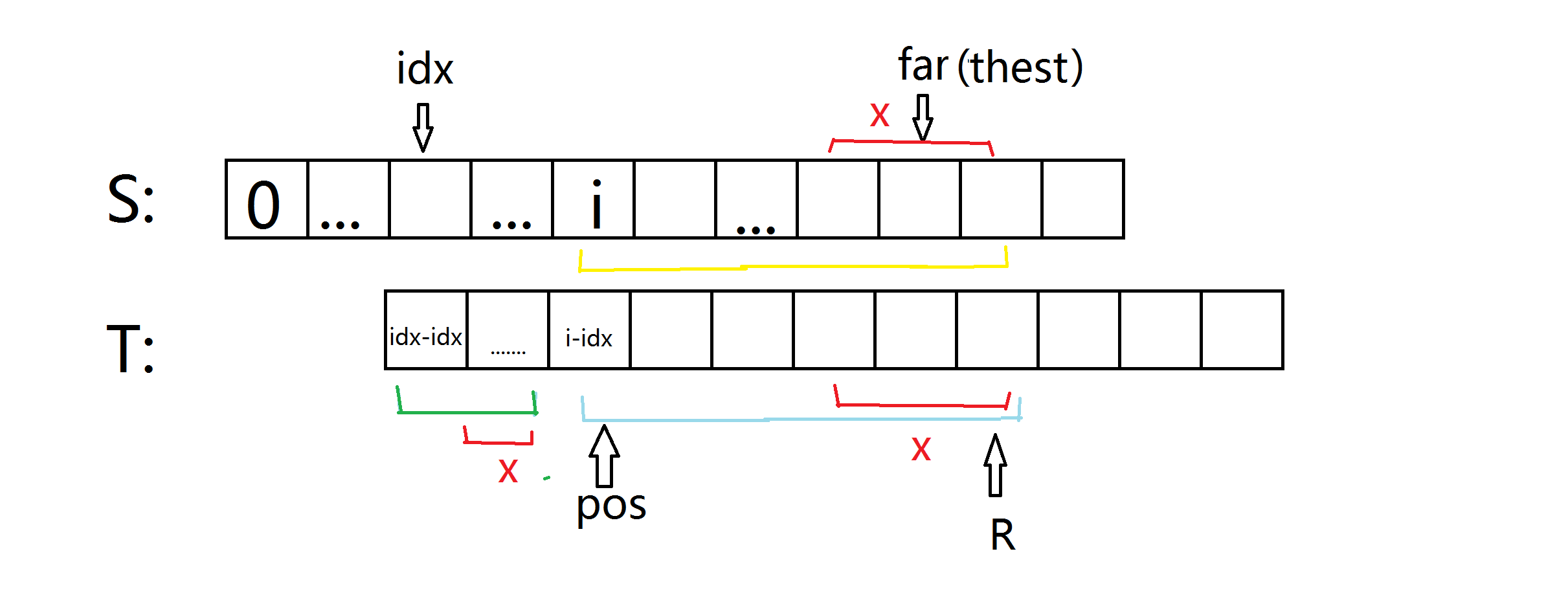
R只是一个讲解的时候稍微简化一下用的,代码用不着,R=pos+next[pos] 。
R在s中对应的是i+next[pos] , 它 >= far。
X代表超过far的长度。X=i+next[pos]-far+1。
他使得 i+next[pos]-X=far-1。
这样在三条线都去掉X部分的情况下即可化归为上一种情况。
但是还要判断后面的字符,于是从far开始,直接暴力比较。
but , 您又发现,far不一定会 > i 呀 。得,没事,那就从头暴力吧。
void exkmp(string t,string p){ init(p); // getnext int now=0,lt=t.size(),idx=0,far; while(p[now]==t[now]&&now<lt)++now; extend[0]=far=now; for(int i=0;i<lt;++i){ if(i+next[i-idx]<far) extend[i]=next[i-idx]; else { extend[i]=max(0,far-i); while(i+extend[i]<lt&&t[i+extend[i]]==p[extend[i]]) ++extend[i]; if(i+extend[i]>far)far=i+extend[i],idx=i; } } }
第一遍因为没有far所以直接暴力。
第一次暴力用剩下的now与后面的now一点关系都没有,相当于是两个变量!并不是要接着上一次的now什么的。
当然,要注意暴力时判出界,最后还要更新idx和far。
那么extend讲完了。
下面讲next。
next
next的意义和extend很像,所以做法几乎是一样的。
不过next[0]显然就等于原串长,next[1]直接暴力,所以从next[2]开始。
void init(string s){ int now=0,ls=next[0]=s.size(),idx=0,far; while(s[now]==s[now+1]&&now+1<ls)++now; next[1]=far=now; idx=1; for(int i=2;i<ls;++i){ if(i+next[i-idx]<far) next[i]=next[i-idx]; else { next[i]=max(0,far-i); while(i+next[i]<ls&&s[i+next[i]]==s[next[i]]) ++next[i]; if(i+next[i]>far)far=i+next[i],idx=i; } } }
ls?注意,本文不讲解任何树!ls是len_of_string !
这里注意虽然next[0]很长,但是idx不能为0,far也不能为原串长!否则next[i]=next[i-idx]等于没用。(哪有白嫖的好事)
其它的就是把extend 都改成next , 字符串名也改一下罢了。
完结撒花!(雾)
Z算法(Z-algorithm)
Z算法就是把next和extend合并成同一个数组z,可以简化一下代码。因为窝太弱了还不会所以就不写了。
END~


 浙公网安备 33010602011771号
浙公网安备 33010602011771号