splay:从试图理解到选择背板
前言
Splay(伸展树)作为平衡树家族中最著名的一员,又可以作为LCT的辅助树 ——
这就是我先学它以及本文讲解它的理由(小声)
它能作为Link Cut Tree的辅助树是因为Splay可以进行独特的区间翻转,其他树 我不知道, 大概是不能。
这个玩意又是Tarjan发明的。 (%%%Tarjan)
这篇题解会涉及一些其它题解没有的玩意儿,来帮助读者更好的理解Splay的实现。
不知道什么是平衡树的自行度娘。
Splay的核心思想
就是通过不断的改变树的形态来保证树不会(一直)是一条链,从而保证复杂度。
基本操作
在以下代码中:
struct TREE{ int f,val,w,siz;
//该节点的父亲, 值, 相同值的个数(有时候为1,可去掉这个域), 子树大小(就是包括自己,下面有几个节点) int ch[2];
//0:左儿子 1:右儿子 (方便利用表达式进行操作)
int tag;
//区间翻转的标记 }t[N],_NULL;
//树 和一个空白 int root,tot;
//根节点的序号 节点个数 queue<int>rec;
//回收节点的队列 #define LS (t[u].ch[0]) #define RS (t[u].ch[1])
首先是单旋rotate ,使得X向上一位。先上代码。
void push_up(int u){ //计算size大小 t[u].siz=t[u].w+t[LS].siz+t[RS].siz; } void Connect(int son,int fa,int rel){ //儿子 父亲 哪个儿子(左/右) t[fa].ch[rel]=son; t[son].f=fa; } void rotate(int X){ int Y=t[X].f,Z=t[Y].f; int B=t[X].ch[t[Y].ch[0]==X], X_pos=t[Y].ch[1]==X; int Y_pos=t[Z].ch[1]==Y; Connect(B,Y,X_pos); Connect(Y,X,X_pos^1); //✔!X_pos Connect(X,Z,Y_pos); push_up(Y); push_up(X); }
上几张图来讲解一下,尤其是那几个奇怪的Connect。
首先单旋的过程是这样的:显然大小关系不变

图1中原来的大小关系是A<X<B<Y<C,再看旋转后,还是如此。
而图2亦是。
那么如何实现呢?
先看相对位置改变了的点,只有X,Y,B,其它的点相对位置不变,可以不用管。
那么我们记录下需要的点和一些关系(其实也可以不记录),再重新连线即可,如下图(顺序不唯一)
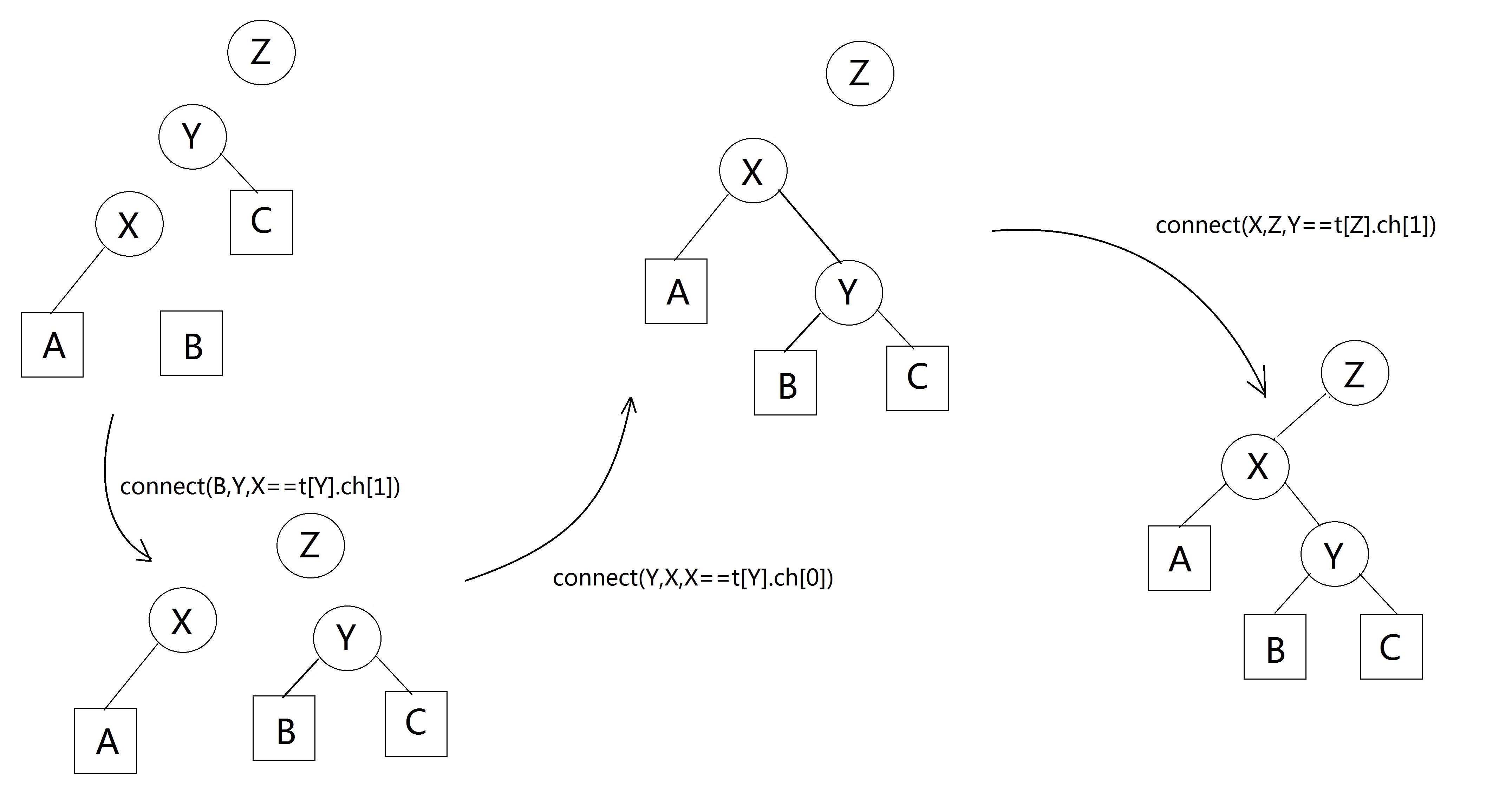
我们再来看看代码:和上图描述的一样。
void rotate(int X){ //let X be his grandparent's son int Y=t[X].f,Z=t[Y].f; int B=t[X].ch[t[Y].ch[0]==X], X_pos=t[Y].ch[1]==X; int Y_pos=t[Z].ch[1]==Y; Connect(B,Y,X_pos); Connect(Y,X,X_pos^1); //✔!X_pos Connect(X,Z,Y_pos); push_up(Y); push_up(X); }
注意这里X_pos指的是(原来)X在Y的位置(能理解吧),B是X下位于X_pos^1或者说!X_pos的儿子。也就是Y-X-B形成了一个折的形状。
如果不记得怎么连的话,画个图,去掉无用的边,然后找到一种连边顺序就行,如果像我这样使用变量记录的话,就可以不用考虑顺序,随便连这三条,否则要注意是否会调用已经被修改的量,但是也不难。
记得push_up。
那么下一个操作,最重要的也是最有特色的:伸展(双旋)splay
void splay(int X,int goal){ //let X be goal's son while(t[X].f!=goal){ int Y=t[X].f,Z=t[Y].f; if(Z!=goal) (t[Z].ch[0]==Y)^(t[Y].ch[0]==X) ?rotate(X):rotate(Y); rotate(X); } if(!goal)root=X; }
goal是什么?山羊的自行百度吧。
我们的目标是让X成为goal的 亲 儿子。
首先在满足t[X].f!=goal的条件下循环(废话如果已经是儿子了还旋转来干嘛)。
所谓双旋就是一次(循环)旋转两次。
上图。
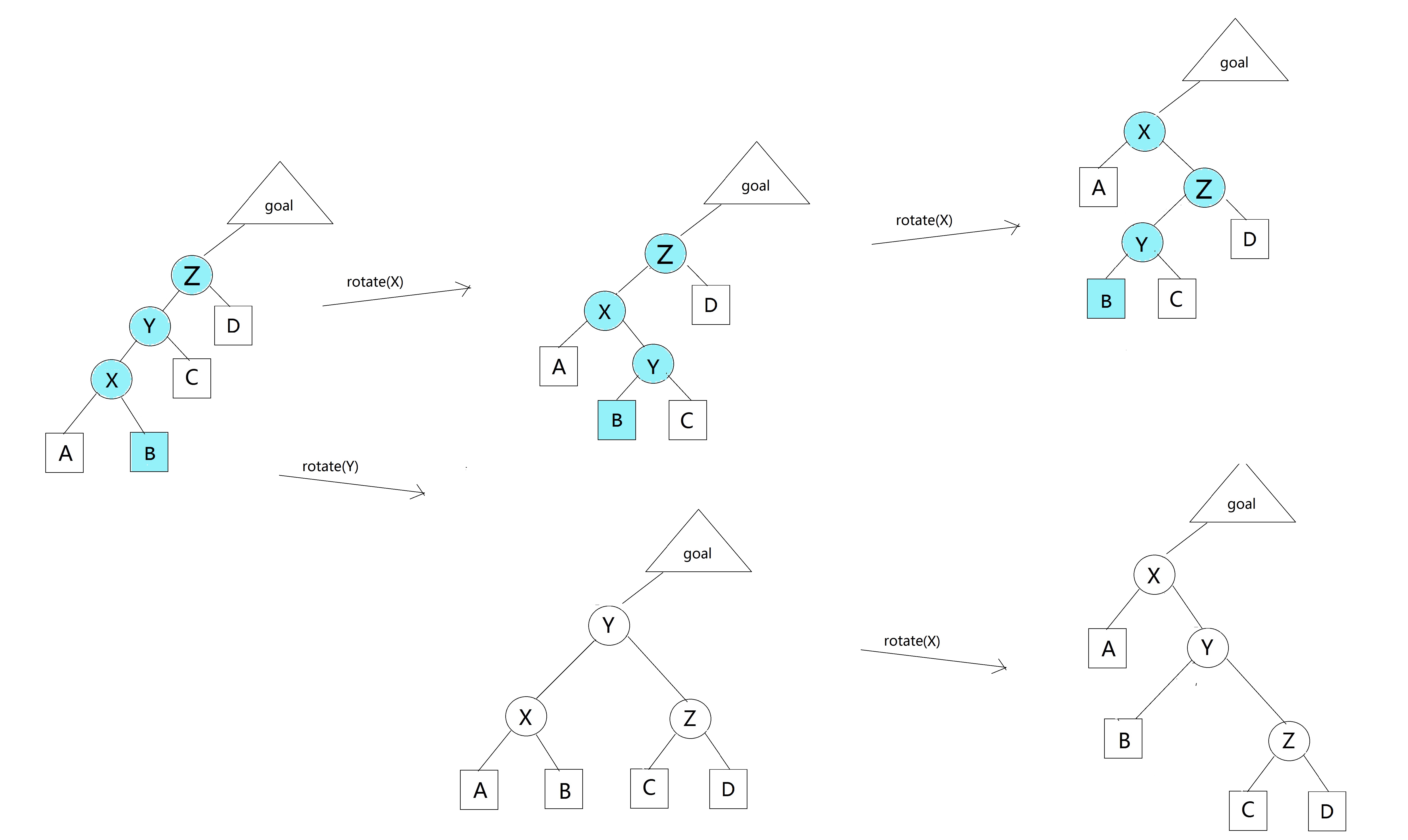
我们发现,第一次可以旋转X也可以旋转Y,但是第二次只能旋转X(不然就到不了goal下面了)。
但是我们又发现(woc怎么又发现了)第一种旋转Y再旋转X,最后有一条链 Z->Y->X->B成为了X->Z->Y->B相当于没有改变,也就是说此时不能让树更优。
这是X对于Y和Y对于Z相同的情况(即(t[Y].ch[1]==X) == (t[Z].ch[1]==Y)),还有不相同的情况,你们自己画吧反正就会 发现这是要先旋转X,也就是连续旋转两次X
woc算了我把它画出来吧,毕竟本来就是为了服务于人民(雾)。不过先Y后X的情况不知道为什么崩了,莫非我画错了么.....烦请大佬指出。
那么代码就出来了,两个位置不相同的就YX,相同就XX。
再放代码,省的你们去翻上面。
当然别忘了判定旋转到根的情况。
(异或:相同则真,不同则假 a^b 等价于 a&&b || !a&&!b 或者 !(a&&!b || !a&&b))
void splay(int X,int goal){ //let X be goal's son while(t[X].f!=goal){ int Y=t[X].f,Z=t[Y].f; if(Z!=goal) (t[Z].ch[0]==Y)^(t[Y].ch[0]==X) ?rotate(X):rotate(Y); rotate(X); } if(!goal)root=X; }
让我们看到下一个操作查找find
find的原理是对每个节点通过val值与X比较判断X的位置,选择向哪个儿子寻找,如果存在X,最后一定能找到,如果不存在,则找到X的前驱/后继,最后把这个数旋转到根节点。
如果不了解什么是前驱/后继,请先看下一个操作。
这里用反证法解释一下为什么会是前驱/后继,就拿前驱来说:
我们假设被查数X,而find找到的数是A,并且树中存在一个数B,满足A<B<X,中间没有其它数。
那么B一定是A的右儿子,此时程序并不会停在A的位置而是继续向下,到B,显然矛盾。
所以找到的一定是 X 或 前驱 或后继。
void find(int X){ int u=root; while(t[u].ch[X>t[u].val]&&t[u].val!=X) u=t[u].ch[X>t[u].val]; splay(u,0); }
接下来是前驱lower/后继upper
对于一个数X,有:
前驱:比X大的最小数;
后继:比X小的最大数。
首先用find找到X的位置,特判正好是前驱/后继的情况,然后以前驱来说,从root的左儿子开始,一直找右儿子,最后就是前驱。
根节点就是X,左儿子的数都比X小,再一直向右,越来越大,但是一定比X小,那显然就是前驱了。后继同理。
你可能会说,要是根节点是X的后继而我们要找的是前驱怎么办?
举个栗子:在1 3 5 7中寻找X=6的前驱,显然答案是5。
出于某种原因我们找到的根节点是7,于是按照找到X的步骤进行处理,找7的前驱,
没毛病,还是5。
原因在于这颗树里面并没有X这个数,也就是说此时X的前驱和后继是相连续的,那么就不会影响。
int lower(int X){ //find the first number that //is lower than X find(X); if(t[root].val<X)return root; int u=t[root].ch[0]; while(RS) u=RS; splay(u,0); return u; } int upper(int X){ find(X); if(t[root].val>X)return root; int u=t[root].ch[1]; while(LS) u=LS; splay(u,0); return u; }
下一个:插入_insert 和 删除_delete
首先是插入操作,模仿find,找到合适的位置放入新数即可。
注意要记录father,而且路径上的数size++。
区分数字是否存在重复(相同数是否共用节点)。
找到相同的数字直接累加次数即可。
否则同不重复,直接新建节点,赋各种信息。
如果需要可以写节点回收队列,记录已经删除的节点,下次直接用这个编号。
(有些题目可以一次性建树,不用一个一个来)
//数字有重复
void _insert(int X){ int u=root,f=0; while(u&&t[u].val!=X){ ++t[u].siz; f=u; u=t[u].ch[X>t[u].val]; } if(!u){ if(rec.empty())u=++tot; else u=rec.front(),rec.pop(); t[u].f=f; t[u].val=X; t[u].w=t[u].siz=1; LS=RS=0; if(f)t[f].ch[X>t[f].val]=u; }else{ ++t[u].w; ++t[u].siz; } splay(u,0); }
//数字无重复
void insert(int x){ int u=root,f=0; while(u)f=u,u=t[u].ch[x>t[u].val]; u=++tot; t[f].ch[x>t[f].val]=u; t[u].f=f; t[u].siz=1; t[u].val=x; if(!root)root=u; splay(u,0); }
删除操作。
如果像find和insert那样的话呢?
我们考虑到X节点上有老下有小,他走了以后两个儿子无人接管,又不能交给他的父亲(会导致节点数目和节点关系不对),于是我们不得不——让他没有儿子。
先看代码吧。
void _delete(int X){ int pre=lower(X),last=upper(X); splay(pre,0);splay(last,pre); int u=t[last].ch[0]; if(t[u].w>1){ --t[u].w; --t[u].siz; splay(u,0); }else{ rec.push(u); t[last].ch[0]=0; t[u]=_NULL; } push_up(last); push_up(pre); }
这个做法非常的巧妙,先找到X的前驱和后继,在把前驱转到根,把后继转到前驱下面,这样前驱的左儿子 <前驱 <X ,而后继的右儿子 >后继 >X,所以后继的左儿子就只剩X了,而且X没有儿子,可以直接删除(一样分两种情况),最后别忘了push_up。
但是我们发现最小数和最大数找不到前驱/后继.....这时候我们选择插入-INF INF两个节点,作为他们的前驱/后继,这个后面慢慢讲。
排名查询Rank
int Rank(int X){ find(X);int u=root; return t[u].val==X?t[LS].siz+1:-1; }
好短。
找到X输出比他小的数的个数+1,应该不难理解。
至于-1只是拿来判定是否存在X的,其实很多题目都会保证X存在。
第K大 Kth(从小到大的第K个数)
int Kth(int K){ int u=root; if(t[u].siz<K)return INF; while(K<=t[LS].siz||K>t[LS].siz+t[u].w){ //Attention if(K>t[LS].siz+t[u].w)//✔K-=t[LS].siz+t[u].w; K=K-t[LS].siz-t[u].w,u=RS; else u=LS; } splay(u,0); return t[u].val; }
有点像Rank?
反正都是利用当前数在当前区间的排名就是左儿子大小+1。
对于每个节点,如果K小于当前节点的排名,就往左儿子找,大于就往右儿子找,并减去当前数的排名。
注意如果数字重复的话,只要数字的排名区间包含K就行。
为什么向右要减去排名呢?
因为右儿子下面的儿子的siz显然并不包括左儿子的那些数。
这也是为什么前面说当前区间。
下一个操作!区间翻转split(貌似很多时候这个操作和上面的不会一起考?)
void split(int l,int r){ int L=Kth(l),R=Kth(r+2); splay(L,0);splay(R,L); int u=t[root].ch[1]; u=LS; t[u].tag^=1; }
是不是和删除操作很像?
其实就是找到 l-1 和 r+1然后把整个区间一夹,打个翻转标记(如果原来已经有标记则消除)就好啦。
为什么是Kth?我们怎么能够去找l和r+2这两个数字(强调!)的前驱后继呢!我们要找的是整个区间的第l 、 r+2个数,所以是Kth。
不是l-1和r+1?之前不是说还有个INF和-INF吗,因为这里用的是Kth而不是前驱后继所以要算上-INF的一个位置,分别+1。
为什么说一般不会一起考呢?(插入删除当然可能...)因为这个操作是拿来维护区间的啊...况且这里的Kth其实可以理解为区间放在数组里的下标,也就是位置,和元素的大小没有关系。
有了split怎么能没有下推标记push_down呢!
void push_down(int u){ if(!t[u].tag)return; t[u].tag=0; t[LS].tag^=1; t[RS].tag^=1; swap(LS,RS); //swap in two numbers (ch[0] & ch[1]) }
很好理解,标记下传一下,左右子树交换即可(交换ch[0] ch[1]的值就好啦)。
这里要注意有了标记之后Kth要改变!
因为左右子树被交换了,值会不同,长度也不同,所以一路上push_down。
其它函数不变。甚至splay也不变,因为splay每次都在函数最后操作,一定都被push_down过了。
int Kth(int k){ int u=root; while(true){ push_down(u); //Must if(k<=t[LS].siz) u=LS; else if(k>t[LS].siz+1) k-=t[LS].siz+1,u=RS; else return u; } splay(u,0); return u; }
注意事项
所有函数后面调用一次splay把当前处理的节点转到根。
哨兵节点
在所有操作前,要插入两个哨兵节点,-INF和INF,他们的w(重复次数)和siz(子树大小)在插入后直接置0(在后面由于有了儿子,它的siz可能不是0,但push_up是不会把他算进去)。
这两个节点的作用是保证每个数都有前驱和后继,并且保证split能够找到节点。
root不用重置,且初值为0即可。
_insert(INF);_insert(-INF); t[1].siz=t[2].siz=t[1].w=t[2].w=0;
例题两道
附一下代码。
//luoguP3369 #include<iostream> #include<algorithm> #include<cstdio> #include<cmath> #include<queue> #include<cctype> using namespace std; const int N=1e6,INF=0x7fffffff; namespace SPLAY{ struct TREE{ int f,val,w,siz; int ch[2]; }t[N],_NULL; int root,tot; queue<int>rec; #define LS (t[u].ch[0]) #define RS (t[u].ch[1]) void push_up(int u){ //get t[u].siz t[u].siz=t[u].w+t[LS].siz+t[RS].siz; } void Connect(int son,int fa,int rel){ //son father & relation t[fa].ch[rel]=son; t[son].f=fa; } void rotate(int X){ //let X be his grandparent's son int Y=t[X].f,Z=t[Y].f; int B=t[X].ch[t[Y].ch[0]==X], X_pos=t[Y].ch[1]==X; int Y_pos=t[Z].ch[1]==Y; Connect(B,Y,X_pos); Connect(Y,X,X_pos^1); //✔!X_pos Connect(X,Z,Y_pos); push_up(Y); push_up(X); } void splay(int X,int goal){ //let X be goal's son while(t[X].f!=goal){ int Y=t[X].f,Z=t[Y].f; if(Z!=goal) (t[Z].ch[0]==Y)^(t[Y].ch[0]==X) ?rotate(X):rotate(Y); rotate(X); } if(!goal)root=X; } void find(int X){ int u=root; while(t[u].ch[X>t[u].val]&&t[u].val!=X) u=t[u].ch[X>t[u].val]; splay(u,0); } int lower(int X){ //find the first number that //is lower than X find(X); if(t[root].val<X)return root; int u=t[root].ch[0]; while(RS) u=RS; splay(u,0); return u; } int upper(int X){ find(X); if(t[root].val>X)return root; int u=t[root].ch[1]; while(LS) u=LS; splay(u,0); return u; } void _insert(int X){ int u=root,f=0; while(u&&t[u].val!=X){ ++t[u].siz; f=u; u=t[u].ch[X>t[u].val]; } if(!u){ if(rec.empty())u=++tot; else u=rec.front(),rec.pop(); t[u].f=f; t[u].val=X; t[u].w=t[u].siz=1; LS=RS=0; if(f)t[f].ch[X>t[f].val]=u; }else{ ++t[u].w; ++t[u].siz; } splay(u,0); } void _delete(int X){ int pre=lower(X),last=upper(X); splay(pre,0);splay(last,pre); int u=t[last].ch[0]; if(t[u].w>1){ --t[u].w; --t[u].siz; splay(u,0); }else{ rec.push(u); t[last].ch[0]=0; t[u]=_NULL; } push_up(last); push_up(pre); } int Kth(int K){ int u=root; if(t[u].siz<K)return INF; while(K<=t[LS].siz||K>t[LS].siz+t[u].w){ //Attention if(K>t[LS].siz+t[u].w)//✔K-=t[LS].siz+t[u].w; K=K-t[LS].siz-t[u].w,u=RS; else u=LS; } splay(u,0); return t[u].val; } int Rank(int X){ find(X);int u=root; return t[u].val==X?t[LS].siz+1:-1; } #undef LS #undef RS } using namespace SPLAY; int main(){ _insert(INF);_insert(-INF); t[1].siz=t[2].siz=t[1].w=t[2].w=0; register int opt,x,n; scanf("%d",&n); while(n--){ scanf("%d%d",&opt,&x); switch(opt){ case 1: _insert(x); break; case 2: _delete(x); break; case 3: printf("%d\n",Rank(x)); break; case 4: printf("%d\n",Kth(x)); break; case 5: printf("%d\n",t[lower(x)].val); break; default: printf("%d\n",t[upper(x)].val); break; } } return 0; }
//luoguP3391 #include<iostream> #include<queue> using namespace std; const int N=1e6,INF=0x7fffffff; struct TREE{ int f,ch[2],tag,siz,val; }t[N]; int root,n,m,tot=0; #define LS (t[u].ch[0]) #define RS (t[u].ch[1]) void push_down(int u){ if(!t[u].tag)return; t[u].tag=0; t[LS].tag^=1; t[RS].tag^=1; swap(LS,RS); //swap in two numbers (ch[0] & ch[1]) } void push_up(int u){ t[u].siz=t[LS].siz+t[RS].siz+1; } void connect(int son,int f,int rel){ t[f].ch[rel]=son; t[son].f=f; } void rotate(int X){ int Y=t[X].f,Z=t[Y].f; int X_pos=X==t[Y].ch[1], Y_pos=Y==t[Z].ch[1]; connect(t[X].ch[X_pos^1],Y,X_pos); connect(Y,X,X_pos^1); connect(X,Z,Y_pos); push_up(Y); push_up(X); } //splay之后,因为该节点包含区间不变, //所以tag不变,Push_down会导致超时 void splay(int X,int goal){ while(t[X].f!=goal){ int Y=t[X].f,Z=t[Y].f; if(Z!=goal) (X==t[Y].ch[1])^(Y==t[Y].ch[1])? rotate(X):rotate(Y); rotate(X); } if(!goal)root=X; } int Kth(int k){ int u=root; while(true){ push_down(u); //Must if(k<=t[LS].siz) u=LS; else if(k>t[LS].siz+1) k-=t[LS].siz+1,u=RS; else return u; } splay(u,0); return u; } void split(int l,int r){ int L=Kth(l),R=Kth(r+2); splay(L,0);splay(R,L); int u=t[root].ch[1]; u=LS; t[u].tag^=1; } void insert(int x){ int u=root,f=0; while(u)f=u,u=t[u].ch[x>t[u].val]; u=++tot; t[f].ch[x>t[f].val]=u; t[u].f=f; t[u].siz=1; t[u].val=x; if(!root)root=u; splay(u,0); } void Make_str(){ insert(INF);insert(-INF); t[1].siz=t[2].siz=0; for(int i=1;i<=n;++i) insert(i); } void Mid_Root(int u){ push_down(u); if(LS)Mid_Root(LS); if(t[u].val!=INF&&t[u].val!=-INF) printf("%d ",t[u].val); if(RS)Mid_Root(RS); } int main(){ freopen("input.in","r",stdin); freopen("output.out","w",stdout); scanf("%d%d",&n,&m); int l,r; Make_str(); while(m--){ scanf("%d%d",&l,&r); split(l,r); }Mid_Root(root); return 0; }
完结散花!
就是完结了啊看什么看。
你学会了没呀QAQ
鸣谢列表
@scPointer 讲解了关于rotate操作中三条连边的理解问题
@BigYellowDog 提出建设性意见(大雾)
@CYJian 在我当初学习splay的时候提供了很大的帮助并讲解了关于哨兵节点的一些内容

