蒙特卡洛积分-重要性采样原理及其应用

我自己是数学菜逼，所以我在学习数学之类的内容的时候，我基本上会去找视频看，虽然视频比较耗时间，但数学真的很难，没办法，菜逼一个。好在在b站上找到一位数学老师有这个视频讲解，真的救命呀！！！放下视频链接https://www.bilibili.com/video/BV17D4y1o7J2?p=1&vd_source=4451d7e9f1ccf3c1318002d60666d680。下面记录一下笔记。

---

蒙特卡洛积分主要原理是通过随机抽样来估算。假设我们有一个概率密度（分布）函数如下，是某学校女生身高的分布

 

假设我们想算身高平方的均值，f(x)是概率密度函数，g(x)=x²,身高平方的均值也就是

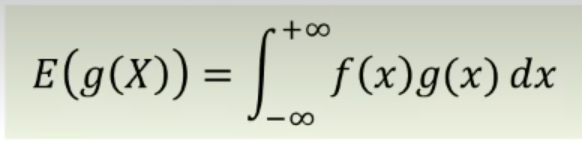
但是因为这个积分解析式不一定能解出来，我们可以在概率密度函数的分布中抽取样本X，也就是在某学校女生中抽样，然后计算g(X)，进而算术平均

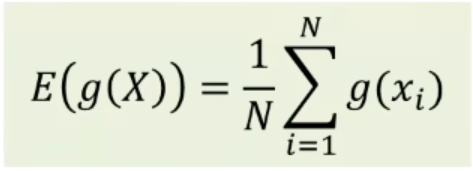
但在数学中如何找到可以服从概率密度分布的样本呢，这里需要用到累积分布函数

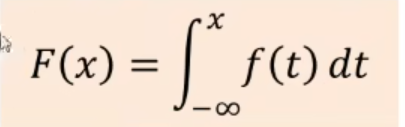
由于累积分布函数从0到1，它的函数图像如下

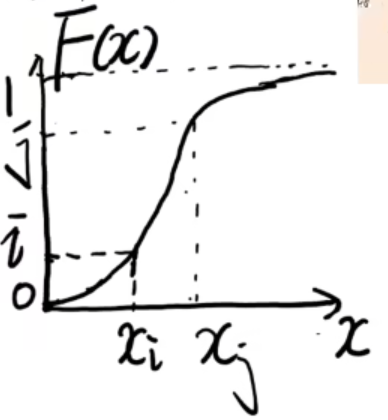
我们在累积分布函数的纵坐标上随机取一个数i，找到它在横坐标上对应的值x_i，这个x_i就是符合概率密度函数的样本了，xi的求解也就是累积分布函数的逆函数了，这个也就是重要性采样了

到这里就可以解出来了。

我们经常看到在图形学中的渲染公式中那一长串的被积函数，然后就突然变成了一长串除以pdf了，那这个除以pdf是怎么来的呢？

假设我们要求f(x)在(a,b)上的定积分（面积），g(x)是一个概率密度函数，我们可以把这个式子变形

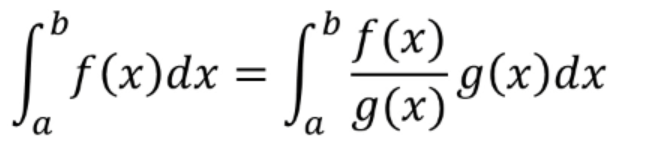
我们可以把f(x)/g(x)看成一个整体z(x)，那这样不就是对应我们前面的列子了吗，就相当于变成了求z(x)的均值了，然后我们就可以采样得出结果了，有一些细节就是概率密度函数的积分为1，也就是

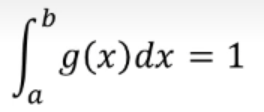
然后我们的式子就变成这样了

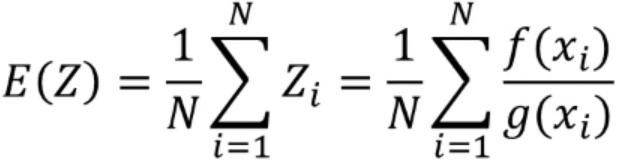
 对，这样就变成了我们经常看到的除以pdf的那种样子了。

下面举一个实例，求解y=x²在(0,2)之间的面积，用定积分的解析式很好求，结果是8/3。但这里用蒙特卡洛重要采样来解积分。首先pdf是随便的，这里取概率密度函数p(x)=3/8*x²，p(x)在(0,2)上的积分为1，这是必须条件。尽量贴合原积分函数，然后我们求出累积分布函数P(x)=x³/8，按照上面的讲解我们求出累积分布函数的逆函数P^-1(x)=2*x^1/3，在累积分布函数的逆函数上我们的自变量范围就是(0,1)。代码中只采样了一个点，但得到的结果还是比较准确的

#include <iostream>
#include <random>
#include <iomanip>

double random_double(double min, double max)
{
    // 使用rd来生成一个真正的随机数生成器
    std::random_device rd;

    // 使用该随机数生成器初始化Mersenne Twister引擎
    std::mt19937 engine(rd());

    // 创建一个分布，在min和max之间均匀分布
    std::uniform_real_distribution<> distrib(min, max);

    // 生成一个均匀分布的随机数
    return distrib(engine);
}

inline double pdf(double x)
{
    return 3 * x * x / 8;
}

int main()
{
    int N = 1;
    auto sum = 0.0;
    for (int i = 0; i < N; i++)
    {
        //这里就是用累积分布函数的逆函数来求解符合概率密度函数的分布
        auto x = 2*pow(random_double(0, 1), 1.0 / 3.0);
        sum += x * x / pdf(x);
    }
    std::cout << std::fixed << std::setprecision(12);
    std::cout << "I = " << sum / N << '\n';
}

结果如下：