纹理映射

三维模型中每个三角形的顶点都可以找到在贴图中的对应点

 

重心坐标：已知三角形三个顶点，通关重心坐标的方法，在三角形内进行平滑的过度，使得三角形内每个点都有相对应的值。

 

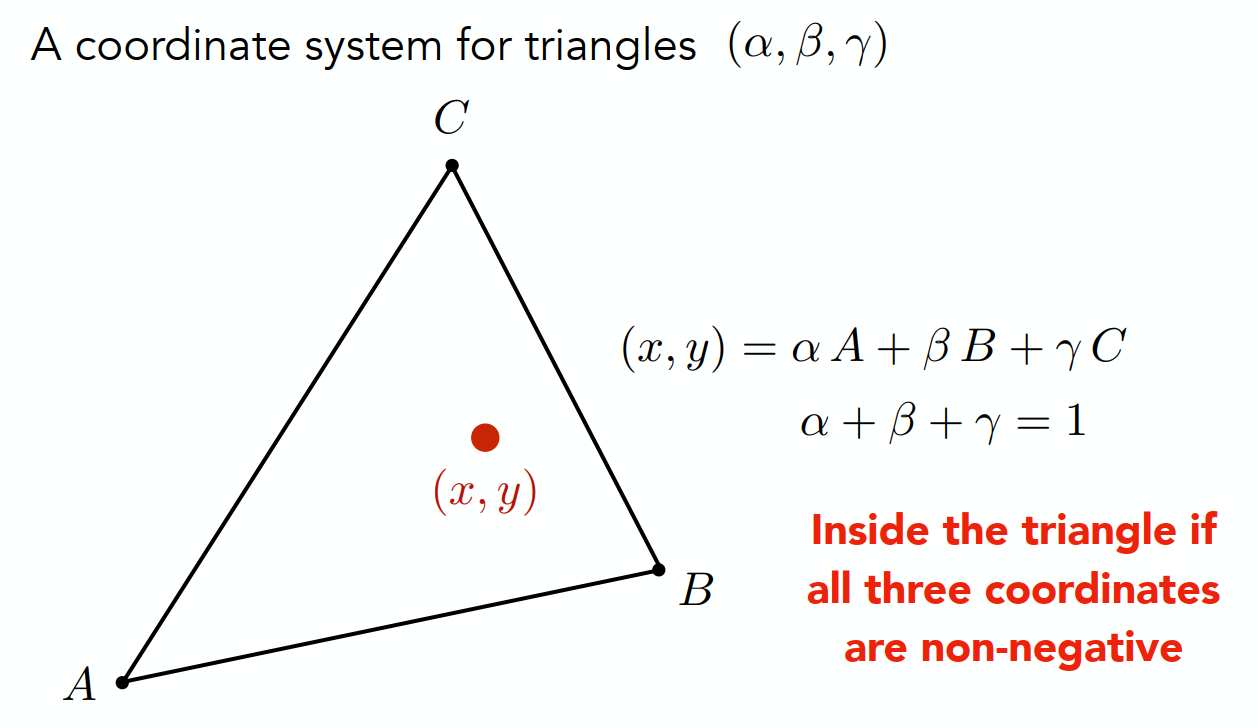
当α+β+γ=1时，点(x, y)在三角形所在的平面上，当且α>=0,β>=0,γ>=0,点(x, y)在三角形内。

重心坐标也可以通过面积比计算。

 

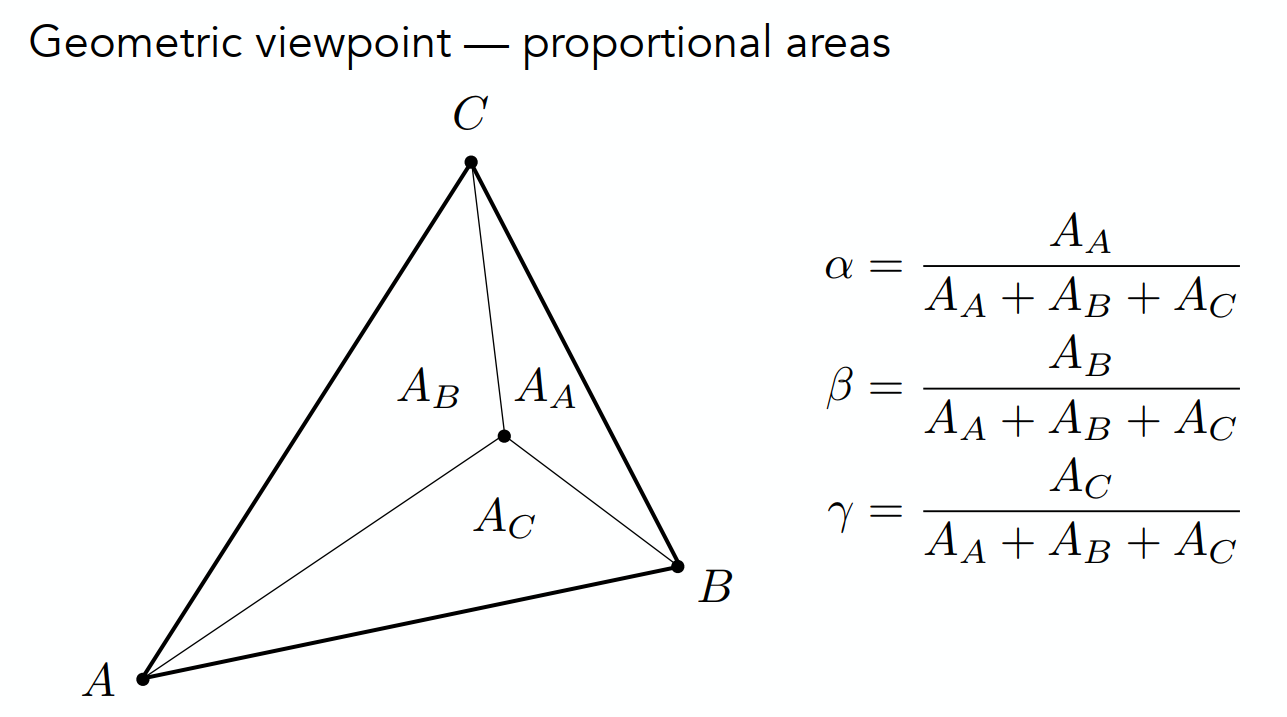
也可以通过公式计算

 

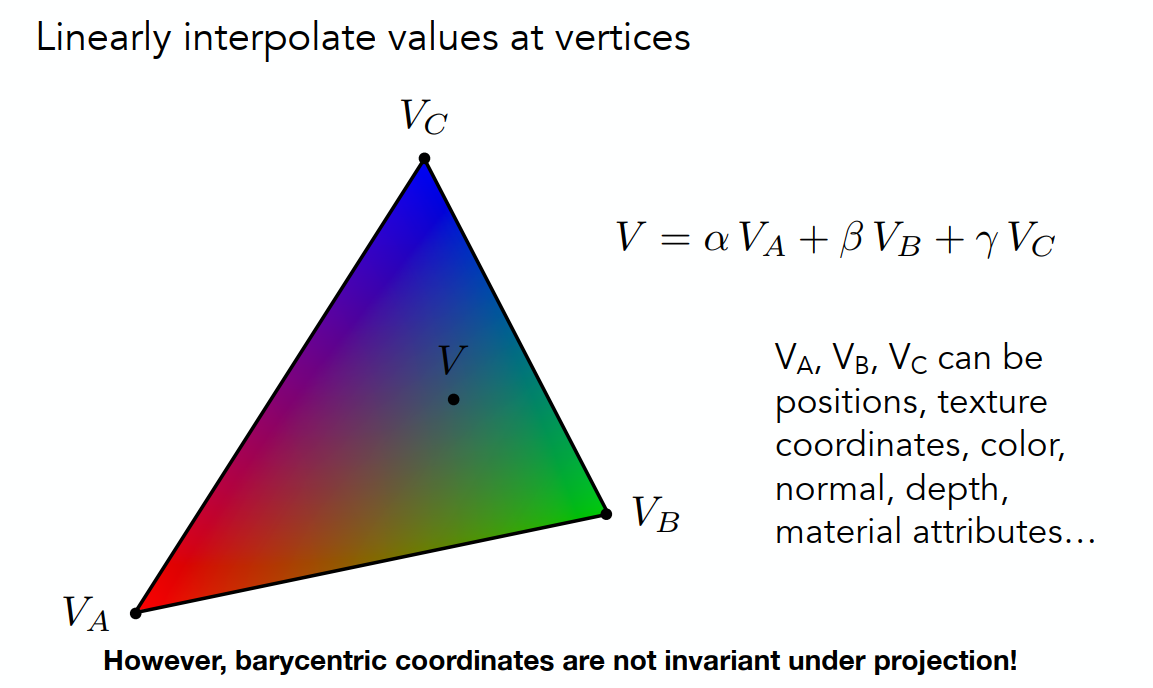
通过重心坐标来计算三角形内部的颜色过度，重心坐标在投影变换后就会不符合，即需要先计算三维空间下的重心坐标，然后进行投影变换

 

 

 

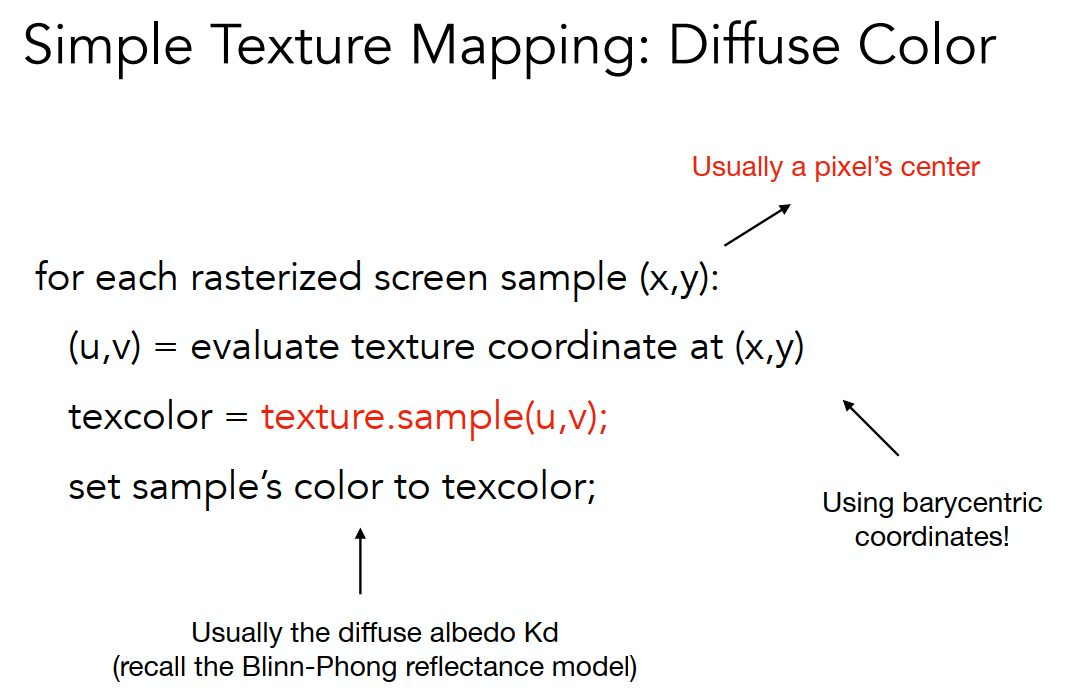
贴图映射应用在漫反射系数上，通过插值来计算相对应的(u,v)

 

 

 

 但会有一系列的问题，当屏幕像素过大，贴图过小时，屏幕像素就会对应到贴图中的小数部分，在四舍五入后，就会造成很多像素点对应到同一个

贴图像素中，从而造成了模糊的结果。

 

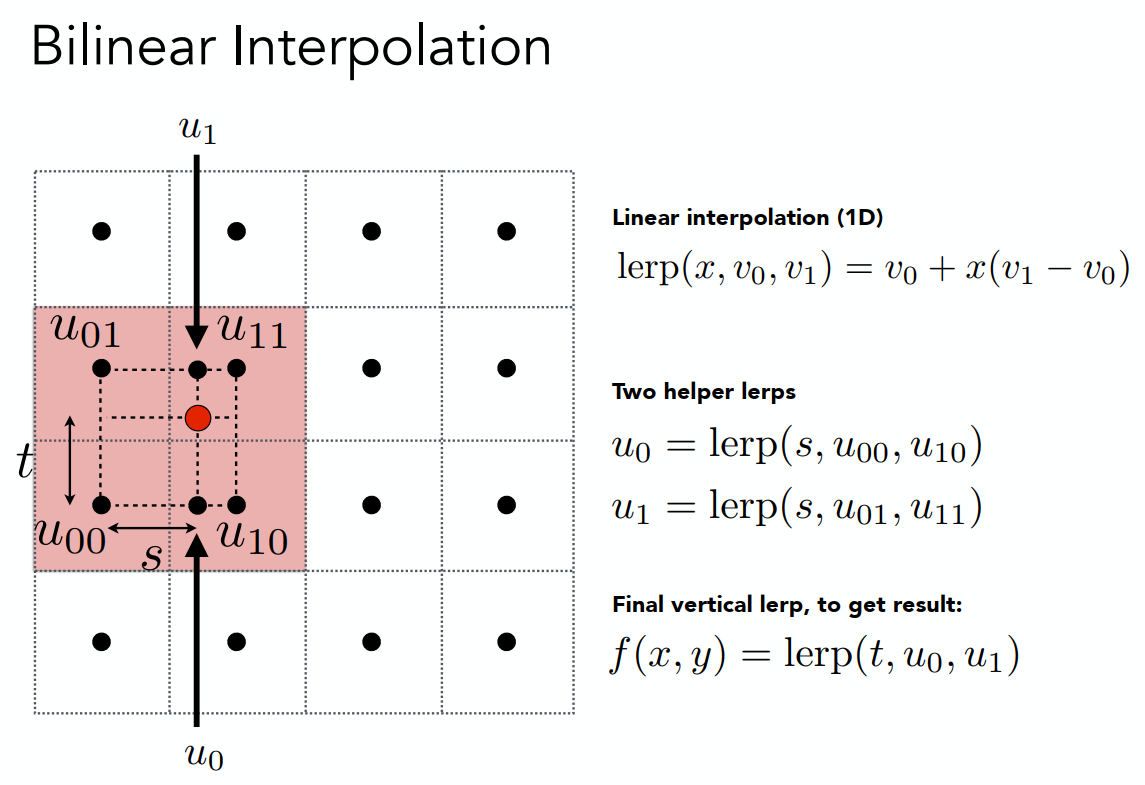
使用插值的方法来解决，双线性插值，让一个点和它周围的四个点相关，先在上下边计算插值，然后再计算竖直边插值（当然先竖直再水平也可以）

 

 

 

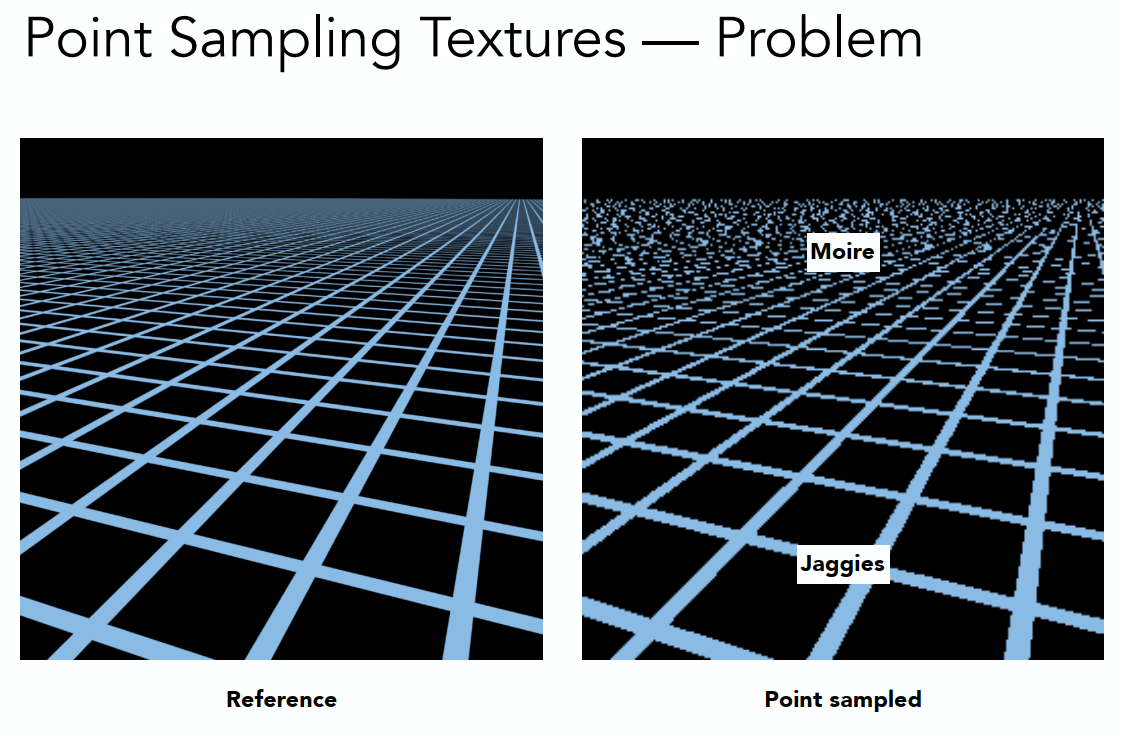
在贴图过大时，会造成更严重的问题，远处会出现模糊，近处会出现锯齿

 

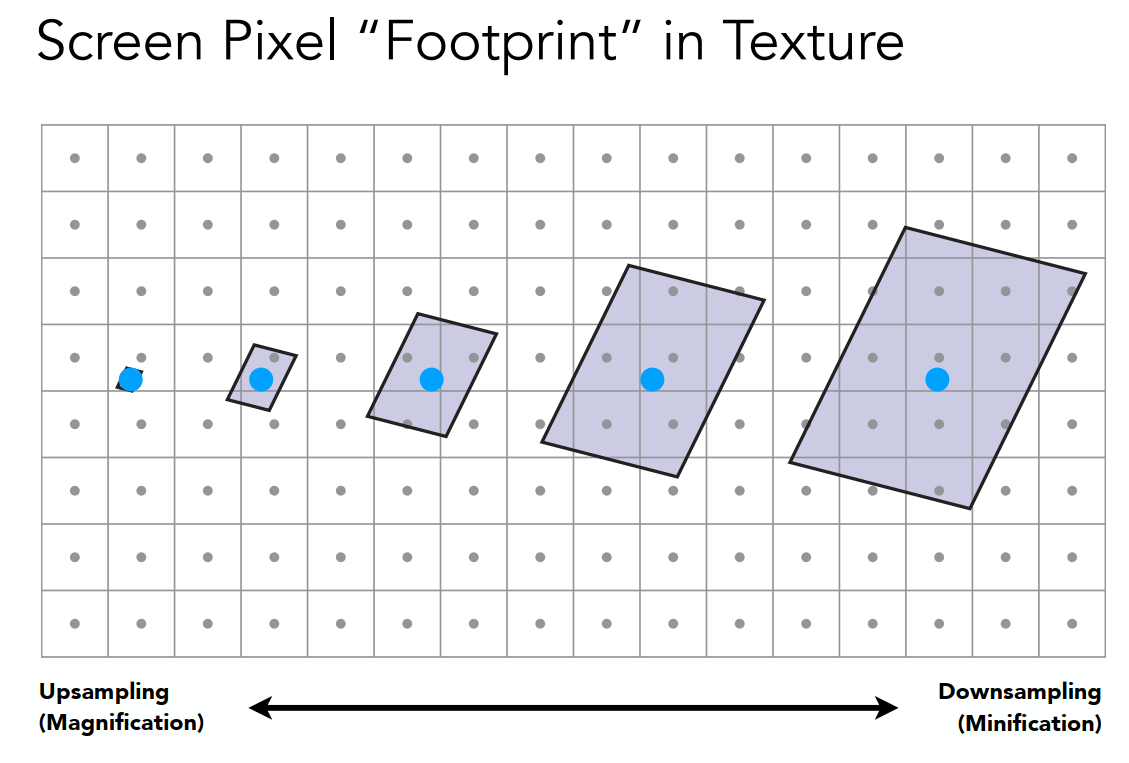
原因是因为在远处时一个像素所代表的图贴范围太大

 

 

 

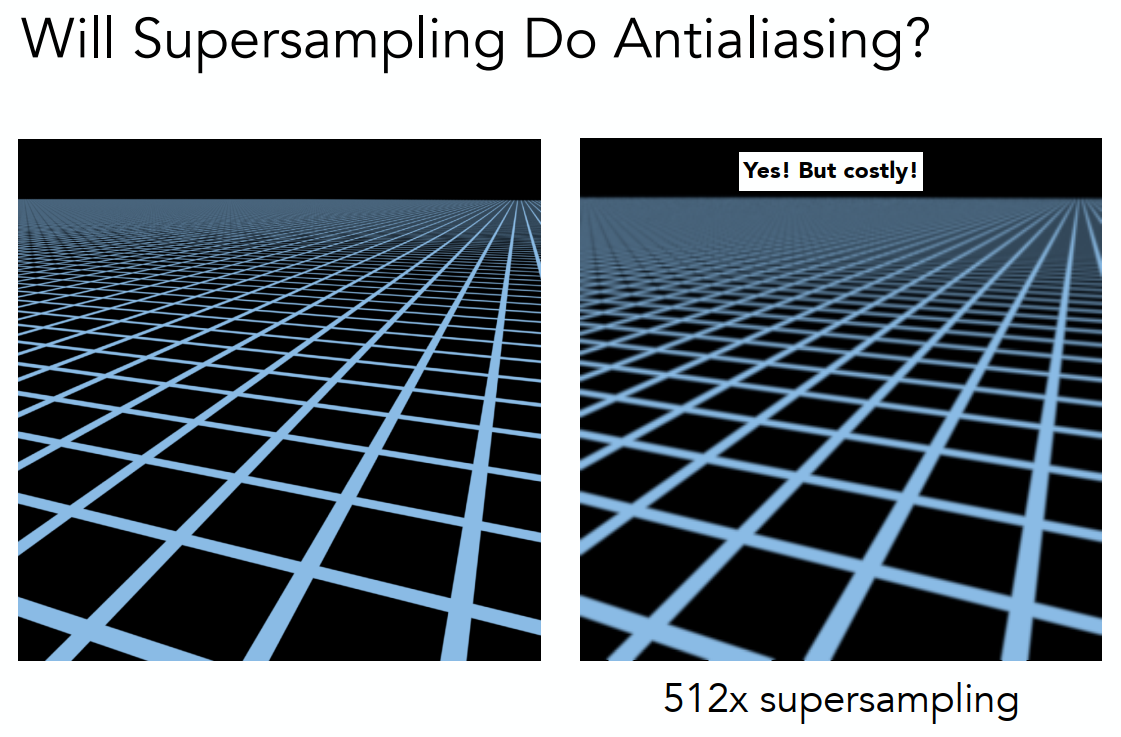
 可以使用超采样的方法来解决，即也是在一个像素内划分出很多点，然后算出贴图范围，再求平均，但这种方法开销较大

 

 

使用Mipmap的方法来解决，它通过对贴图范围的缩小来解决，即把像素大小不断缩小，到最后的1X1。Mipmap是对正方形的快速近似查询。

 每一个图都是上一个图一半的大小，所以总共的内存占用就是等比数列求和，最后也就是4/3的大小

 

 

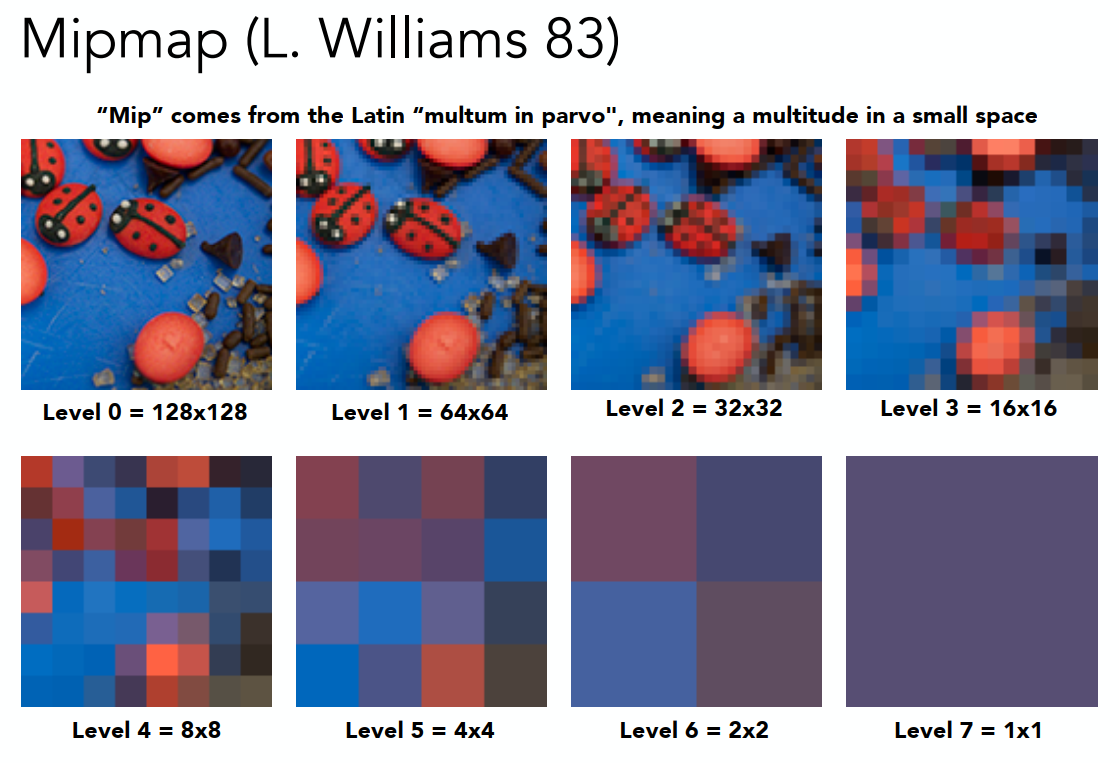
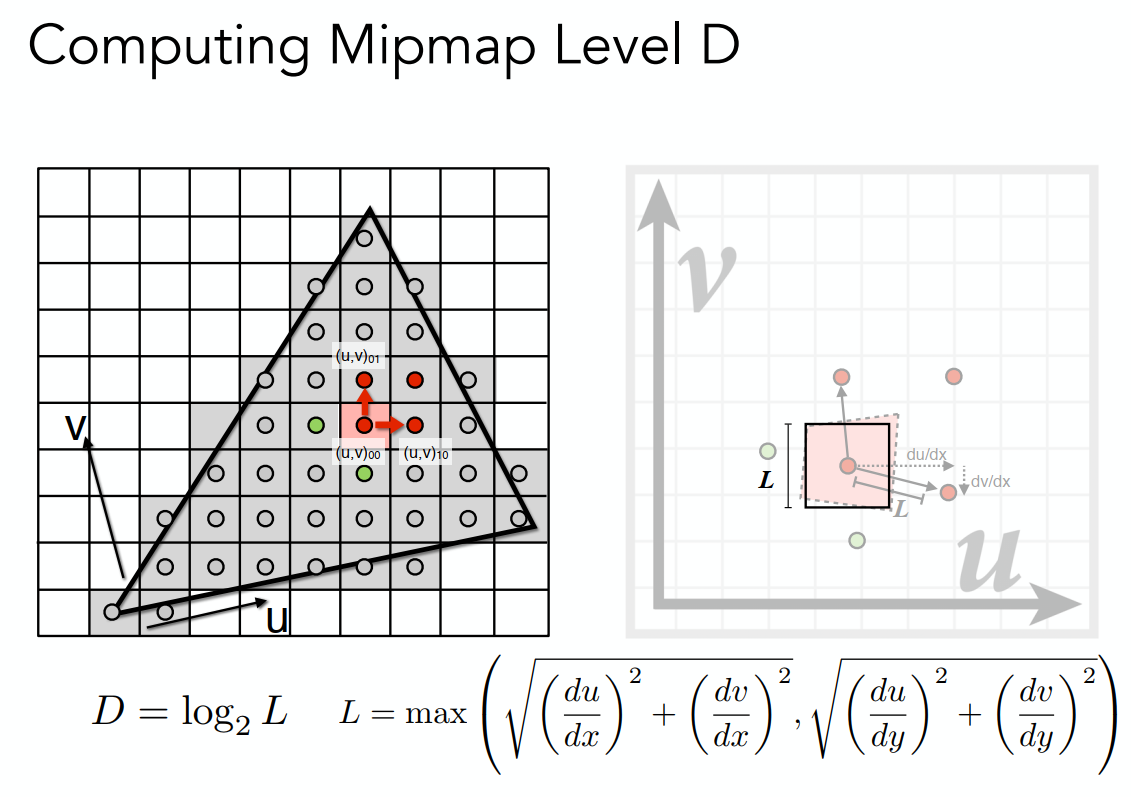
在使用时，先获得像素对应的贴图大小，根据近似的正方形边长来查询对应的贴图大小

 

 

 

 

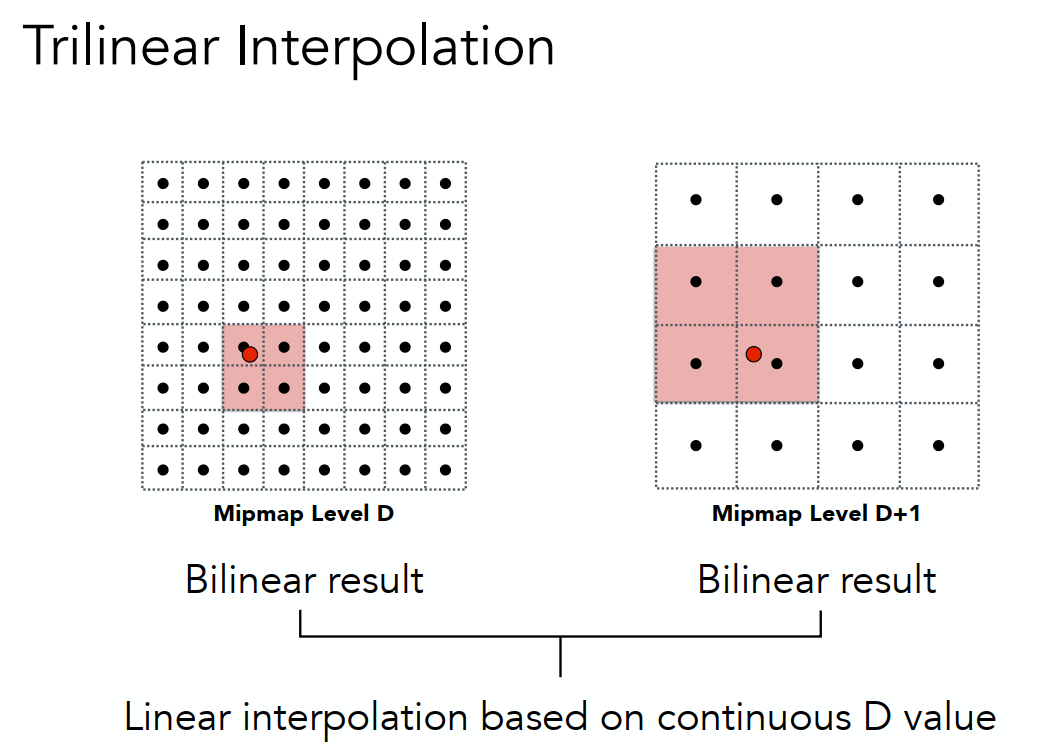
但第一层与第二层之间的过渡不平滑，需要在层与层之间进行插值

 

 

但Mipmap依然会造成问题，会在远处有重叠的现象

 

 

 

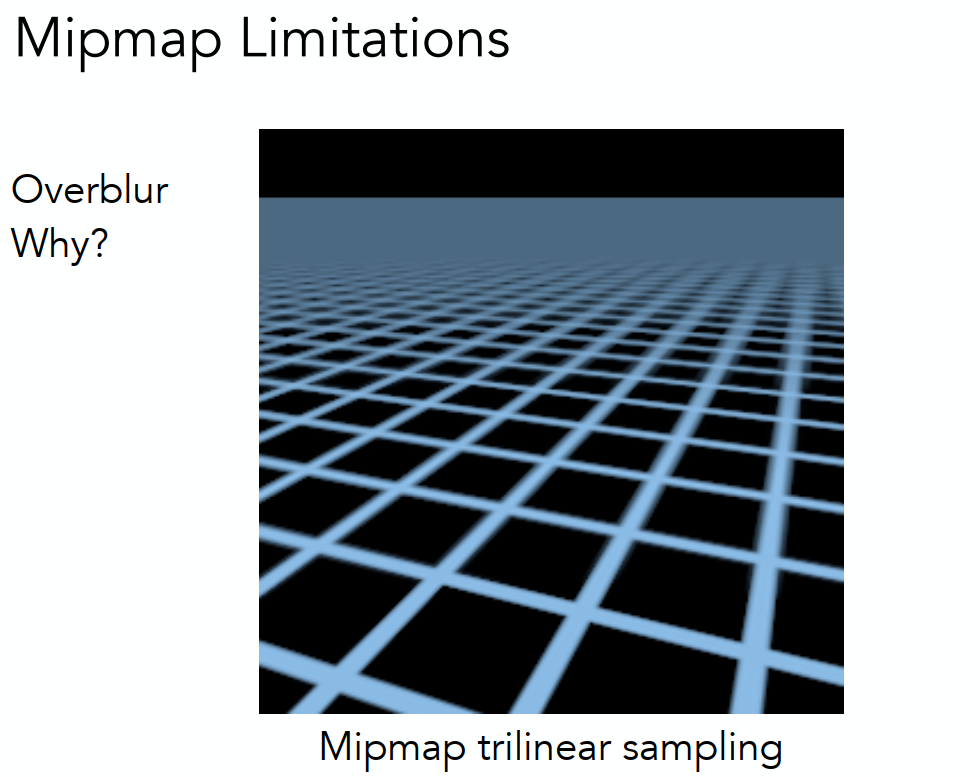
造成的原因是因为屏幕上的像素对应到贴图上的范围，并不一定近似是正方形或者矩阵，而是一些不规则的图形

 

 

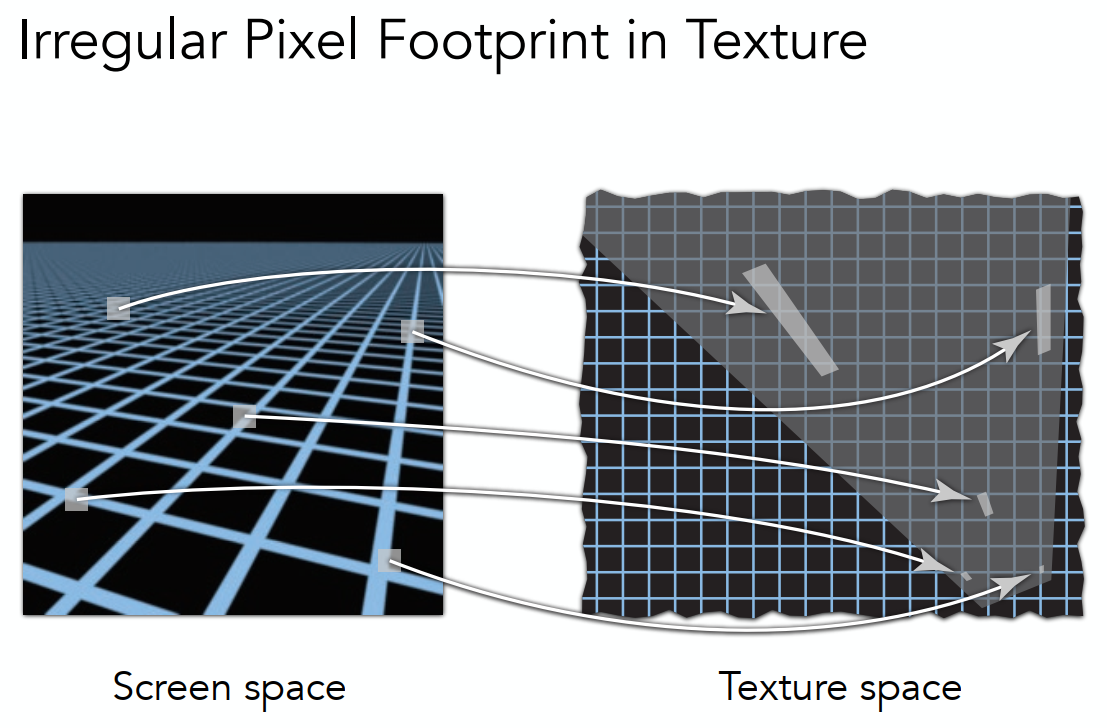
使用各项异性过滤来解决近似矩形范围的问题，

 

 

EWA过滤：使用椭圆来覆盖不规则图形，要多次查询，会降低性能