线性变换

缩放变换：用矩阵来表示变换

 

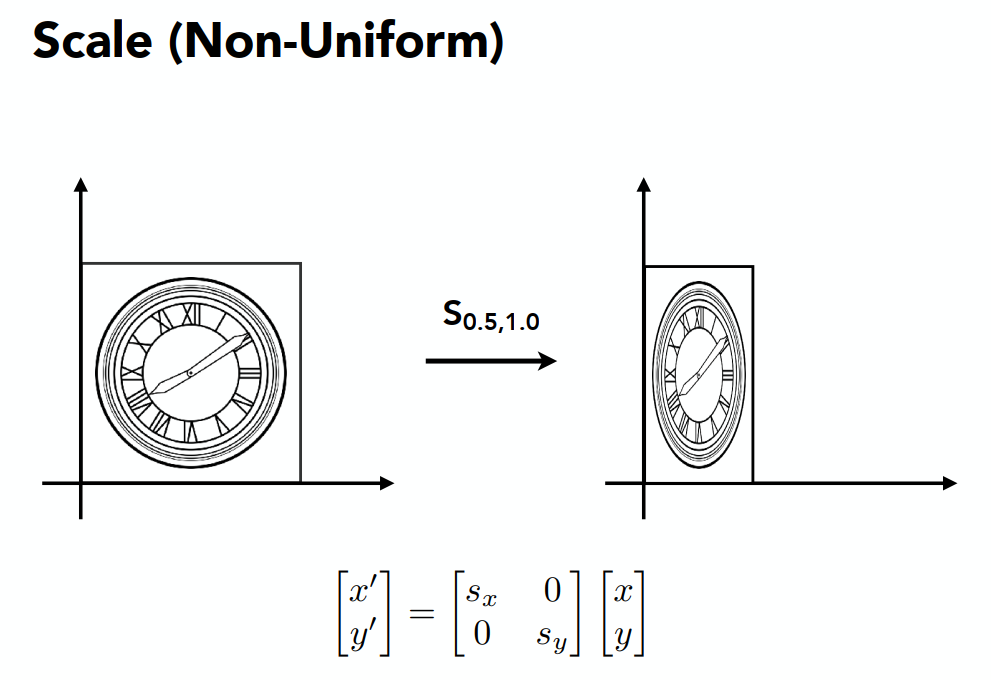
矩阵反射：即矩阵沿着某一个轴对称

 

切变变换：

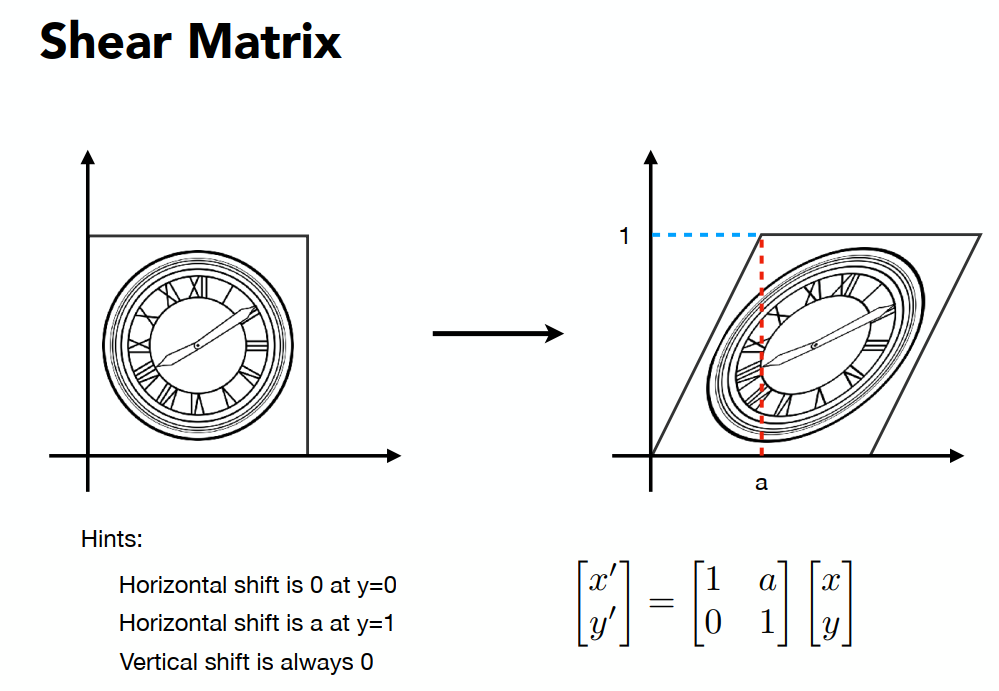
旋转变换：

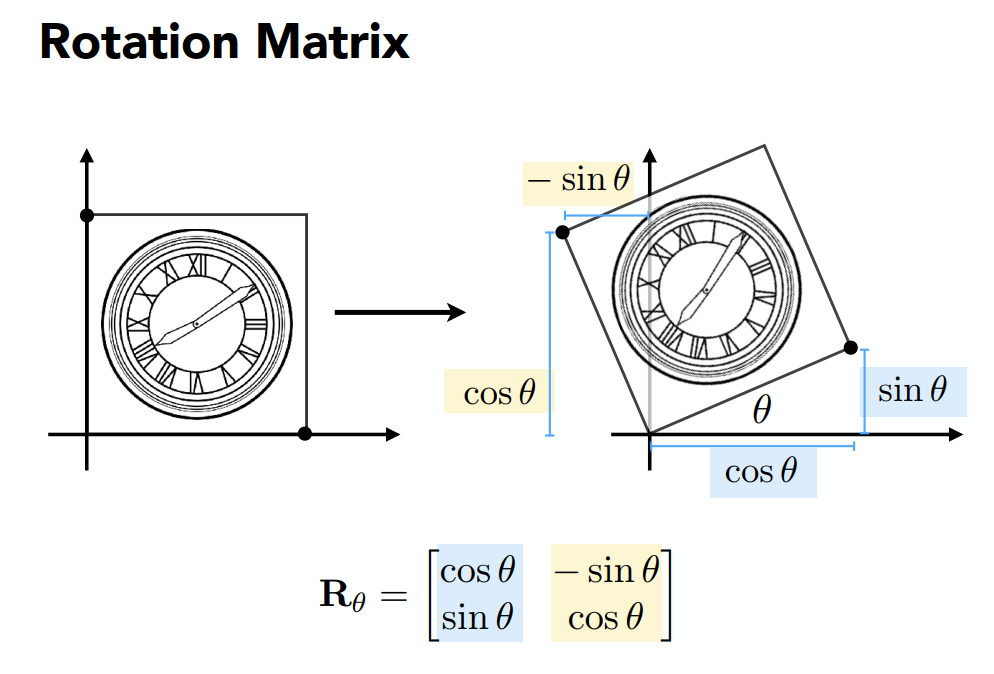
平移变换：平移变换需要在后面加上位移变换，此时的表达式就不是线性变换了，引入齐次坐标来解决这个问题

引入新的定义，把二维空间中的点和向量改变，在后面拓展一位，1结尾为点，0结尾为向量，然后对应的矩阵也要拓展，即可获得平移的线性变换。

把访射变换转换为齐次坐标，这时把旋转或者缩放加上平移放在一个表达式中，注意此时是先进行变换，再平移

 

 

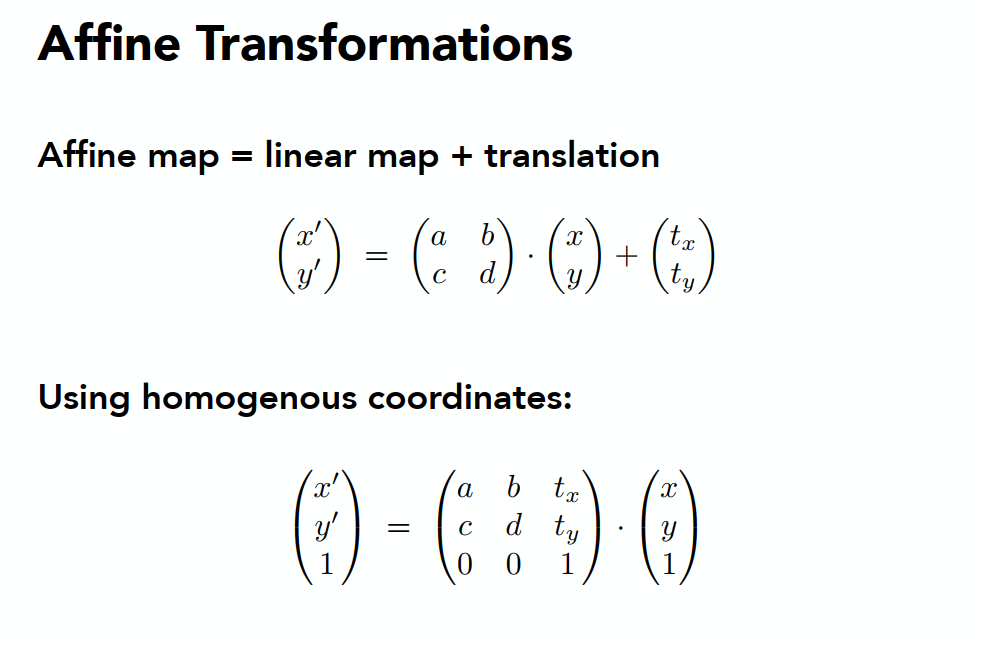
 最后把所有的变换都转变为统一的齐次坐标下：

 

 

 逆变换：

 

 

 组合变换：

 

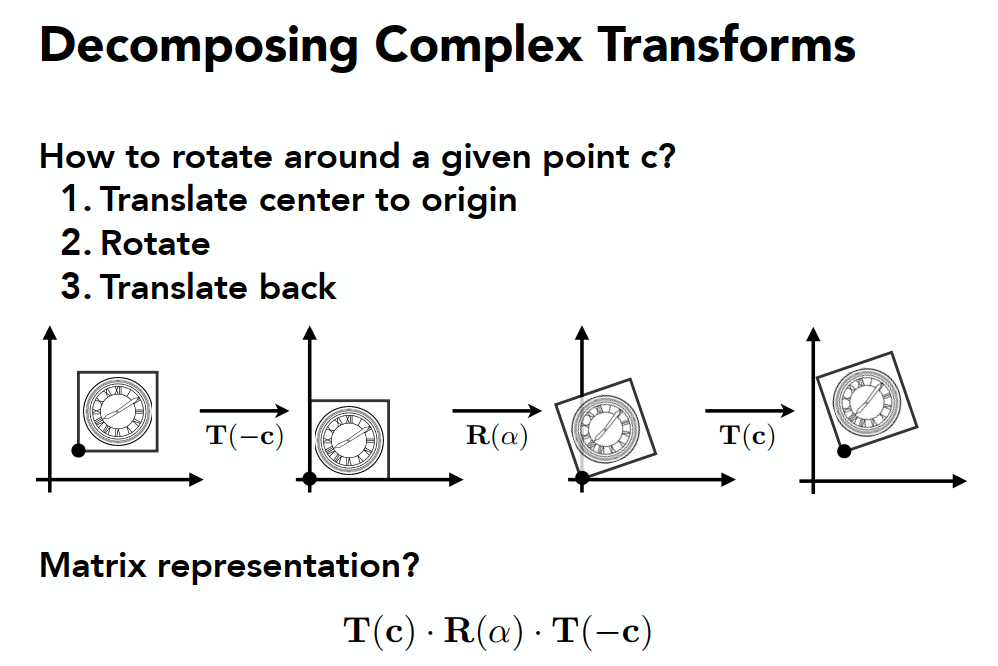
 三维变换参考二维变换：

 旋转矩阵的逆矩阵等于转置矩阵：

 

 

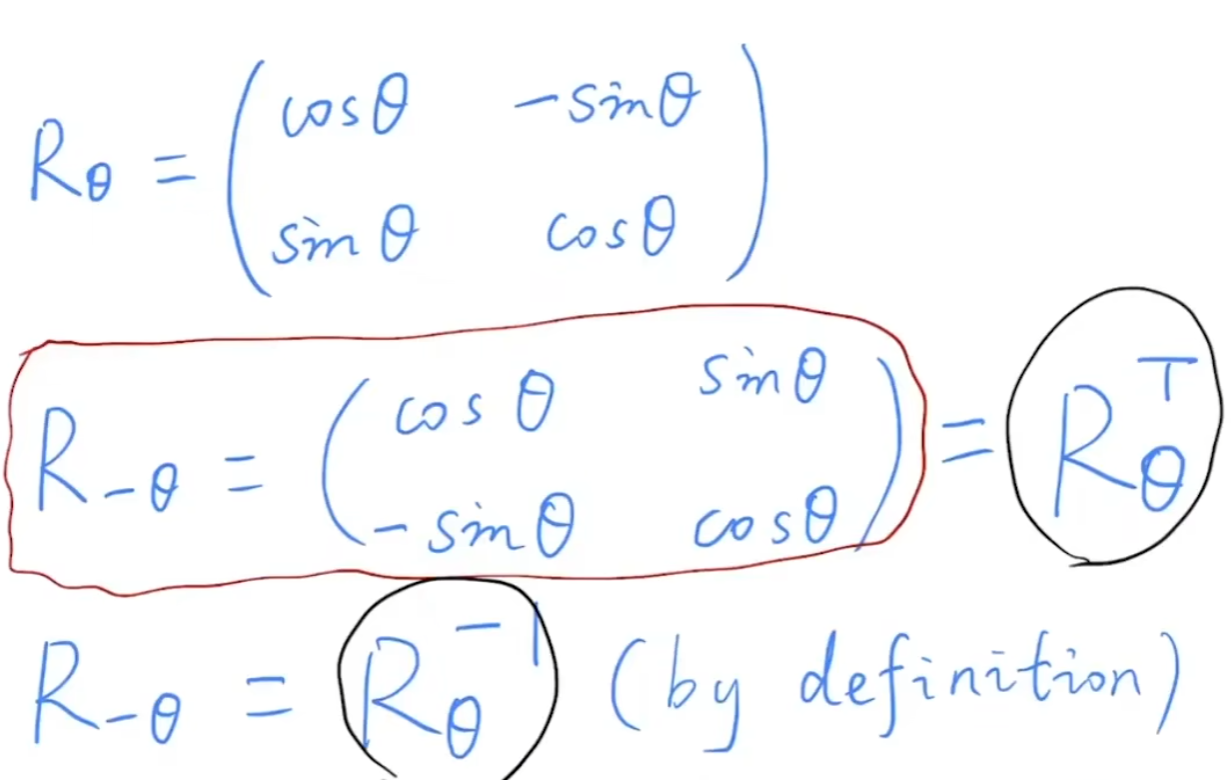
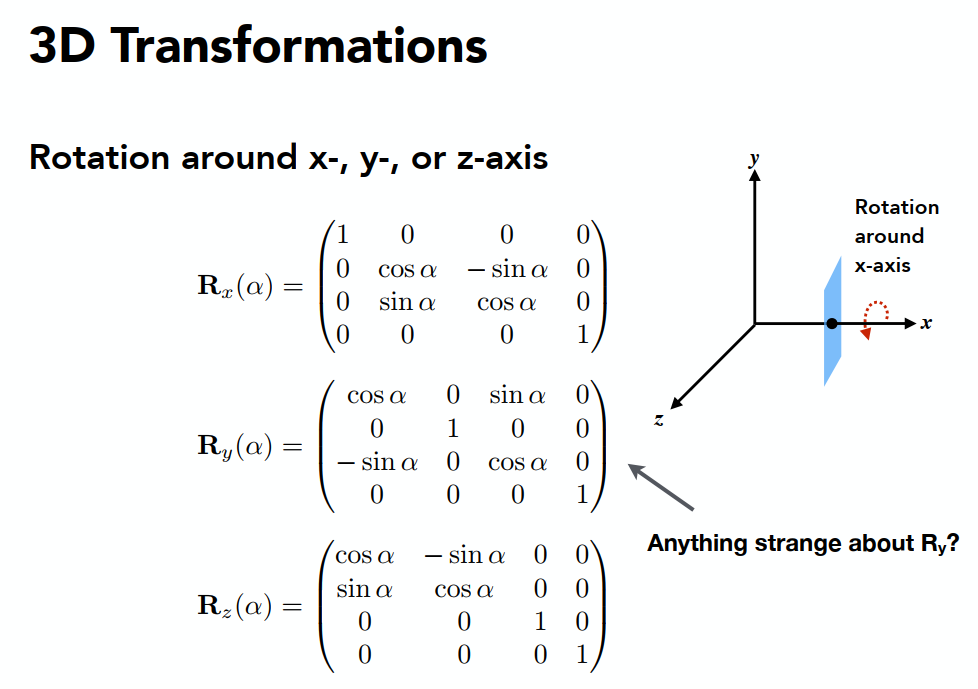
 三维变换矩阵：

 

x*y=z，y*z=x，绕y轴旋转时，因为y轴并不是x*z得到，而是由z*x得到，所以左下角和右上角互换。

 

 

 

 

 沿着任意轴和角度旋转的变换矩阵：