路径追踪
Monte Carlo Integration
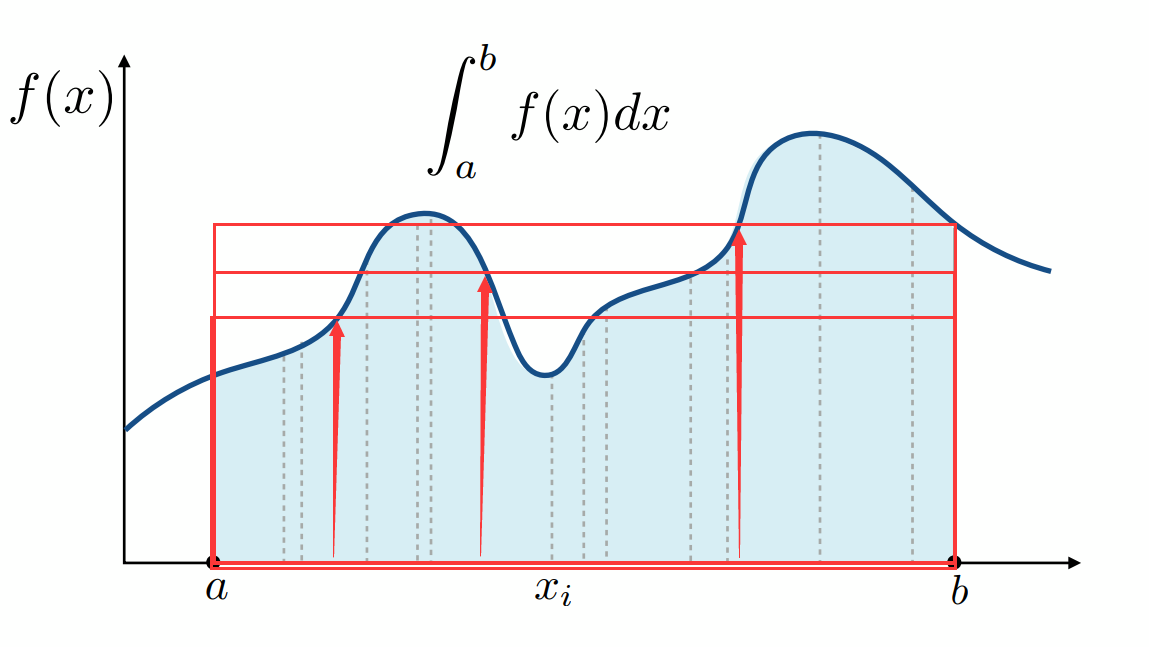
:蒙特卡罗积分,近似求定积分的一种方法,取某个点xi,对应的y值做矩形,此矩形近似等于定积分面积,然后取多次求平均
求出概率密度函数pdf,就可以解出定积分,一般使用平均采样,使得概率密度函数是常数,概率密度函数在自变量区间内对dx进行积分就是概率之和等于1。



此时上图中的FN就是开头提出的那种以矩形面积近似等于定积分的结果,b-a为矩形的宽,f(Xi)为矩形的高,然后加起来求平均。
下图就是蒙特卡罗积分求定积分的公式。

路径追踪
Whitted-Style Ray Tracing: Problem 1:
Whitted-Style的性质是镜面反射和折射,在粗糙表面会停止反射。
Whitted-Style Ray Tracing在镜面反射的物体表面上是对的,但在漫反射的(粗糙)物体表面上是错的,因为Whitted-Style的光线只会镜面反射和折射,而实际物体表面的光线是有漫反射的。此时当Whitted-Style Ray照射到粗糙表面就会发生反物理现象,
Whitted-Style Ray Tracing: Problem 2:
Whitted-Style Ray在照射到漫反射表面时会停止,直接进行着色计算,此时就会忽略物体与物体之间的漫反射光线。

而路径追踪就是为了解决Whitted-Style Ray Tracing的问题。
从渲染方程开始分析,因为渲染方程肯定是对的
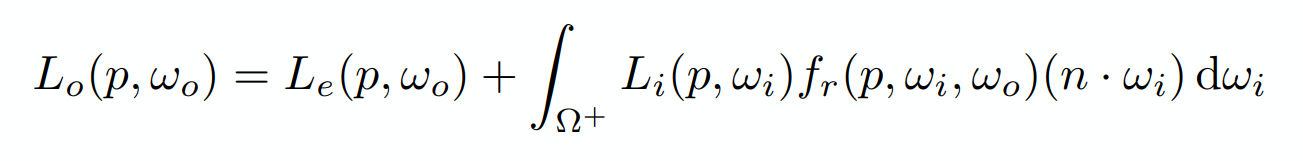
此时,我们需要解出右边的定积分。考虑在某一个点p的着色,p点的光照来源于光源或者漫反射光,先只考虑来源于光源的光,
入射光Li是从各方位的立体角wi入射进来,然后经过prdf反射出去,使用蒙特卡罗积分求解,首先需要知道解出pdf,由于是对
立体角wi进行积分的,对wi在各个方向平均取值,即pdf为常数,wi在半球方向上为2π,wi为定积分区间。即从0到2π。
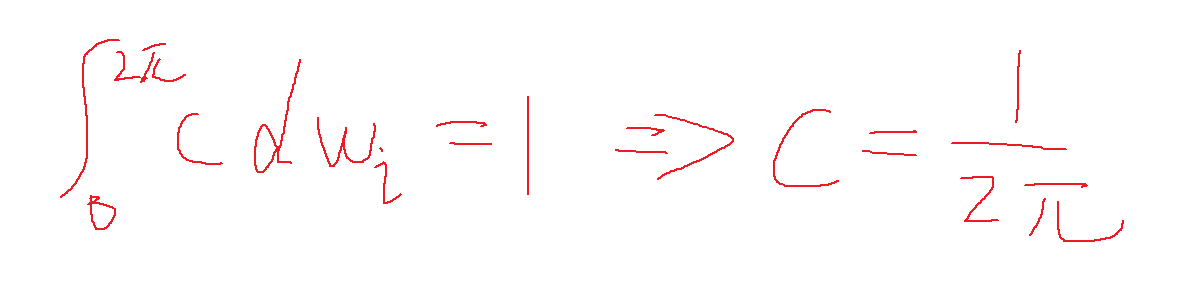


然后考虑从其他物体漫反射进来的光线,此时把p点作为摄像机,Q点作为着色点,也就是递归了
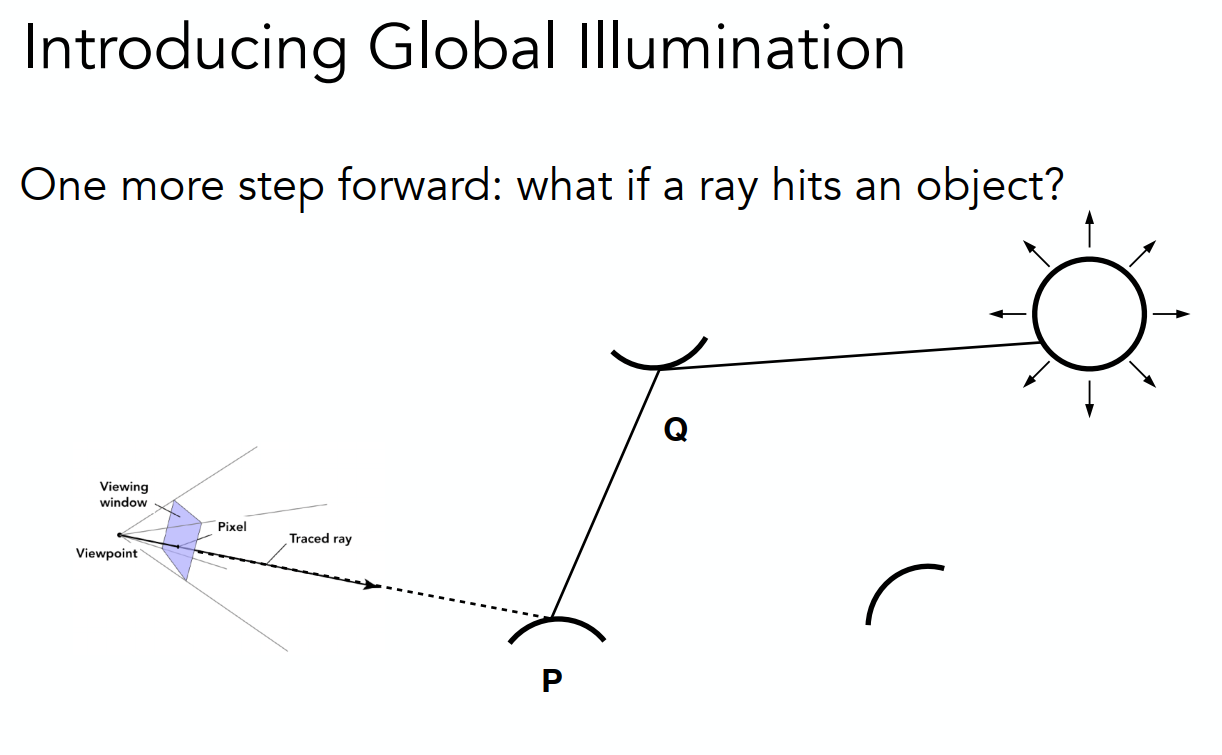

但此时会有第一个问题,在考虑一个点的着色时,我们会朝着各个方向来计算他们的光线,也就是说一根光线会转变成N个光线,然后在下一个点又会转变成N个光线,就是指数级爆炸了,为了解决这个问题,我们只能把N=1,这个时候就是Path Tracing了。


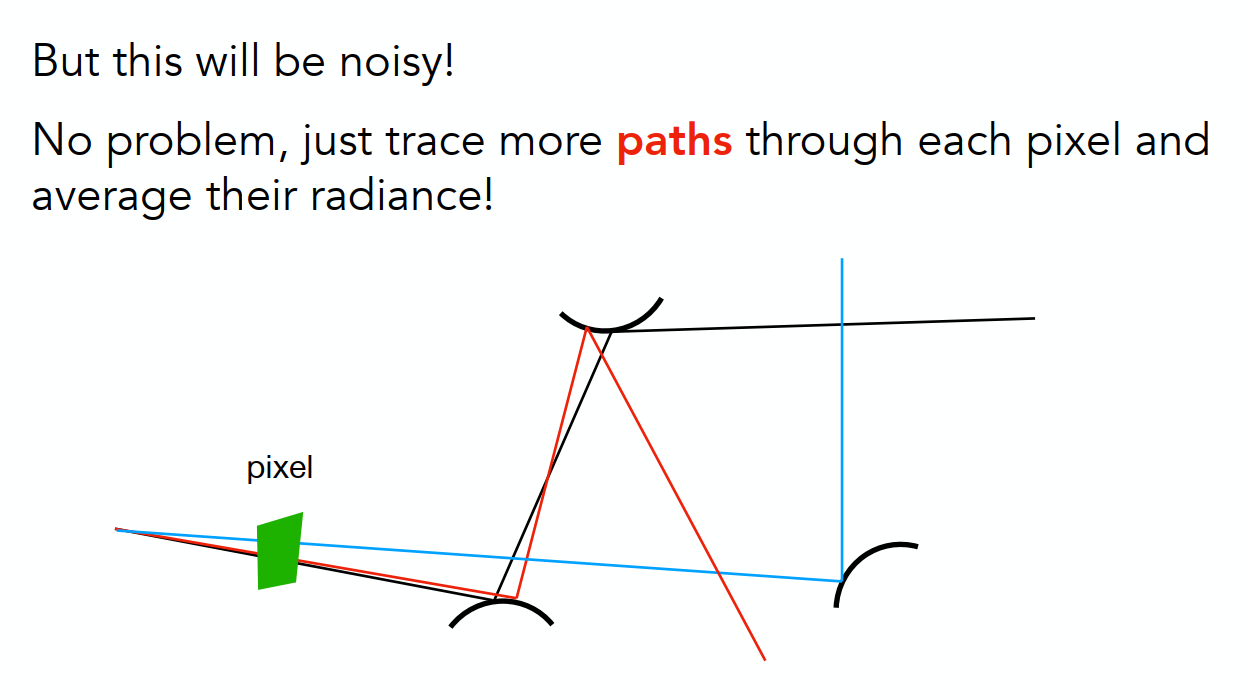
在实际操作时,从观测点向一个像素发出N跟光线,然后算出这N个光线的路径追踪后再求平均,即为该像素的着色结果,
此时也算是解决噪声大的问题。

第二个问题是上图中的代码停不下来,因为递归必须是要有停止条件的,在现实生活中的光线是会无限反弹的,但计算机不能模拟无限次反弹,
所以引进俄罗斯轮盘赌的概念来解决此问题,即每一根光线有一定的概率能反弹出去,反之就是不能弹射出去。


这个时候还有一个问题,当我们在一个像素上的采样率比较低的时候噪声会比较大,虽然高采样率会解决这个问题,但造成了性能的开销,我们希望
低采样率时也能有一个低噪音的效果。

原因是因为pdf的采样是在单位半球上对各个方向采样的,从单位球上向各个方向发出光线,但并不是每根光线都能达到光源上,
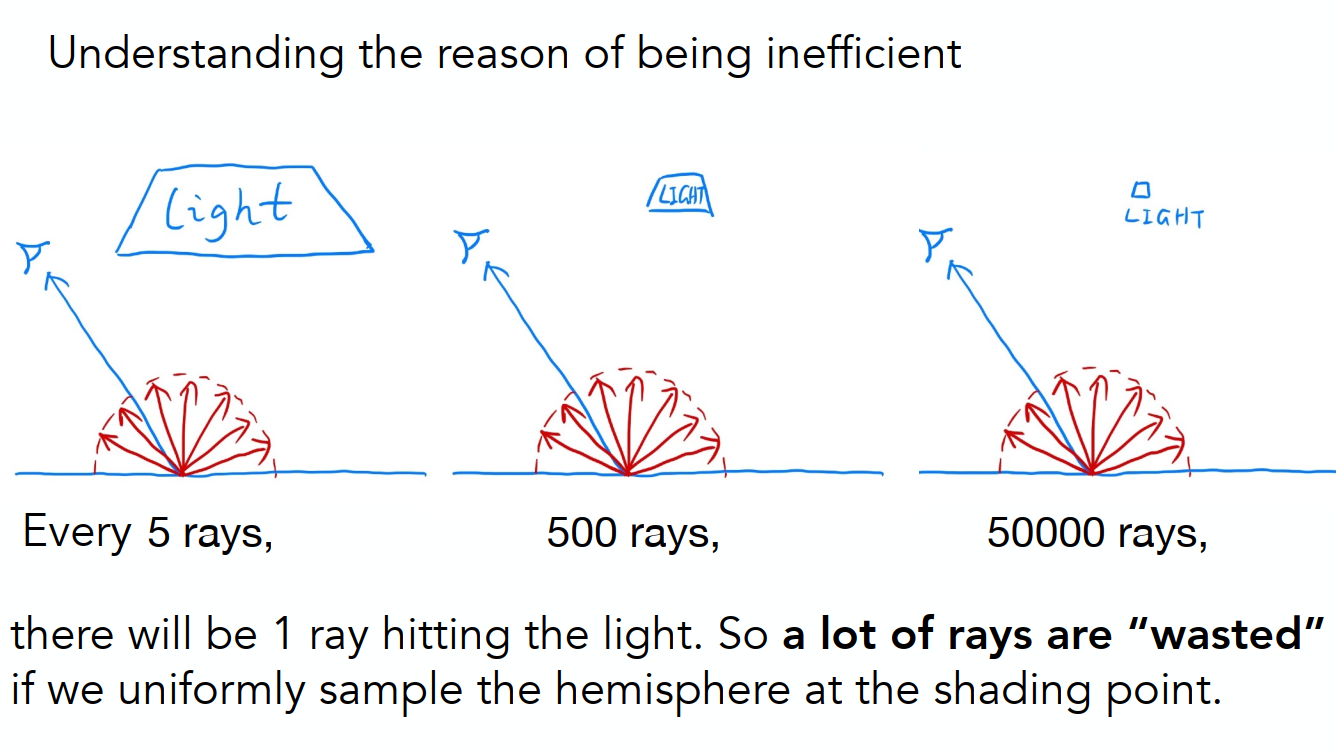
根据蒙特卡洛的原理,pdf并不是固定的,改变pdf来改变上面的情况,此时我们在光源上采样,就保证了每根光线都可以到达光源上。
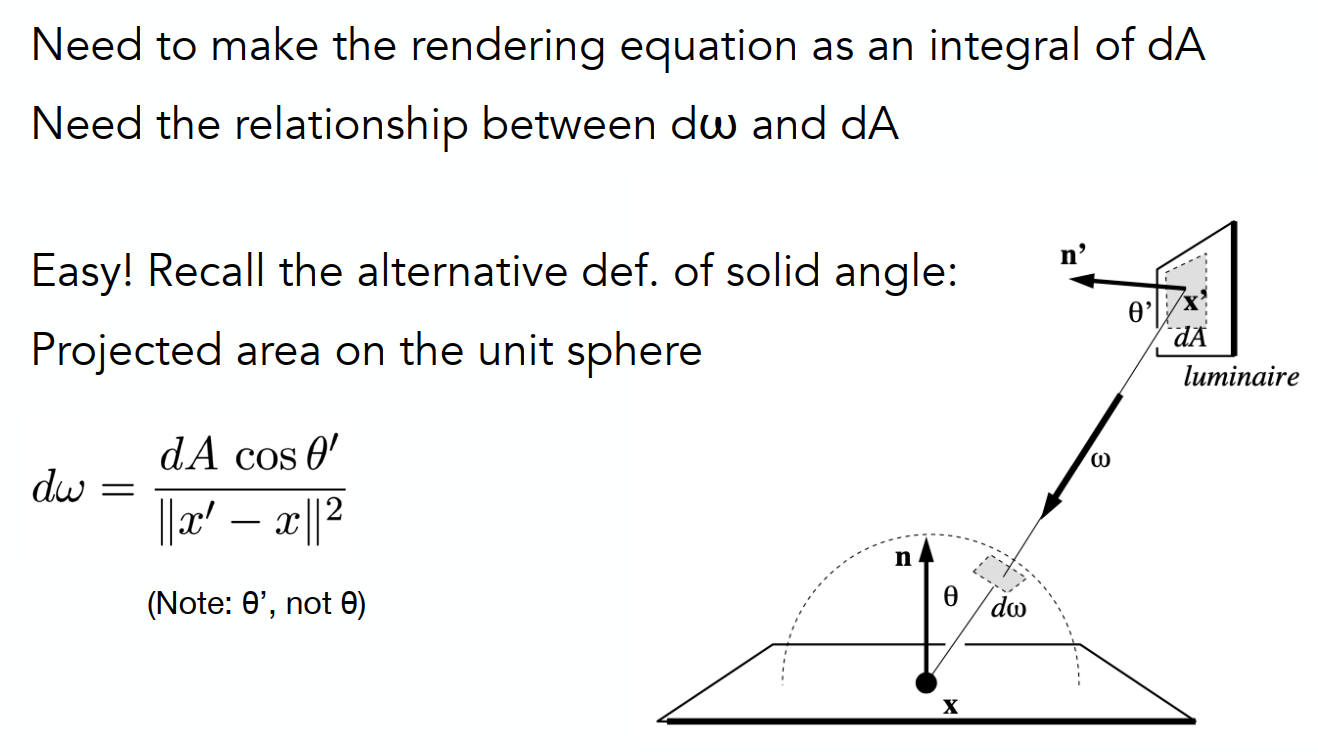
但因为采样是在光源上,积分是在单位球的立体角上,就不符合蒙特卡洛积分

这时我们把dA转换成dw
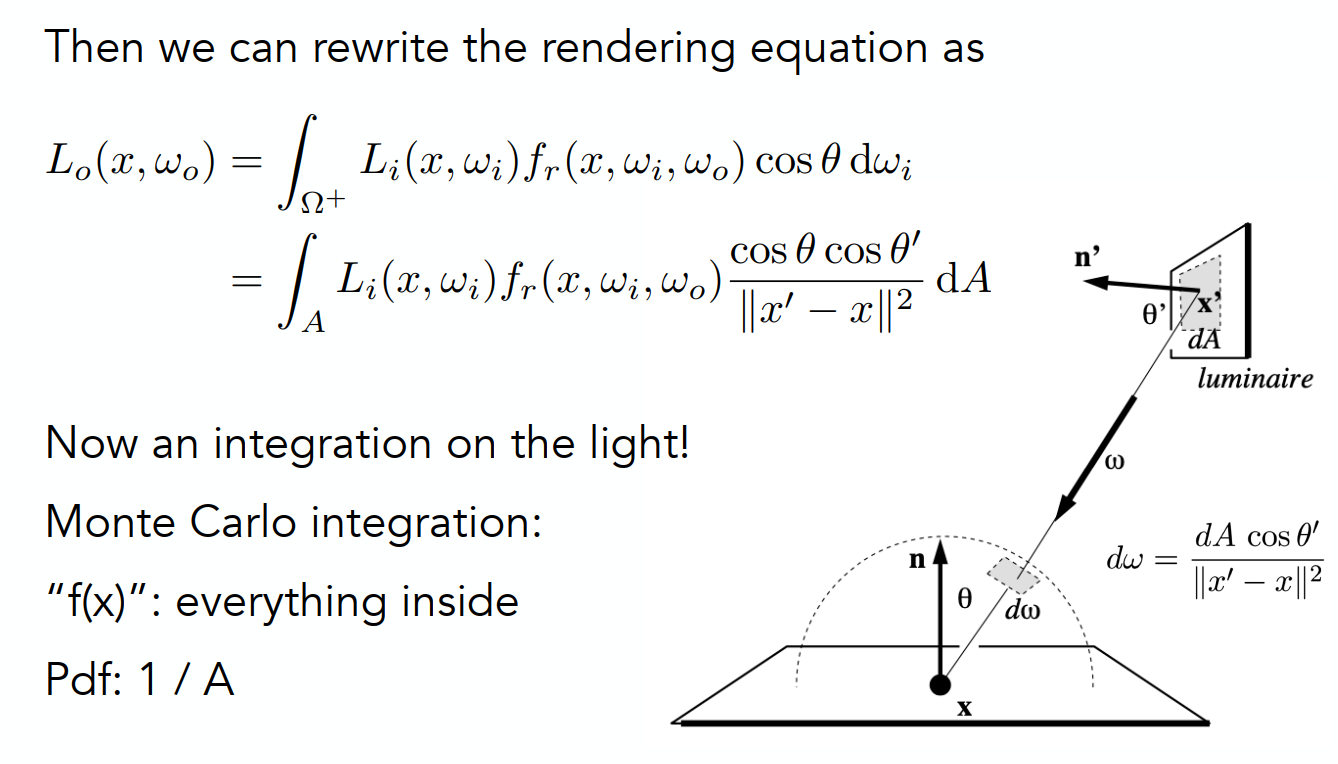
得到最终的结果

还有一个小问题就是从着色点到光源之间是否有遮挡物,从着色点发出一条光线到光源,检查是否能不能直接到达光源





