第七章学习心得
第七章 查找
思维导图:
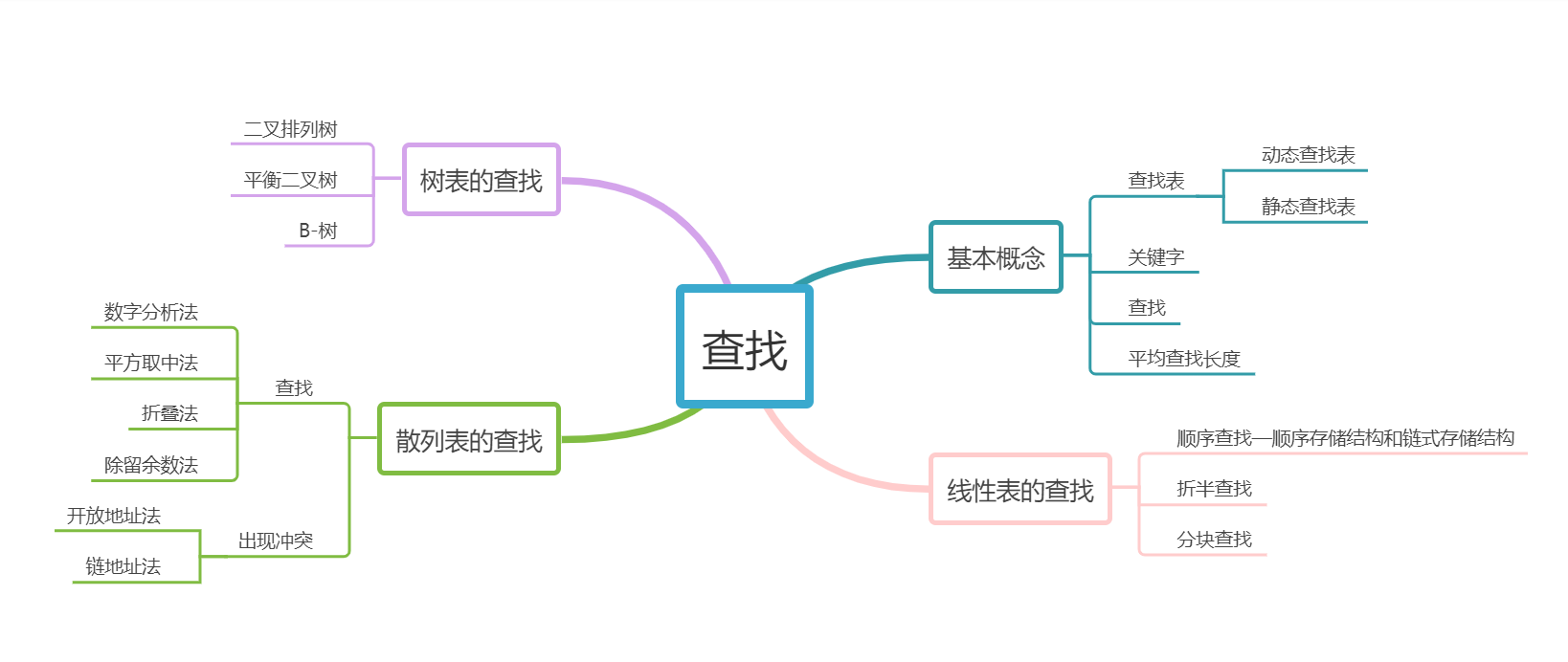
1、基本概念:
查找表(同一类型的数据元素或记录构成的集合);
关键字(数据元素或记录中的某个数据项的值,用它来标识一个数据元素或记录);
查找(在查找表中确定一个其关键字等于给定值的记录或数据元素,“查找成功”和“查找不成功”);
动态查找表和静态查找表(查找的同时对表进行修改操作,该表为动态查找表;只进行查找不进行修改,该表为静态查找表);
平均查找长度(ASL,在查找中,由于所耗费的时间在关键词的比较上,所以把平均需要和待查找值比较的关键词的次数称为平均查找长度)
2、线性表的查找:顺序查找、折半查找、分块查找(更适用于静态查找表)
顺序查找适用于线性表的顺序存储结构、链式存储结构

1 int Search_Seq(SSTable ST,KeyType key) 2 {//在顺序表 ST 中顺序查找其关键字等于 key 的数据元素。若找到,则函数值为该元素在表中的位置,否则为 0 3 ST.R[O] .key=key; //"哨兵” 4 for(i=ST.length;ST.R[i] .key!=key;--i); 5 return i; //从后往前找 6 }
折半查找(二分查找)要求只能是线性表的顺序储存结构

1 int Search_Bin(SSTable ST,KeyType key) 2 { //在有序表ST 中折半查找其关键字等于key的数据元素。若找到, 则函数值为该元素在表中的位置, 否则为0 3 low= 1;high=ST.length; //置查找区间初值 4 while(low<=high) 5 { 6 rnid=(low+high)/2; 7 if{key==ST.R[mid] .key) return mid; //找到待查元素 8 else if{key<ST.R[mid] .key) high=mid-1; //继续在前一子表进行查找 9 else low=mid+l; //继续在后一子表进行查找 10 } 11 return 0; //表中不存在待查元素 12 }
分块查找
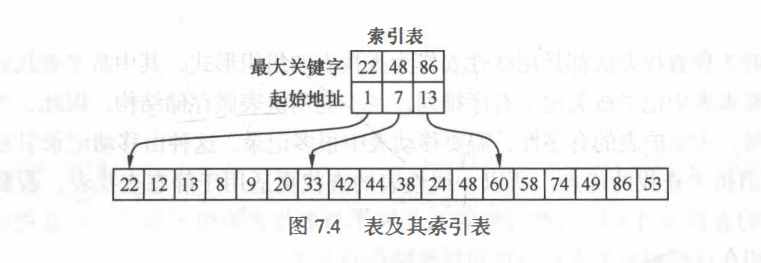
***
顺序查找:ASL=(n+1)/2 时间复杂度:O(n)
折半查找:ASL=log2(n + 1)-1 时间复杂度:O(log2 n)
3、树表的查找:二叉排序树、平衡二叉树、B-树
二叉排序树:中序遍历一棵二叉树可以得到一个结点值递增的有序序列(右>根>左)
二叉排序树查找算法的性能取决于二叉树的结构,而 二叉排序树的形状则取决于其数据集。如果数据呈有序排列,则二叉排序树是线性的,查找的时间复杂度为O(n); 反之,如果二叉排序树的结构合理,则查找速度较快,查找的时间复杂度为 O(log2 n)。

1 BSTree SearchBST (BSTree- T, KeyType key) _, 2 { //在根指针T所指二叉排序树中递归地查找某关键字等于key的数据元素,若查找成功 , 则返回指向该数据元素结点的指针, 否则返回空指针 3 if ((! T) || key==T->data. key) return T; //查找结束 4 else if (key<T->data. key) return SearchBST (T->lchild, key); //在左子树中继续查找 5 else return SearchBST (T->rchild, key) ; //在右子树中继续查找 6 }

1 void InsertBST(BSTree &T,ElemType e} 2 {//当二叉排序树 T中不存在关键字等千e.key的数据元素时, 则插入该元素 3 if (!T) //找到插入位置 , 递归结束 4 { 5 S=new BSTNode; //生成新结点*S 6 S->data=e; //新结点*S的数据域置为e 7 S->lchild=S->rchild=NULL; /新结点*S作为叶子结点 8 T=S; //把新结点*S链接到已找到的插入位置 9 else if (e. key<T->data. key) 10 InsertBST(T->lchild, e ); //将*S插入左子树 11 else if (e.key> T->da七a.key) 12 InsertBST(T->rchild, e); //将*S插入右子树 13 } 14 }
平衡二叉树:
平衡二叉树上所有结点的平衡因子只可能是-1、0和1;只要二叉树上有一个结点的平衡因子的绝对值大于1 则该二叉树就是不平衡的。
查找的时间复杂度是O(log2 n)。
查找的时间复杂度是O(log2 n)。
B-树:一种适用于外查找的平衡多叉树
4、散列表的查找(在元素的存储位置和其关键字之间建立某种直接关系)
(1)数字分析法 (2)平方取中法 (3)折叠法
(4)除留余数法:H(key)= key % p
出现冲突时:
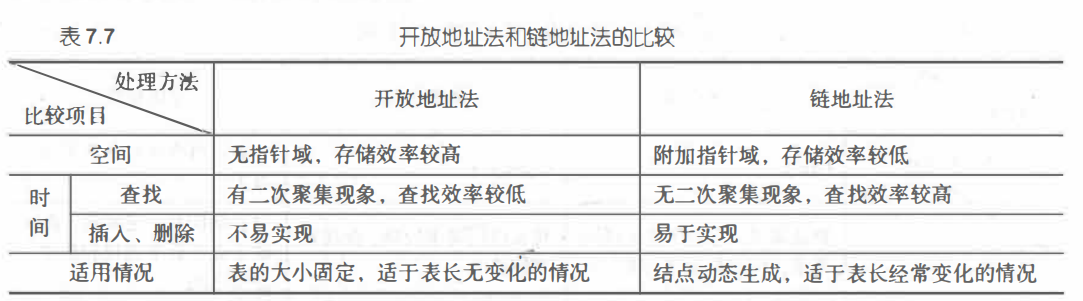
5、个人小结:
在前几章学的数据结构的基础上,这一章针对查找操作,分别的讨论了线性表、树表和散列表的查找算法效率。可能有前几章的铺垫加上端午几天假期,然后也是能够静下心来好好打代码。
主要还是想总结这一章的错题及原因:
(1)个人小测 “8-1 哈希表的构造与查找 ” 我居然把 10%11 算成了0(啊啊啊啊其实应该是10)
(2)实践:我的思路是 二分查找a【mid】=key的值,但是有个问题就是 有可能不存在跟key相等的a【mid】,那么就会退出循环(退出循环的条件是 low> high),去判断最后的a【low】,如果是小于key,则意味着 查找表中不存在,输出-1,如果是大于key,之间输出此时low的值(按照算法,在不断缩小的区间范围,是不断接近key的)




