[翻译]C#数据结构与算法 – 第六章BitArray类
BitArray类用于在资源有限的情况下表示一系列比特值。比特集合可以存储于常规数组,但是如果我们使用专为比特集合设计的数据结构则可以创建更高效的程序。在本章中,我们将学习一下怎样使用这种数据结构并研究一些可以使用比特集合来解决的问题。本章中同时复习了二进制数字,以及按位比较与移位运算符。
一个激起兴趣的问题
让我们看一个将最终使用BitArray类来解决的问题。这个问题的要求是找到质数。一个比较原始的方法是公元前三世纪的希腊哲学家埃拉托色尼发现的被称为爱拉托逊斯筛法的方法。这个方法过滤掉可以整除其它数字的数字,直到剩下的数字均为质数为止。例如,让我们找出前100个整数这个集合中的质数。我们由第一个质数2开始。我们遍历集合移除所有2的倍数。然后我们继续下一个质数3。我们再次遍历集合,移除所有3的倍数。接着我们移动到5,如此继续。当我们完成时,所有剩下的数字都是质数。
首先我们使用一个常规数组解决这个问题。我们将使用的这种方法与即将使用的用一个BitArray来解决问题的方法很类似,都是初始化数组的100个元素,并将每个元素的值置为1。由索引2开始(由于2是第一个质数),每个后来的数组索引都首先被查看值为1还是0。如果值为1,接着判断索引数是否为2的倍数。如果是,将这个索引位置的值设置为0。然后我们移动到索引3,进行相同的处理并继续。
要编写代码解决这个问题,我们将使用之前编写的Carray类。首先要做的是创建一个方法来执行筛选。如下是代码:
1 public void GenPrimes() 2 { 3 int temp; 4 for (int outer = 2; outer <= arr.GetUpperBound(0); outer++) 5 for (int inner = outer + 1; inner <= GetUpperBound(0); inner++) 6 if (arr[inner] == 1) 7 if ((inner % outer) == 0) 8 arr[inner] = 0; 9 }
现在我们仅需要就是一个显示质数的方法:
1 public void ShowPrimes() 2 { 3 for (int i = 2; i <= arr.GetUpperBound(0); i++) 4 if (arr[i] == 1) 5 Console.Write(i + " "); 6 }
下面是一个测试我们代码的程序:
1 static void Main() 2 { 3 int size = 100; 4 CArray primes = new CArray(size - 1); 5 for (int i = 0; i <= size - 1; i++) 6 primes.Insert(1); 7 primes.GenPrimes(); 8 primes.ShowPrimes(); 9 }
这个方法展示了怎样在整数数组中使用爱拉托逊斯筛法,但是更好的建议是使用比特来开发一个解决方案,因为这种数组中每个元素都是1或0。本章后面我们将学习怎样使用BitArray类来同时实现爱拉托逊斯筛法与其他将自己借位给比特集合的问题。
位与位操作
在我们研究BitArray类之前,我们需要研究怎样在VB.NET中使用位,由于在位一级操作是大多数VB.NET程序员所不熟悉的。在本节中,我们将学习怎样在VB.NET中操作位,主要通过学习怎样使用按位运算符操作比特值来学习。
二进制计数系统
在学习操作比特值之前,让我们复习一下二进制计数系统。二进制数字是使用0与1两个字符串来将基于10的(十进制)数字以基于2的数字来表示。例如,二进制中整数0表示如下:
00000000
整数1的二进制数字为:
00000001
如下是二进制中整数0-9所显示的形式:
00000000—0d (where d signifies a decimal number)
00000001—1d
00000010—2d
00000011—3d
00000100—4d
00000101—5d
00000110—6d
00000111—7d
00001000—8d
00001001—9d
最佳的将一个二进制数字转换为等值的十进制的方法是使用如下的方案。每一个二进制数字中,由最右端数字开始都代表了一个连续增大的2的幂。如果第一个位置上的数字是一个1,则其代表20。如果第二个位置有一个1,则其代表21,等等。
二进制数字:
00101010
等价于:
0 + 21 + 0 + 23 + 0 + 25 + 0 + 0 = 0 + 2 + 0 + 8 + 0 + 32 + 0 + 0 = 42
位通常显示于8个位的集合中,这组成了一个字节。使用8个位可以表示的最大数字为255,二进制如下:
11111111
或
1 + 2 + 4 + 8 + 16 + 32 + 64 + 128 = 255
一个大于255的数字必须存储于16位中。例如二进制数表示的256为:
00000001 00000000
虽然不是必须,但习惯上将低8位与高8位分隔。
操作二进制数字:按位操作与位移操作符
二进制数字并不使用基本算术运算符来操作。你必须使用按位操作运算符(And, Or, Not)或位移操作运算符(<<, >>, and >>>)。在这节中,我们解释这些运算符怎样工作并在后面的章节演示它们在VB.NET程序中的使用。
首先,我们研究按位操作运算符。这些大多数程序员已经熟悉的逻辑运算符 – 它们用来合并相关的表达式以便计算一个单一的布尔值。按位运算符操作二进制数字,逐位比较两个二进制数字,迭代生成一个新的二进制数字。
按位运算符以操作布尔值相同的方式工作。当操作二进制数字时,True位等价于1,False位等价于0。我们使用一个真值表来展示按位运算符对位的操作,正如对布尔值操作使用的真值表那样。一行中前两列为操作数,第三列为运算结果。And操作的真值表(布尔值表示)如下:
|
True |
True |
True |
|
True |
False |
False |
|
False |
True |
False |
|
False |
False |
False |
等价的位值的真值表:
|
1 |
1 |
1 |
|
1 |
0 |
0 |
|
0 |
1 |
0 |
|
0 |
0 |
0 |
Or操作的布尔值真值表为:
|
True |
True |
True |
|
True |
False |
True |
|
False |
True |
True |
|
False |
False |
False |
等价的位值的真值表:
|
1 |
1 |
1 |
|
1 |
0 |
1 |
|
0 |
1 |
1 |
|
0 |
0 |
0 |
最后是Xor运算符。这是最不被了解的一个按位运算符,因为其不用于计算机程序执行的逻辑运算。当两个位值进行Xor比较操作时,当两个位操作数中恰有一个为1时结果为1,如下是真值表:
|
1 |
1 |
0 |
|
1 |
0 |
1 |
|
0 |
1 |
1 |
|
0 |
0 |
0 |
将这些表格记在脑子中,我们使用这些操作符合并二进制数来迭代生成新的二进制数。如下是一些例子:
00000001 And 00000000 -> 00000000
00000001 And 00000001 -> 00000001
00000010 And 00000001 -> 00000000
00000000 Or 00000001 -> 00000001
00000001 Or 00000000 -> 00000001
00000010 Or 00000001 -> 00000011
00000000 Xor 00000001 -> 00000001
00000001 Xor 00000000 -> 00000001
00000001 Xor 00000001 -> 00000000
现在,让我们看一下一个VB.NET版的Windows应用程序更好的展示按位运算符的工作。
按位运算符应用程序
我们可以使用一个将这些运算符应用到一对值的Windows应用程序演示按位运算符的工作方式。我们将使用之前开发的ConvertBits方法帮助我们使用按位运算符。
首先,让我们看一下程序的用户界面,在解释程序的工作方式的过程中这界面将一直伴随着我们。
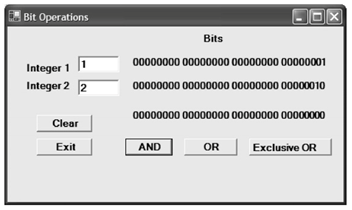
输入两个整数值,选择一种按位运算符的按钮。由每个整数值转换而来的位值与由按位运算符计算而得的位字符串结果一起显示出来。如下是一个例子,1与2这两个值进行AND运算的结果:
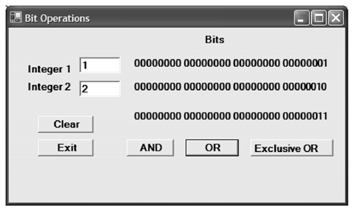
如下是1与2这两个值进行OR 运算的结果:
如下是操作的代码:
1 using System; 2 using System.Drawing; 3 using System.Collections; 4 using System.ComponentModel; 5 using System.Windows.Forms; 6 using System.Data; 7 using System.Text; 8 9 public class Form1 : System.Windows.Forms.Form 10 { 11 private System.Windows.Forms.Button btnAdd; 12 private System.Windows.Forms.Button btnClear; 13 private System.Windows.Forms.Button btnOr; 14 private System.Windows.Forms.Button btnXor; 15 private System.Forms.Label lblInt1Bits; 16 private System.Forms.Label lblInt2Bits; 17 private System.Forms.TextBox txtInt1; 18 private System.Forms.TextBox txtInt2; 19 20 // other Windows app code here 21 private void btnAdd_Click(object sender, System.EventArgs e) 22 { 23 int val1, val2; 24 val1 = Int32.Parse(txtInt1.Text); 25 val2 = Int32.Parse(txtInt2.Text); 26 lblInt1Bits.Text = ConvertBits(val1).ToString(); 27 lblInt2Bits.Text = ConvertBits(val2).ToString(); 28 } 29 30 private StringBuilder ConvertBits(int val) 31 { 32 int dispMask = 1 << 31; 33 StringBuilder bitBuffer = new StringBuilder(35); 34 for (int i = 1; i <= 32; i++) 35 { 36 if ((val && bitMask) == 0) 37 bitBuffer.Append("0"); 38 else 39 bitBuffer.Append("1"); 40 val <<= 1; 41 if ((i % 8) == 0) 42 bitBuffer.Append(" "); 43 } 44 return bitBuffer; 45 } 46 47 private void btnClear_Click(object sender, System.EventArgs e) 48 { 49 txtInt1.Text = ""; 50 txtInt2.Text = ""; 51 lblInt1Bits.Text = ""; 52 lblInt2Bits.Text = ""; 53 lblBitResult.Text = ""; 54 txtInt1.Focus(); 55 } 56 57 private void btnOr_Click(object sender, System.EventArgs e) 58 { 59 int val1, val2; 60 val1 = Int32.Parse(txtInt1.Text); 61 val2 = Int32.Parse(txtInt2.Text); 62 lblInt1Bits.Text = ConvertBits(val1).ToString(); 63 lblInt2Bits.Text = ConvertBits(val2).ToString(); 64 lblBitResult.Text = ConvertBits(val1 || val2).ToString(); 65 } 66 67 private void btnXOr_Click(object sender, System.EventArgs e) 68 { 69 int val1, val2; 70 val1 = Int32.Parse(txtInt1.Text); 71 val2 = Int32.Parse(txtInt2.Text); 72 lblInt1Bits.Text = ConvertBits(val1).ToString(); 73 lblInt2Bits.Text = ConvertBits(val2).ToString(); 74 lblBitResult.Text = ConvertBits(val1 ^ val2).ToString(); 75 } 76 }
移位操作符
一个二进制数字仅包含0与1,数字中每一位表示0或者一个2的幂值。C#中你可以使用3个运算符改变一个二进制数字中位的位置。它们是:左移运算符(<<)与右移运算符(>>)。
每个运算符都接受两个操作数:一个值(左侧操作数)与要将位移动的数目(右侧操作数)。例如,如果我们这样写:
1 << 1
结果是00000010。通过2 >> 1这个表达式我们又可以将结果逆回去。
看一个更复杂的例子。3的二进制数表示是:
00000011
如果进行3 << 1,结果是:
00000110
而如果进行3 << 2,结果是:
00001100
右移位运算符以与左移位运算符正好相反的方式工作。例如,如果编写3 >> 1
结果为00000001。
在本节的后面,我们将看到怎样编写一个Windows应用程序来展示移位运算符的使用。
整型到二进制转换程序
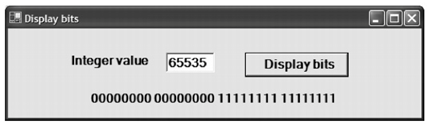
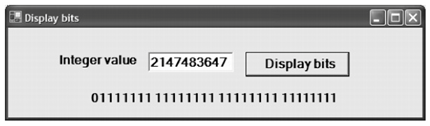
在本节中,我们展示了怎样使用一些位运算符来判断一个整数值中的位模式。用户输入一个整数值并按下Display bits按钮。整数值被转换为二进制后以8位一组的方式显示在一个label中。
我们用来将整数转换为二进制形式的核心工具是掩码。转换函数使用掩码来在显示一个数字中一些位时隐藏另一些位。当掩码与整数值(操作数)使用AND操作符合并时,结果是一个表示整数值二进制字符串。
首先,让我们看一些整数值及其二进制的表示:
计算机中负整数的二进制不总是那么易懂,正如这个例子中展示的。更多信息,参考一本有关汇编语言或计算机组织的书。
正如你看到的,这最后一个值,65535,是可以放入16位的最大数值。如果我们将数值增到65536,我们将得到下面的结果:
最后,让我们看一下将C#中可以存储的最大整数转换为二进制时会发生什么:
如果你尝试输入2147483648,你会看到一个错误。你可能会想最左边位的位置是可用的,但是实际上不可以的,因为那个位是用来处理负整数情况的。
现在让我们来看一下驱动这个程序的代码。我们将首先列出程序然后解释程序的工作方式:
1 using System; 2 using System.Drawing; 3 using System.Collections; 4 using System.ComponentModel; 5 using System.Windows.Forms; 6 using System.Data; 7 using System.Text; 8 9 public class Form1 : System.Windows.Forms.Form 10 { 11 // Windows generated code omitted here 12 private void btnOr_Click(object sender, System.EventsArgs e) 13 { 14 int val1, val2; 15 val1 = Int32.Parse(txtInt1.Text); 16 val2 = Int32.Parse(txtInt2.Text); 17 lblInt1Bits.Text = ConvertBits(val1).ToString(); 18 lblInt2Bits.Text = ConvertBits(val2).ToString(); 19 lblBitResult.Text = ConvertBits(val1 || val2).ToString(); 20 } 21 22 private StringBuilder ConvertBits(int val) 23 { 24 int dispMask = 1 << 31; 25 StringBuilder bitBuffer = new StringBuilder(35); 26 for (int i = 1; i <= 32; i++) 27 { 28 if ((val && bitMask) == 0) 29 bitBuffer.Append("0"); 30 else 31 bitBuffer.Append("1"); 32 val <<= 1; 33 if ((i % 8) == 0) 34 bitBuffer.Append(" "); 35 } 36 return bitBuffer; 37 } 38 }
这个程序中大部分工作由ConvertBits函数来完成。dispMask这个变量存储位掩码,bitBuffer这个变量存储函数构建的位字符串。bitBuffer被声明为一个StringBuilder类型的变量,以方便我们使用它的Append方法来构建字符串而不是用连接。
for循环中构建了二进制的字符串,其进行了32此迭代,正是由于我们构建一个32位的字符串。要构建位字符串,我们将值与位掩码进行AND运算。如果运算的结果是0,一个0被添加到字符串。如果结果是1,一个1被添加到字符串。然后我们在这个值上执行一次左移位以便接下来计算字符串中下一位。最后,没8位,我们向字符串添加一个空格以便分隔字符串为4个8位的子字符串,这样结果更易读。
位移动演示程序
本节讨论一个演示位移动运算符工作方式的Windows应用程序。这个程序提供两个文本框用来输入两个操作数(一个要进行移位的值与要移动的位数),两个label来显示左侧操作数与移位操作结果的位的原始的二进制表示。这个有两个按钮表示执行左移位还是右移位,以及一个清除按钮和一个退出按钮。
如下是程序的代码:
1 using System; 2 using System.Drawing; 3 using System.Collections; 4 using System.ComponentModel; 5 using System.Windows.Forms; 6 using System.Data; 7 using System.Text; 8 9 public class Form1 : System.Windows.Forms.Form 10 { 11 // Windows generated code omitted 12 private StringBuilder ConvertBits(int val) 13 { 14 int dispMask = 1 << 31; 15 StringBuilder bitBuffer = new StringBuilder(35); 16 17 for (int i = 1; i <= 32; i++) 18 { 19 if ((val && bitMask) == 0) 20 bitBuffer.Append("0"); 21 else 22 bitBuffer.Append("1"); 23 24 val <<= 1; 25 if ((i % 8) == 0) 26 bitBuffer.Append(" "); 27 } 28 return bitBuffer; 29 } 30 31 private void btnOr_Click(object sender, System.EventsArgs e) 32 { 33 txtInt1.Text = ""; 34 txtBitShift.Text = ""; 35 lblInt1Bits.Text = ""; 36 lblOrigBits.Text = ""; 37 txtInt1.Focus(); 38 } 39 40 private void btnLeft_Click(object sender, System.EventsArgs e) 41 { 42 int value = Int32.Parse(txtInt1.Text); 43 lblOrigBits.Text = ConvertBits(value).ToString(); 44 value <<= Int32.Parse(txtBitShift.Text); 45 lblInt1Bits.Text = ConvertBits(value).ToString(); 46 } 47 48 private void btnRight_Click(object sender, System.EventsArgs e) 49 { 50 int value = Int32.Parse(txtInt1.Text); 51 lblOrigBits.Text = ConvertBits(value).ToString(); 52 value >>= Int32.Parse(txtBitShift.Text); 53 lblInt1Bits.Text = ConvertBits(value).ToString(); 54 } 55 }
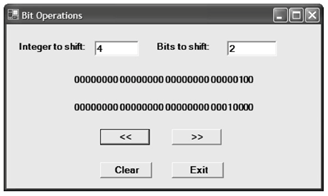
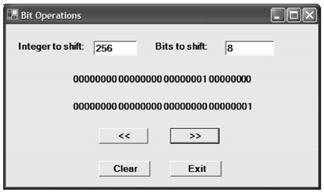
下面是运行中程序的一些例子。
如下是4<<2:
如下是256 >> 8:
BitArray类
BitArray类用于与位集合一起工作。一个位集合用于高效的表示一系列的布尔值。BitArray与ArrayList非常类似,如当添加位会超过数组的上界时无需担心,因为BitArray大小可以被动态的调整。
使用BitArray类
向构造函数中传入你想要的比特位的数目这样可以初始化一个BitArray对象:
1 BitArray BitSet = new BitArray(32);
这个BitArray对象的32个位均被设置为False。如果我们想让它们为True,我们可以这样初始化位数组:
1 BitArray BitSet = new BitArray(32, true);
这个类的构造函数有许多不同形式的重载,但是这里我们将仅仅再看另外一种构造函数。你可以使用一个字节(Byte)数组来初始化一个BitArray。例如:
1 byte[] ByteSet = new byte[] { 1, 2, 3, 4, 5 }; 2 BitArray BitSet = new BitArray(ByteSet);
这个比特集合 – BitArray目前包含了字节值1,2,3,4和5的位。
位存储于BitArray时,最重要的位放在最左侧(索引0处)的位置。当你阅读二进制数字的习惯是自右向左时这可能会引起阅读的混乱。例如,如下是一个与数字1等值的一个8位BitArray的内容:
True False False False False False False False
当然,我们更习惯查看一个最主要位在右侧二进制数字,如:
0 0 0 0 0 0 0 1
我们将不得不编写我们自己的代码来更改显示方式为位值(而不是布尔值)与位值常用的显式顺序。
如果BitArray中有字节值,每个字节值的每个位在遍历数组时将显示。如下是一个简单的遍历一个字节值的BitArray的程序片段:
1 byte[] ByteSet = new byte[] { 1, 2, 3, 4, 5 }; 2 BitArray bitSet = new BitArray(ByteSet); 3 for (int bits = 0; bits <= bitSet.Count - 1; bits++) 4 Console.Write(bitSet.Get(bits) + " ");
如下是输出:
这种输出几 乎不可读,它几乎没法真实的反应数组中存储的内容。稍后我们将看到怎样使这类BitArray变得简单易理解。首先,我们需要了解怎样由一个BitArray中检索位值。
BitArray中存储的单独的位使用Get方法来检索。这个方法接受一个整型的参数 - 即希望检索的值的索引,并返回true或false表示的位置。Get方法用于代码段的前部来显示BitArray中的位值。
如果我们存储于BitArray的数据实际上是二进制值(那样,值应该被表示为0与1),我们需要以恰当的顺序 - 由右侧开始而不是左侧来使用0与1这种方式显示值。虽然我们不能改变BitArray类使用的内部代码,我们可以编写外部代码得到想要的输出。
如下程序创建了一个有5个字节值(1,2,3,4,5)的BitArray,并以恰当的二进制格式显示每个字节:
1 using System; 2 using System.Collections; 3 4 class chapter6 5 { 6 static void Main() 7 { 8 int bits; 9 string[] binNumber = new string[8]; 10 int binary; 11 byte[] ByteSet = new byte[] { 1, 2, 3, 4, 5 }; 12 BitArray BitSet = new BitArray(ByteSet); 13 bits = 0; 14 binary = 7; 15 for (int i = 0; i <= BitSet.Count - 1; i++) 16 { 17 if (BitSet.Get(i) == true) 18 binNumber[binary] = "1"; 19 else 20 binNumber[binary] = "0"; 21 bits++; binary--; 22 if ((bits % 8) == 0) 23 { 24 binary = 7; 25 bits = 0; 26 for (int j = 0; j <= 7; j++) 27 Console.Write(binNumber[j]); 28 } 29 } 30 } 31 }
如下是输出:
00000001
00000010
00000100
00000101
这个程序中使用了两个数组。第一个数组,BitSet,是一个BitArray,存储字节值(位格式)。第二个数组,binNumber,只是一个字符串数组用于存储一个二进制字符串。这个二进制字符串将由每一个比特值的位构建,由最后一个位置(7)开始向前移动至第一个位置(0)。
每次当一个位值被处理的时候,其首先转换为1(如果是true)或0(如果为false),然后被放置于适当的位置。两个变量指示我们的处理过程在BitSet数组(位)与binNumber数组(二进制)的位置。我们也需要知道当我们将8个位转换后结果是一个数字。我们通过将当前位值(在位变量中)对8去模来完成这个工作。如果当前不再有剩余则我们到了第8个位并得到一个数字的结果,否则将继续这个循环。
我们将这个程序完全实现于Main()函数中,但是在本章最后的联系中你将有机会通过创建一个类甚至是扩展BitArray类包含这个转换技术来完善这个程序。
更多BitArray类方法与属性
在本节,我们讨论另外一些使用BitArray类时你最有可能用到的方法与属性。
Set方法将用于给一个特定的位指定一个值。这个方法使用方式如下:
BitArray.Set(bit, value)
要设置的位通过索引(第一个参数)来指定,第二个参数value(布尔类型)是你希望给这个位指定的布尔值。(虽然布尔值是应该在这里考虑使用的,事实上你也可以使用其它值,如0与1。在下一节你将看到怎样实现这个功能)
SetAll方法允许你将所有的位值设置为一个你通过参数传入的值,如BitSet.SetAll(false)。
你可以在一对BitArray对象的所有位上使用And,Or,Xor与Not方法完成逐位操作。例如,我们有两个BitArray,bitSet1与bitSet2,我们可以按如下方式执行一个按位Or操作:
1 bitSet1.Or(bitSet2);
如下表达式:
1 bitSet.Clone();
返回一个BitArray的浅拷贝,而如下表达式:
1 bitSet.CopyTo(arrBits);
将BitArray的内容拷贝到一个名为arrBits的普通数组。
结束这些概览后,现在我们可以开始了解怎样使用一个BitArray来编写爱拉托逊斯筛法。
使用BitArray完成爱拉托逊斯筛法
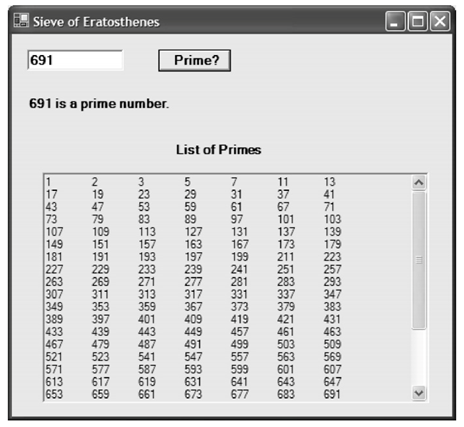
在本章开始处,我们展示了怎样使用一个基本数组编写程序来实现爱拉托逊斯筛法。在本节,我们展示了相同的算法,这次使用BitArray来实现这个查找素数的方法。
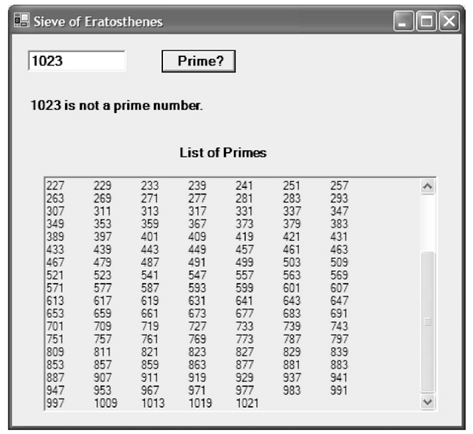
我们编写的这个程序接受用户输入的整数值,并判断这个数是否为素数,同时展示了一个由1到1024中所有的素数的列表。下面是这个程序的部分截图:
当这个数字不是素数时将会有如下结果:
下面让我们看一下代码:
1 using System; 2 using System.Drawing; 3 using System.Collections; 4 using System.ComponentModel; 5 using System.Windows.Forms; 6 using System.Data; 7 using System.Text; 8 9 public class Form1 : System.Windows.Forms.Form 10 { 11 // Windows generated code omitted 12 private void btnPrime_Click(object sender, System.EventsArgs e) 13 { 14 BitArray bitSet = new BitArray(1024); 15 int value = Int32.Parse(txtValue.Text); 16 BuildSieve(bitSet); 17 if (bitSet.Get(value)) 18 lblPrime.Text = (value + " is a prime number."); 19 else 20 lblPrime.Text = (value + " is not a prime number."); 21 } 22 23 private void BuildSieve(BitArray bits) 24 { 25 string primes; 26 for (int i = 0; i <= bits.Count - 1; i++) 27 bits.Set(i, true); 28 29 int lastBit = Int32.Parse(Math.Sqrt(bits.Count).ToString()); 30 for (int i = 2; i <= lastBit - 1; i++) 31 if (bits.Get(i)) 32 for (int j = 2 * i; j <= bits.Count - 1; j++) 33 bits.Set(j, false); 34 35 int counter = 0; 36 for (int i = 1; i <= bits.Count - 1; i++) 37 if (bits.Get(i)) 38 { 39 primes += i.ToString(); 40 counter++; 41 if ((counter % 7) == 0) 42 primes += "\n"; 43 else 44 primes += "\n"; 45 } 46 txtPrimes.Text = primes; 47 } 48 }
如下这个循环中分配了筛子:
1 int lastBit = Int32.Parse(Math.Sqrt(bits.Count).ToString()); 2 for (int i = 2; i <= lastBit - 1; i++) 3 if (bits.Get(i)) 4 for (int j = 2 * i; j <= bits.Count - 1; j++) 5 bits.Set(j, false);
这个循环遍历了从开始一直到BitArray项的数目的平方根那个数的倍数,这个过程中去掉2,3,4,5等数字的倍数。
一旦数组使用筛子构建完毕,我们可以执行一个对BitArray的简单调用:
1 bitSet.Get(value)
如果这个值可以找到,这个值就是一个素数。如果找不到,则它已经被筛子过滤掉,这个数不是素数。
使用BitArray与Array实现的比较
使用BitArray类处理有布尔值或比特值参与的问题被认为是更高效的。一些看起来不涉及这样类型值的问题可以被重新设计以便BitArray可以派上用场。
如果对一个使用BitArray与一个使用基本数组完成的爱拉托逊斯筛法进行计时,使用BitArray的方法一般要快2倍。在练习中你将有机会亲身查看这些结果。
摘要
BitArray类用于存储位的集合。虽然比特通常用0与1表示,但是BitArray类存储True或False来取而代之。当你需要存储一系列的布尔值BitArray就很有用,但是当你需要操作比特时BitArray更有用,因为你可以在比特值与布尔值之间轻松的转换。
正如本章与其中之一联系所展示的那样,可以使用数字数组解决的问题可以使用比特数组更有效的解决。虽然一些读者可能只将这当成一种新奇(或者已经不再感觉新奇)的编程技巧,但一些特定场景下这种高效存储比特值或布尔值的方法是不能被拒绝的。
练习
1. 编写你自己的BitArray类(不要继承自BitArray类),其中包括一个可以接受布尔值并将其转换为比特值的方法。提示:使用BitArray类作为你编写的类的主要的数据结构,然后添加你实现的其它方法。
2. 重新实现题目1所要求的问题,但这次你的类需继承自BitArray,然后你再添加自己的方法。
3. 使用题目1或2中设计的任意一个BitArray类,编写一个方法取得一个整数值,将其比特值反转,并将新值以10进制显示。
4. 在编程珠玑这本经典编程著作中,作者Jon Bentley讨论了有关使用BitArray的编程问题的解决方案,虽然书中称BitArray为比特向量。在下面的网站阅读这个问题:
http://www.cs.bell-labs.com/cm/cs/pearls/cto.html
使用VB.NET设计你的解决方案,最小化这个问题所用的数据存储。当然你不需要使用书中所用的那么大的文件,找一些足够测试你的实现的东西就好。
5. 编写一个程序比较使用BitArray与使用基本数组实现爱拉托逊斯筛法的耗时。你的结果如何?









【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 从 HTTP 原因短语缺失研究 HTTP/2 和 HTTP/3 的设计差异
· AI与.NET技术实操系列:向量存储与相似性搜索在 .NET 中的实现
· 基于Microsoft.Extensions.AI核心库实现RAG应用
· Linux系列:如何用heaptrack跟踪.NET程序的非托管内存泄露
· 开发者必知的日志记录最佳实践
· TypeScript + Deepseek 打造卜卦网站:技术与玄学的结合
· Manus的开源复刻OpenManus初探
· AI 智能体引爆开源社区「GitHub 热点速览」
· C#/.NET/.NET Core技术前沿周刊 | 第 29 期(2025年3.1-3.9)
· 从HTTP原因短语缺失研究HTTP/2和HTTP/3的设计差异