01.linear regression note

01.note

正文链接：https://jovian.ai/aakashns/02-linear-regression

一.不用pytorch的module模型手写简单的线性问题

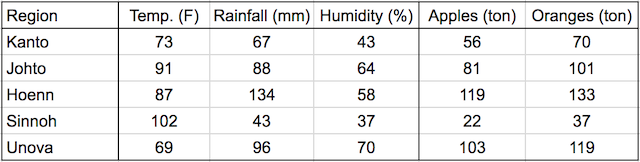
1）输入train_data和test_data

#1.输入数据集
inputs = np.array([[73, 67, 43],
                   [91, 88, 64],
                   [87, 134, 58],
                   [102, 43, 37],
                   [69, 96, 70]], dtype='float32')

targets = np.array([[56, 70],
                    [81, 101],
                    [119, 133],
                    [22, 37],
                    [103, 119]], dtype='float32')
inputs = torch.from_numpy(inputs)
targets = torch.from_numpy(targets)

2）确定W和b的形状 初始化W和b

首先明确函数，该问题有两条函数：

注意：W的上标表示该W为第几条函数的W

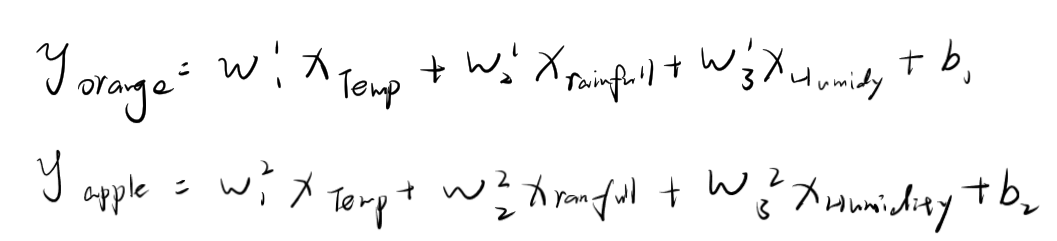
确定形状：

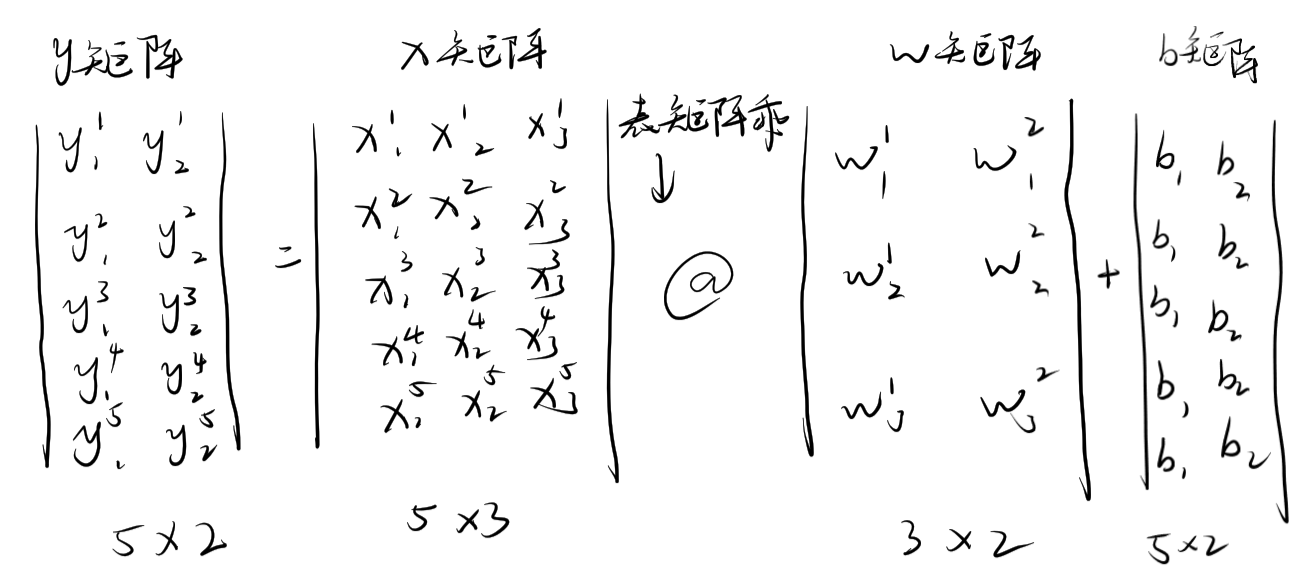
矩阵和公式契合。

值得注意的是：在pytorch中，计算y(hat)的值并非是 y = wx+b 而是 y = x*w.t()+b，所以这里W的形状不是3,2，而是2,3，且w,b需要计算梯度

code：

w = torch.randn(2, 3, requires_grad=True)
b = torch.randn(2, requires_grad=True)

3).定义前馈函数

def module(x):
    return x@w.t()+b

4)定义Loss函数，采用均方差

def mse(t1, t2):
    diff = t1 - t2
    return torch.sum(diff * diff) / diff.numel()#numel返回torch对象里的元素个数，这里是10 target大小一致

5）train

for i in range(10000):
    preds = model(inputs)
    loss = mse(preds, targets)
    #pytorch框架自动计算loss中的梯度，并存储在w,b中
    loss.backward() 
    print(loss)

    with torch.no_grad():
        w -= w.grad * 1e-5
        b -= b.grad * 1e-5
        w.grad.zero_()
        b.grad.zero_()

里面值得注意的是：

 with torch.no_grad():

当我们不想进行梯度的计算时，加上这一行代码

loss变换结果：

tensor(26934.1621, grad_fn=<DivBackward0>)
tensor(18410.7305, grad_fn=<DivBackward0>)
tensor(12663.6895, grad_fn=<DivBackward0>)

.....

tensor(0.5032, grad_fn=<DivBackward0>)
tensor(0.5032, grad_fn=<DivBackward0>)
tensor(0.5032, grad_fn=<DivBackward0>)

全部代码：

import numpy as np
import torch

#1.输入数据集
inputs = np.array([[73, 67, 43],
                   [91, 88, 64],
                   [87, 134, 58],
                   [102, 43, 37],
                   [69, 96, 70]], dtype='float32')

targets = np.array([[56, 70],
                    [81, 101],
                    [119, 133],
                    [22, 37],
                    [103, 119]], dtype='float32')
inputs = torch.from_numpy(inputs)
targets = torch.from_numpy(targets)

#2.确定w,b矩阵
w = torch.randn(2, 3, requires_grad=True)
b = torch.randn(2, requires_grad=True)

#3.定义前馈函数
def model(x):
    return x@w.t() + b

#4.定义Loss function，MSE(均方差) numel()返回torch对象中元素的个数
def mse(t1, t2):
    diff = t1 - t2
    return torch.sum(diff * diff) / diff.numel()

for i in range(10000):
    preds = model(inputs)
    loss = mse(preds, targets)
    loss.backward()
    print(loss)

    with torch.no_grad():
        w -= w.grad * 1e-5
        b -= b.grad * 1e-5
        w.grad.zero_()
        b.grad.zero_()

二.引入pytorch框架的model与Dataset and DataLoader简化上述过程

import

import numpy as np
import torch
from torch.utils.data import TensorDataset
from torch.utils.data import DataLoader
import torch.nn as nn #构建model
import torch.nn.functional as F #构建loss function

1.数据划分

#1.数据划分
train_ds = TensorDataset(inputs,targets)
batch_size = 5
train_dl = DataLoader(train_ds, batch_size, shuffle=True) 

TensorDataset和DataLoader一般一起使用,用于将数据分块,batch_size是每块所含有的行数,shuffle参数是将数据打乱。

for xb, yb in train_dl:
    print(xb)
    print(yb)
    break
#结果是
tensor([[102.,  43.,  37.],
        [ 92.,  87.,  64.],
        [ 87., 134.,  58.],
        [ 69.,  96.,  70.],
        [101.,  44.,  37.]])
tensor([[ 22.,  37.],
        [ 82., 100.],
        [119., 133.],
        [103., 119.],
        [ 21.,  38.]])

若想从train_ds,或train_dl中各自取得trainset和testset，可以采取下面的方式，支持切片

x,y = train_ds[:,:]
print("x:",x)
print("y:",y)

#结果是：
x: tensor([[ 73.,  67.,  43.],
        [ 91.,  88.,  64.],
        [ 87., 134.,  58.],
        [102.,  43.,  37.],
        [ 69.,  96.,  70.]])
y: tensor([[ 56.,  70.],
        [ 81., 101.],
        [119., 133.],
        [ 22.,  37.],
        [103., 119.]])

2.使用model构建w b

#2.构建model
model = nn.Linear(3, 2)#传入w的形状后，其实bias的形状也就确定了，这里也是随机构成
print(model.weight)
print(model.bias)
#结果
tensor([[ 0.5272,  0.1223, -0.1660],
        [ 0.5324, -0.2326, -0.0065]], requires_grad=True)
Parameter containing:
tensor([-0.1113,  0.2527], requires_grad=True)

3.构建loss function

#3.构建loss function
loss_fn = F.mse_loss

当需要计算loss的时候，只需要传入input前馈后的值和标准值target, 该函数会自己用mse去计算loss.并将w的梯度计算存储在计算图内。

loss = loss_fn(model(inputs), targets)

4.构建optimizer(用于改变w,b的值),并设定学习率

opt = torch.optim.SGD(model.parameters(), lr=1e-5)

model.parameters()里面就是w与b。lr为学习率, w(new) = w(old) - lr*gradient.

5.训练

#5.训练
num_epochs=10000
for epoch in range(num_epochs):
    #x,y为train和target数据,每个数据块为5行
    for x,y in train_dl:
        #1.前馈
        pre = model(x)
        #2.计算loss
        loss = loss_fn(pre,y)
        print(loss)
        #3.计算梯度
        loss.backward()
        #4.优化w,b
        opt.step()
        #5.重置梯度
        opt.zero_grad()

loss变化为：

tensor(15312.8965, grad_fn=<MseLossBackward>)
tensor(10408.4082, grad_fn=<MseLossBackward>)
tensor(7102.2720, grad_fn=<MseLossBackward>)

。。。。

tensor(0.5017, grad_fn=<MseLossBackward>)
tensor(0.5017, grad_fn=<MseLossBackward>)
tensor(0.5017, grad_fn=<MseLossBackward>)

整体代码：

import numpy as np
import torch
from torch.utils.data import TensorDataset
from torch.utils.data import DataLoader
import torch.nn as nn
import torch.nn.functional as F
#1.预处理数据
inputs = np.array([[73, 67, 43],
                   [91, 88, 64],
                   [87, 134, 58],
                   [102, 43, 37],
                   [69, 96, 70]], dtype='float32')

targets = np.array([[56, 70],
                    [81, 101],
                    [119, 133],
                    [22, 37],
                    [103, 119]], dtype='float32')
inputs = torch.from_numpy(inputs)
targets = torch.from_numpy(targets)

train_ds = TensorDataset(inputs,targets)
batch_size = 5
train_dl = DataLoader(train_ds, batch_size, shuffle=True)

#2.构建model
model = nn.Linear(3, 2)
print(model.weight)
print(model.bias)

#3.构建loss function
loss_fn = F.mse_loss

#4.构建opimizer
opt = torch.optim.SGD(model.parameters(), lr=1e-5)

#5.训练
num_epochs=10000
for epoch in range(num_epochs):
    #x,y为train和target数据,每个数据块为5行
    for x,y in train_dl:
        #1.前馈
        pre = model(x)
        #2.计算loss
        loss = loss_fn(pre,y)
        print(loss)
        #3.计算梯度
        loss.backward()
        #4.优化w,b
        opt.step()
        #5.重置梯度
        opt.zero_grad()