字典树及其应用
9.trie字典树
835.trie字符串统计
维护一个字符串集合,支持两种操作:
- “I x”向集合中插入一个字符串x;
- “Q x”询问一个字符串在集合中出现了多少次。
共有N个操作,输入的字符串总长度不超过 105105,字符串仅包含小写英文字母。
输入格式
第一行包含整数N,表示操作数。
接下来N行,每行包含一个操作指令,指令为”I x”或”Q x”中的一种。
输出格式
对于每个询问指令”Q x”,都要输出一个整数作为结果,表示x在集合中出现的次数。
每个结果占一行。
数据范围
1≤N≤2∗1041≤N≤2∗104
输入样例:
5
I abc
Q abc
Q ab
I ab
Q ab
输出样例:
1
0
1
代码以及思路:
#include<iostream>
#include<string>
using namespace std;
//son数组里面存放了它是第几个节点,cnt存放了以该节点结束的字符串个数。
//举例1):存放 "ab" "cb"
//1 0 3 0
// 2
// 4
//举例2):存放 "ab" "ac"
//1 0 0 0
// 2 3
//
//其实可以看到,有一个很巧妙的点,一个数的子节点的行数正好是它的父节点的index值,如 3的子节点就是4,而4则在第3行
//插入所有字符串的字符总和不会超过10e5
const int N = 10e5 + 10;
//保存节点,里面每个元素是插入节点的序号
int son[N][26];
//储存了以第i个插入字母结尾的字符串个数
int cnt[N];
//插入元素序号 始终等于最后一个插入元素的序号
int idx = 0;
void insert(const string &s) {
int next = 0;
for (int i = 0; i < s.size(); i++) {
//bias为列
int bias =s[i] -'a';
if (son[next][bias] == 0) son[next][bias] = ++idx;
next = son[next][bias];
}
//出循环之后,next里存储的就是该字符串最后一个字符对应的idx;注意不能使用idx,因为可能插入 ab,c,ab。在最后一个b插入的时候,idx指向的是c。
cnt[next]++;
}
int querry(const string &s) {
int next = 0;
for (int i = 0; i < s.size(); i++) {
int bias = s[i] - 'a';
if (son[next][bias] == 0) return 0;
//若不为0,则跳去它的子节点
next = son[next][bias];
}
//最终,next的值就为最后一个字符所对应的Idx值
return cnt[next];
}
int main() {
int m;
cin >> m;
while (m--) {
char op;
string s;
cin >> op;
cin >> s;
if (op == 'I') insert(s);
else if (op == 'Q') cout << querry(s) << endl;
}
}
143.最大异或树
在给定的N个整数A1,A2……ANA1,A2……AN中选出两个进行xor(异或)运算,得到的结果最大是多少?
输入格式
第一行输入一个整数N。
第二行输入N个整数A1A1~ANAN。
输出格式
输出一个整数表示答案。
数据范围
1≤N≤1051≤N≤105,
0≤Ai<2310≤Ai<231
输入样例:
3
1 2 3
输出样例:
3
代码及其思路:
当计算异或时,同一位数据相反则取1。若使用朴素做法,时间复杂度位O(n^2);
这里采取字典树进行优化。将所有的数据装入字典树:
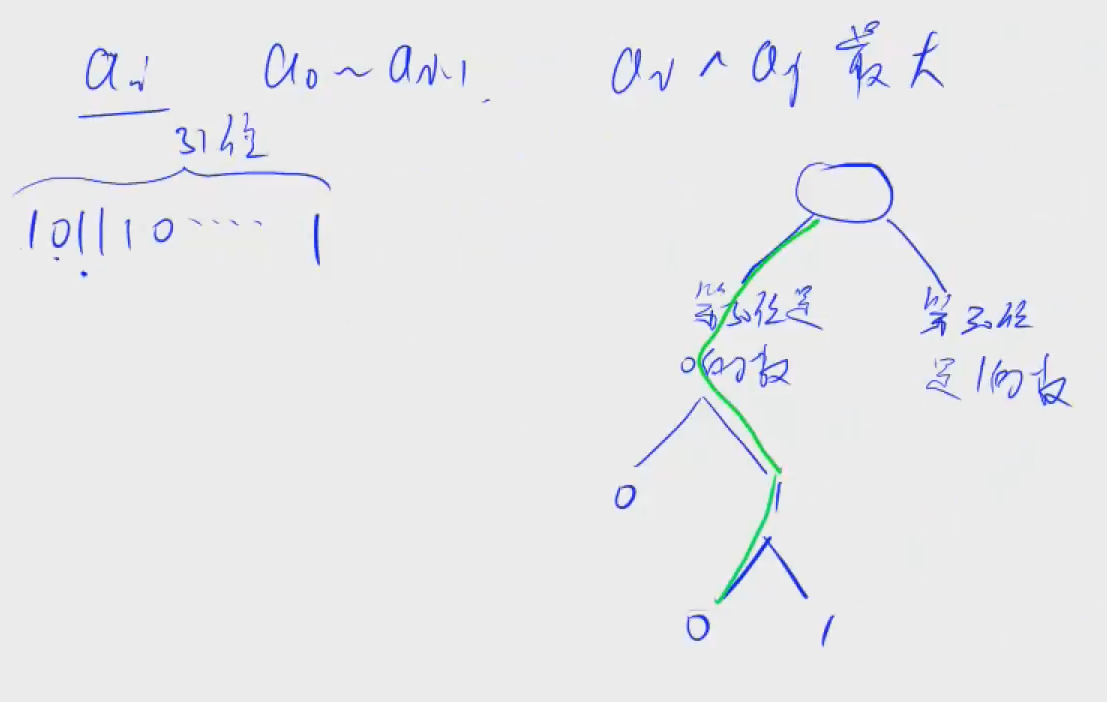
所有数据都为32位,依旧是两层循环,不过简化了第二层循环。a[i]的每一位和字典树的每一层进行匹配,如 1101,若字典树有开头为0的,则走0,因为1101的第一位是0。匹配到第三位的时候,若在第三层有1则走1,因为1101的第三层位0。数据相反异或为1,否则为0。从头开始贪心进行匹配,因为高位是1更管用。
#include<iostream>
#include<algorithm>
using namespace std;
//整体思路和trie树一样,将所有的数据插入树中,构成搜索树,再按位进行选择
const int N = 10e5 + 10;
int a[N];//保存输入数据
int son[31*N][2], idx;
void insert(int x) {
//next保存子节点的行数
int next = 0;
for (int i = 30; i >= 0; i--) {
//获得待插入位数上的值
int bias = x >> i & 1;
if (son[next][bias] == 0) son[next][bias] = ++idx;
next = son[next][bias];
}
}
int querry(int x) {
int next = 0;
int res = 0;
for (int i = 30; i >= 0; i--) {
int bias = x >> i & 1;
//若没有相反值 则将就走下同值
if (son[next][!bias] == 0) {
next = son[next][bias];
res = res * 2 + bias;
}
else {
//有相反值走相反值
next = son[next][!bias];
res = res * 2 + !bias;
}
}
return res;
}
int main() {
int m;
cin >> m;
for (int i = 0; i < m; i++) {
cin >> a[i];
insert(a[i]);
}
int res = 0;
for (int i = 0; i < m; i++) {
int q = querry(a[i]);
res = max(res, a[i]^q);
}
cout << res;
return 0;
}


