归并排序以及逆序对问题

归并排序以及逆序对问题

void merge_sort(int q[], int l, int r)
{
    if(l >= r) return;
    

    int mid = l+r>>1;
    merge_sort(q,l,mid);
    merge_sort(q,mid+1,r);
    
    int tmp[r-l+1]={0}, k = 0, i = l, j = mid+1;
    while(i<=mid && j<=r){
        if(q[i]<=q[j]) tmp[k++] = q[i++];
        else tmp[k++] = q[j++];
    }
    
    while(i<=mid) tmp[k++] = q[i++];
    while(j<=r) tmp[k++] = q[j++];
    
    for(int i = l, j = 0; i<=r; i++,j++) q[i] = tmp[j];
}

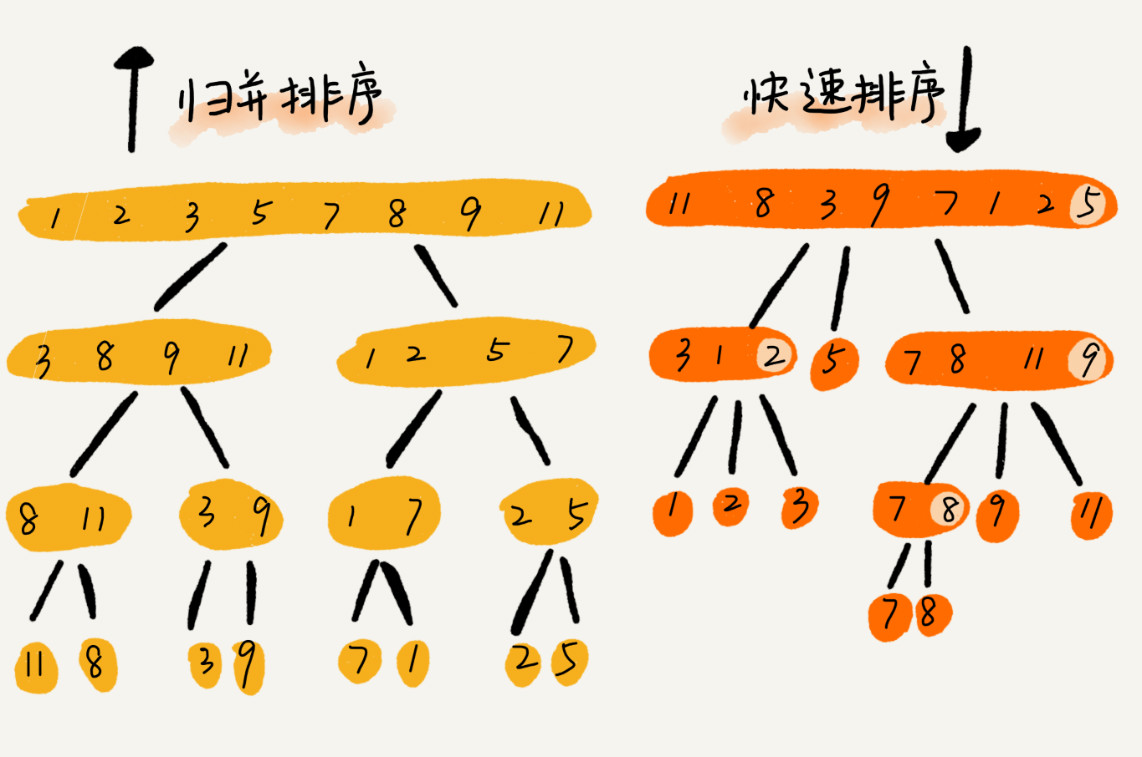
归并排序与快速排序的分治合差别：

归并是从下往上进行出递归的时候进行数据的处理，要进行合并。

快速排序是从上往下的时候进行分治，不用进行合并。

习题：

788.逆序对的数量

给定一个长度为n的整数数列，请你计算数列中的逆序对的数量。

逆序对的定义如下：对于数列的第 i 个和第 j 个元素，如果满足 i < j 且 a[i] > a[j]，则其为一个逆序对；否则不是。

输入格式

第一行包含整数n，表示数列的长度。

第二行包含 n 个整数，表示整个数列。

输出格式

输出一个整数，表示逆序对的个数。

int res;
void merge_sort(int q[], int l, int r){
    if(l >= r) return;
    

    int mid = l + r >> 1;
    merge_sort(q, l ,mid);
    merge_sort(q, mid+1, r);
    
    int tmp[r-l+1] = {0}, k = 0 ,i = l, j = mid+1; 
    while(i <= mid&& j<=r){
        if(q[i] <= q[j]) tmp[k++] = q[i++];
        else{
            tmp[k++] = q[j++];
            //重点
            res+=mid-i+1;
        }
    }

    while(i <= mid) tmp[k++] = q[i++];
      
    
    while(j <= r) tmp[k++] = q[j++];
    
    for(int i = l, j = 0; i <= r; i++,j++) q[i] = tmp[j];

}

为什么只在归并排序的基础上增加了：

res+=mid-i+1;

就能解出这道题？

假设在最后一次排列中的数据为

2 3 4 || 1 5 6

mid = 4 ; i =2; j = 5;

首先，两部分数据在上一层递归中已经得到了排序，所以两部分数据均为有序状态。因此，上一层递归的逆序对已经算出。我们只需要将res加上本层递归所算出来的逆序对个数即可。

可以很明显的看出，要先放置1在temp中，放了1之后，从i~mid都会比1大，因为程序中经过了此次对比

if(q[i] > q[j]) tmp[k++] = q[j++];

在左右两边均为有序的状态下，左边会有i - mid+1个数比此时的q[j]大，所以要用 res+=i-mid+1.