快速排序以及快速选择问题

1.快速排序

模板

1）单向划分

void quick_sort(int q[], int l, int r)
{
    if (l >= r) return;

    int i = l-1 , j = r , x = q[r];
    for(int j = l; j < r; j++){
        if(q[j]<=x){
            i++;
            swap(q[i],q[j]);
        }
    }
    swap(q[i+1],q[r]);
    quick_sort(q, l, i), quick_sort(q, i+2, r);
}

该方案为算法导论的标准方案,

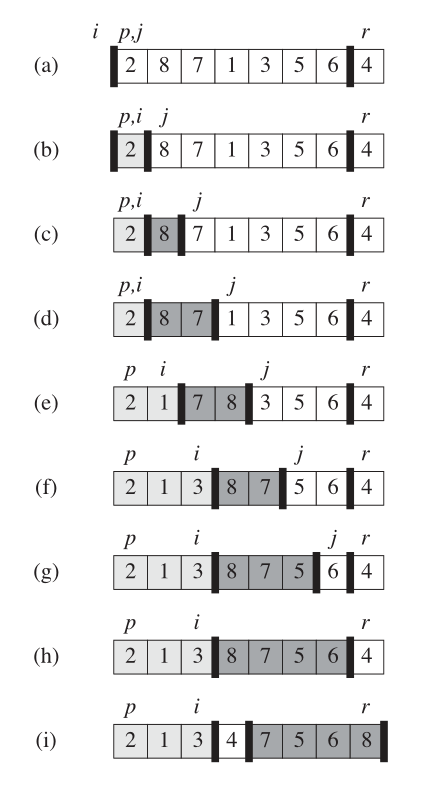
其中心思想是: l_{i**始终维护一个**<=pivot**的长度，而**j}r-1则维护一个>=pivot的长度，一旦q[j]<=x，立即执行i+1,此时i已经指向了第一个j~r-1的数，也就是第一个大于x的数，这时，交换q[j]与q[i]。 说明白点实际上就是将下图黑色区域（>x的划分）的第一个数与如今j遍历出来的 <x的数交换，然后将i的范围扩大，包容进去。

此循环结束之后，i为<x集合中最大的元素，此时只需要交换i+1也就是划分(j~r-1)中的第一个元素即可。这样一次划分就结束了。

这里有个很漂亮的边界处理，就是 i 初值指向l-1

注意：若是全顺序或者全逆序的情况，该算法会退化成O(n^2)，处理该情况需使用随机化方案，其实也就是每次排序前将一个序列中随机的值与pivot交换位置，使pivot为序列中的随机数
引入随机化

void quick_sort(int q[], int l, int r)
{
    if (l >= r) return;

    int flag = (rand() % (r - l)) + l;
    cout << q[flag]<<endl;
    swap(q[r], q[flag]);
    int i = l - 1, j = r, x = q[r];
    for (int j = l; j < r; j++) {
        if (q[j] <= x) {
            i++;
            swap(q[i], q[j]);
        }
    }
    swap(q[i + 1], q[r]);
    quick_sort(q, l, i), quick_sort(q, i + 2, r);

}

2）双向划分

void quick_sort(int q[], int l, int r) {
    if (l >= r) return;

    int x = q[l + r >> 1], i = l - 1, j = r + 1; 
    while (i < j) {
        do i ++ ; while (q[i] < x);
        do j -- ; while (q[j] > x);
        if (i < j) swap(q[i], q[j]);
    }
    
    quick_sort(q, l, j);
    quick_sort(q, j + 1, r);

}

关于算法分析与设计，参考算法导论，里面写的非常好。

例题：

786.第k个数

找出一个序列里排第n个的元素，序号从0开始

int n;
int quick_find(int q[], int l, int r){
    
    if(l==r) return q[l];
    int i = l-1, x = q[r];
    for(int j = l; j<r; j++){
        if(q[j]<=x){
            i++;
            swap(q[i],q[j]);
        }
    }
    
     swap(q[i+1],q[r]);
    
     //二分思想
     if(n==(i+1)) return q[i+1];
     if(n<(i+1)) return quick_find(q,l,i);
     if(n>(i+1)) quick_find(q,i+2,r);

}

应用了快排和二分思想。

该题有两个递归出口:

1.if(l==r) return q[l];
2.if(n==(i+1)) return q[i+1];

1.当l==r时，代表已经走完所有快速选择，之前没有在2出口出来就证明所要值一定在l==r处

2.当n==(i+1)，证明现在快排所插入的值就是索要的值，直接返回，回溯即可。后面的递归也不再需要了。

时间复杂度分析：n+n/2+n/4+n/8 ......<2n 因此时间复杂度为：O（n）