刷题--DFS--823.排列

DFS

823.排列

给定一个整数n，将数字1~n排成一排，将会有很多种排列方法。

现在，请你按照字典序将所有的排列方法输出。

输入格式

共一行，包含一个整数n。

输出格式

按字典序输出所有排列方案，每个方案占一行。

数据范围

1≤n≤91≤n≤9

输入样例：

3

输出样例：

1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1

思维过程：

​ 1.画出递归数

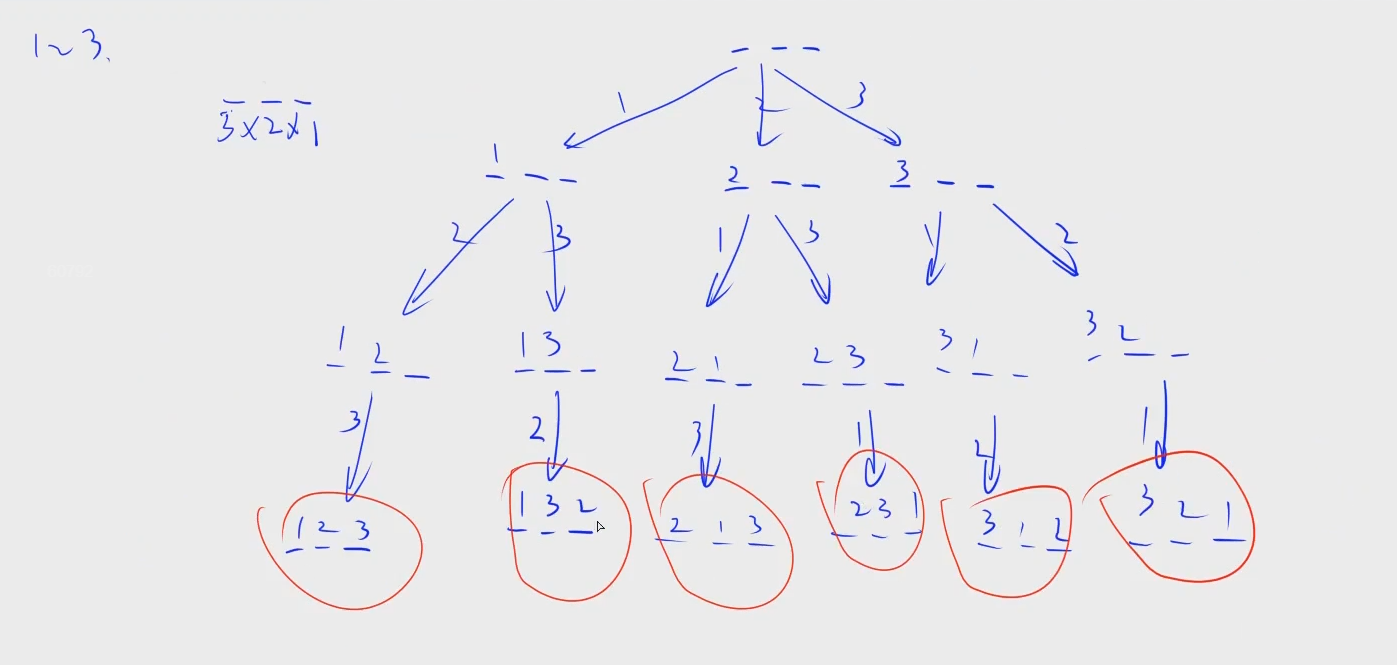
2.思考递边界与如何递归出该树：

​ 1）每层的父节点有n个分支

​ 2）树高为n

​ 3）放置数值时候，子节点是无法再次放置同样的数值的，所以需要设置一个标识 bool state[n]。如1_ _，放置了1之后，就在state数组里i=1的值设为true，代表已经用过。值得思考的是，在递归树中，子节点返回父节点的时候，得将设置的true恢复为false. 如 1_ _，返回后，就得将state[1]置为false,因为在2_ _这个递归中，1是可以被使用的。 以下是代码：

#include <iostream>
#include <memory.h>
using namespace std;

//代表数组的长度，同时也是递归树的高度
int n;
//保存值的数组
int s[10];
//保存了哪些数据已经用过了，下标代表数据，值代表是否用过
bool state[10];
void dfs(int n1) {
    //边界,说明已经排列完了一次
    if (n1 == n) {
        for (int i = 0; i < n; i++) cout << s[i]+1<<" ";
        cout << endl;
        return;
    }

    for (int i = 0; i < n; i++) {
         //说明未被使用过
        if (state[i] == false) {
            //进行s填充，并将相应标志位置为true
            s[n1] = i; 
            state[i] = true;
            //进行下一次dfs
            dfs(n1 + 1);
            //回到上一层后，将原来修改为true的state恢复现场为false
            state[i] = false;
        }       
    }
}

int main() {
    cin >> n;
    dfs(0);
}