【BJOI2014】大融合【LCT】
闲着没事写篇题解
LCT维护子树的模板题
树链剖分中,子树可以用dfs序维护。但LCT你总不可能动态维护dfs序啊
LCT之所以不能直接维护子树,是因为LCT只能维护它的重儿子。我们把这棵子树称为重子树。
对于其他子树,我们称为轻子树。轻子树只会储存父节点,要不试试在跑fa的时候顺便维护轻子树?
以此题为例,设s[i]为整棵子树的大小,si[i]为虚子树大小
这里的虚子树指所有虚边连向它的儿子的大小(即s)的和
不难看出,我们询问x,y时
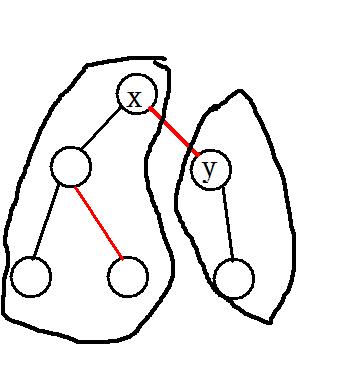
实际上是求(si[x]+1)(si[y]+1)
如何维护s和si?
我们发现,只有当改变了树的形态的时候,才会对s和si产生影响
access:会改变。直接在接头的时候顺便改一下
void access(int x)
{
for (int y=0;x;y=x,x=fa[x])
{
splay(x);
si[x]+=s[ch[x][1]];
si[x]-=s[ch[x][1]=y];
pushup(x);
}
}
makeroot:虽然改了,其实只是改了下顺序,access和splay里面会改
split:没有,下一个
link和cut:link把父亲的si加一下,cut把父亲的s和si都减一下
(实际上就是直接调用了fa或ch的函数)
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cctype>
#define MAXN 100005
using namespace std;
namespace Splay
{
int ch[MAXN][2],fa[MAXN];
int rv[MAXN];
int si[MAXN],s[MAXN];
void pushup(int x)
{
s[x]=s[ch[x][0]]+s[ch[x][1]]+si[x]+1;
}
void pushr(int x)
{
swap(ch[x][0],ch[x][1]);
rv[x]^=1;
}
void pushdown(int x)
{
if (rv[x])
{
if (ch[x][0]) pushr(ch[x][0]);
if (ch[x][1]) pushr(ch[x][1]);
rv[x]=0;
}
}
bool isroot(int x)
{
return ch[fa[x]][0]!=x&&ch[fa[x]][1]!=x;
}
bool get(int x)
{
return ch[fa[x]][1]==x;
}
void rotate(int x)
{
int y=fa[x],z=fa[y];
int l=get(x),r=l^1;
int w=ch[x][r];
if (!isroot(y))
ch[z][get(y)]=x;
ch[x][r]=y;
ch[y][l]=w;
if (w)
fa[w]=y;
fa[y]=x;
fa[x]=z;
pushup(y);
pushup(x);
}
int q[MAXN],top;
void splay(int x)
{
q[top=1]=x;
for (int i=x;!isroot(i);i=fa[i])
q[++top]=fa[i];
for (int i=top;i>=1;i--)
pushdown(q[i]);
while (!isroot(x))
{
int y=fa[x];
if (!isroot(y))
{
if (get(x)==get(y))
rotate(y);
else
rotate(x);
}
rotate(x);
}
pushup(x);
}
}
using namespace Splay;
namespace LCT
{
void access(int x)
{
for (int y=0;x;y=x,x=fa[x])
{
splay(x);
si[x]+=s[ch[x][1]];
si[x]-=s[ch[x][1]=y];
pushup(x);
}
}
void evert(int x)
{
access(x);
splay(x);
pushr(x);
}
void split(int x,int y)
{
evert(x);
access(y);
splay(y);
}
void link(int x,int y)
{
split(x,y);
si[fa[x]=y]+=s[x];
pushup(y);
}
}
using namespace LCT;
inline int read()
{
int ans=0;
char c=getchar();
while (!isdigit(c))
c=getchar();
while (isdigit(c))
ans=(ans<<3)+(ans<<1)+(c^48),c=getchar();
return ans;
}
inline char getalpha()
{
char c=getchar();
while (!isalpha(c))
c=getchar();
return c;
}
int main()
{
int n,q;
n=read(),q=read();
for (int i=1;i<=n;i++)
s[i]=1;
while (q--)
{
char c=getalpha();
int x,y;
x=read(),y=read();
if (c=='A')
link(x,y);
else
{
split(x,y);
printf("%I64d\n",(long long)(si[x]+1)*(si[y]+1));
}
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号