Python机器学习算法 — 关联规则（Apriori、FP-growth）
关联规则 -- 简介
关联规则挖掘是一种基于规则的机器学习算法，该算法可以在大数据库中发现感兴趣的关系。它的目的是利用一些度量指标来分辨数据库中存在的强规则。也即是说关联规则挖掘是用于知识发现，而非预测，所以是属于无监督的机器学习方法。
Apriori算法是一种挖掘关联规则的频繁项集算法，其核心思想是通过候选集生成和情节的向下封闭检测两个阶段来挖掘频繁项集。
关联规则的一般步骤:
1、找到频繁集；
2、在频繁集中通过可信度筛选获得关联规则。
关联规则应用：
1、Apriori算法应用广泛，可用于消费市场价格分析，猜测顾客的消费习惯，比如较有名的“尿布和啤酒”的故事；
2、网络安全领域中的入侵检测技术；
3、可用在用于高校管理中，根据挖掘规则可以有效地辅助学校管理部门有针对性的开展贫困助学工作；
4、也可用在移动通信领域中，指导运营商的业务运营和辅助业务提供商的决策制定。
关联规则算法的主要应用是购物篮分析，是为了从大量的订单中发现商品潜在的关联。其中常用的一个算法叫Apriori先验算法。
关联规则 -- 概念
关联分析（Association Analysis）：在大规模数据集中寻找有趣的关系。
频繁项集（Frequent Item Sets）：经常出现在一块的物品的集合，即包含0个或者多个项的集合称为项集。
支持度（Support）：数据集中包含该项集的记录所占的比例，是针对项集来说的。
置信度（Confidence）：出现某些物品时，另外一些物品必定出现的概率，针对规则而言。
关联规则（Association Rules）：暗示两个物品之间可能存在很强的关系。形如A->B的表达式，规则A->B的度量包括支持度和置信度
项集支持度：一个项集出现的次数与数据集所有事物数的百分比称为项集的支持度
支持度反映了A和B同时出现的概率，关联规则的支持度等于频繁集的支持度。
项集置信度：包含A的数据集中包含B的百分比
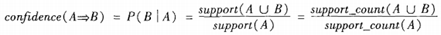
置信度反映了如果交易中包含A，则交易包含B的概率。也可以称为在A发生的条件下，发生B的概率，成为条件概率。
只有支持度和置信度(可信度)较高的关联规则才是用户感兴趣的。
关联规则 --支持度和置信度
1、支持度(Support)
支持度揭示了A与B同时出现的概率。如果A与B同时出现的概率小，说明A与B的关系不大；如果A与B同时出现的非常频繁，则说明A与B总是相关的。
支持度: P(A∪B)，即A和B这两个项集在事务集D中同时出现的概率。
2、可信度（Confidence）
置信度揭示了A出现时，B是否也会出现或有多大概率出现。如果置信度度为100%，则A和B可以捆绑销售了。如果置信度太低，则说明A的出现与B是否出现关系不大。
置信度: P(B｜A)，即在出现项集A的事务集D中，项集B也同时出现的概率。
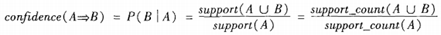
3、设定合理的支持度和置信度
对于某条规则：（A = a）−>（B = b）（support=30%,confident=60%）；其中support=30%表示在所有的数据记录中，同时出现A=a和B=b的概率为30%；confident=60%表示在所有的数据记录中，在出现A=a的情况下出现B=b的概率为60%，也就是条件概率。支持度揭示了A=a和B=b同时出现的概率，置信度揭示了当A=a出现时，B=b是否会一定出现的概率。
（1）如果支持度和置信度闭值设置的过高，虽然可以减少挖掘时间，但是容易造成一些隐含在数据中非频繁特征项被忽略掉，难以发现足够有用的规则；
（2）如果支持度和置信度闭值设置的过低，又有可能产生过多的规则，甚至产生大量冗余和无效的规则，同时由于算法存在的固有问题，会导致高负荷的计算量，大大增加挖掘时间。
关联规则 -- Apriori算法
Apriori算法简介
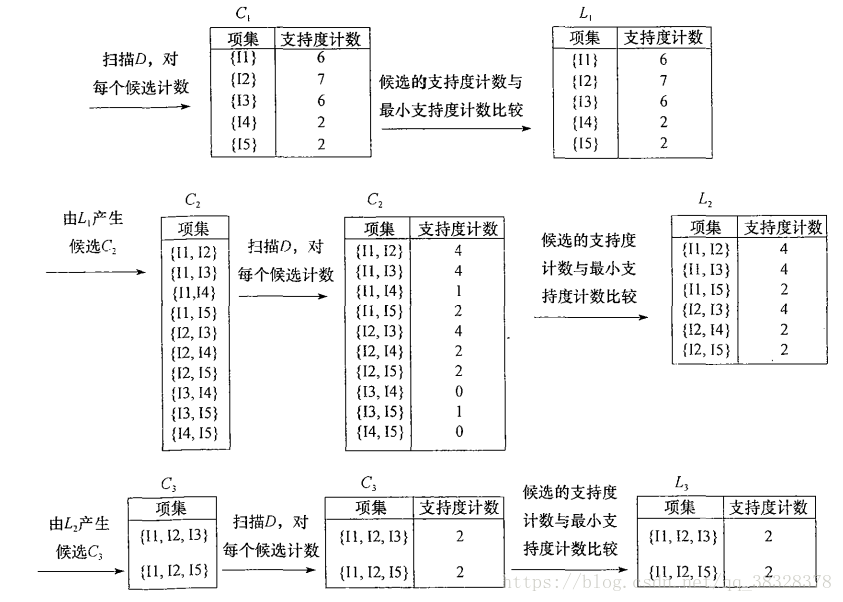
Apriori算法：使用候选项集找频繁项集
Apriori算法是一种最有影响的挖掘布尔关联规则频繁项集的算法。其核心是基于两阶段频集思想的递推算法。该关联规则在分类上属于单维、单层、布尔关联规则。在这里，所有支持度大于最小支持度的项集称为频繁项集，简称频集。
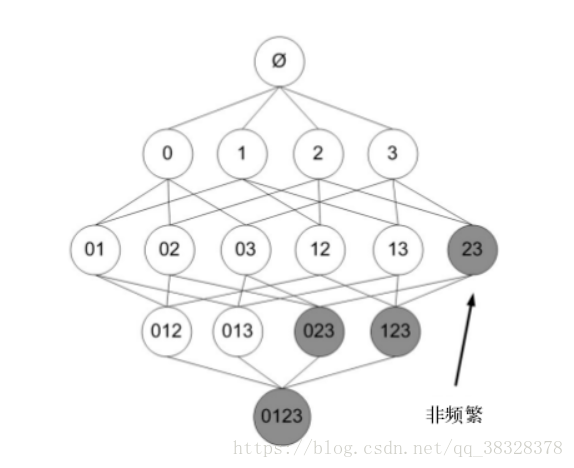
Apriori原理：如果某个项集是频繁的，那么它的所有子集也是频繁的。该定理的逆反定理为：如果某一个项集是非频繁的，那么它的所有超集（包含该集合的集合）也是非频繁的。Apriori原理的出现，可以在得知某些项集是非频繁之后，不需要计算该集合的超集，有效地避免项集数目的指数增长，从而在合理时间内计算出频繁项集。
在图中，已知阴影项集{2,3}是非频繁的。利用这个知识，我们就知道项集{0,2,3}，{1,2,3}以及{0,1,2,3}也是非频繁的。也就是说，一旦计算出了{2,3}的支持度，知道它是非频繁的后，就可以紧接着排除{0,2,3}、{1,2,3}和{0,1,2,3}。
算法思想
①找出所有的频集，这些项集出现的频繁性至少和预定义的最小支持度一样。
②由频集产生强关联规则，这些规则必须满足最小支持度和最小可信度。
③使用第1步找到的频集产生期望的规则，产生只包含集合的项的所有规则，其中每一条规则的右部只有一项，这里采用的是中规则的定义。
④一旦这些规则被生成，那么只有那些大于用户给定的最小可信度的规则才被留下来。为了生成所有频集，使用了递推的方法。
算法步骤
Ariori算法有两个主要步骤：
1、连接：（将项集进行两两连接形成新的候选集）
利用已经找到的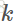
个项的频繁项集
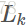，通过两两连接得出候选集
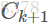，注意进行连接的
，
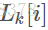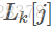，必须有
个属性值相同，然后另外两个不同的分别分布在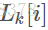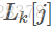，中，这样的求出的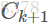为
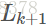的候选集。
2、剪枝：（去掉非频繁项集）
候选集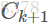中的并不都是频繁项集，必须剪枝去掉，越早越好以防止所处理的数据无效项越来越多。只有当子集都是频繁集的候选集才是频繁集，这是剪枝的依据
代码实现
#Apriori算法实现
from numpy import *
def loadDataSet():
return [[1, 3, 4], [2, 3, 5], [1, 2, 3, 5], [2, 5]]
# 获取候选1项集，dataSet为事务集。返回一个list，每个元素都是set集合
def createC1(dataSet):
C1 = [] # 元素个数为1的项集（非频繁项集，因为还没有同最小支持度比较）
for transaction in dataSet:
for item in transaction:
if not [item] in C1:
C1.append([item])
C1.sort() # 这里排序是为了，生成新的候选集时可以直接认为两个n项候选集前面的部分相同
# 因为除了候选1项集外其他的候选n项集都是以二维列表的形式存在，所以要将候选1项集的每一个元素都转化为一个单独的集合。
return list(map(frozenset, C1)) #map(frozenset, C1)的语义是将C1由Python列表转换为不变集合（frozenset，Python中的数据结构）
# 找出候选集中的频繁项集
# dataSet为全部数据集，Ck为大小为k（包含k个元素）的候选项集，minSupport为设定的最小支持度
def scanD(dataSet, Ck, minSupport):
ssCnt = {} # 记录每个候选项的个数
for tid in dataSet:
for can in Ck:
if can.issubset(tid):
ssCnt[can] = ssCnt.get(can, 0) + 1 # 计算每一个项集出现的频率
numItems = float(len(dataSet))
retList = []
supportData = {}
for key in ssCnt:
support = ssCnt[key] / numItems
if support >= minSupport:
retList.insert(0, key) #将频繁项集插入返回列表的首部
supportData[key] = support
return retList, supportData #retList为在Ck中找出的频繁项集（支持度大于minSupport的），supportData记录各频繁项集的支持度
# 通过频繁项集列表Lk和项集个数k生成候选项集C(k+1)。
def aprioriGen(Lk, k):
retList = []
lenLk = len(Lk)
for i in range(lenLk):
for j in range(i + 1, lenLk):
# 前k-1项相同时，才将两个集合合并，合并后才能生成k+1项
L1 = list(Lk[i])[:k-2]; L2 = list(Lk[j])[:k-2] # 取出两个集合的前k-1个元素
L1.sort(); L2.sort()
if L1 == L2:
retList.append(Lk[i] | Lk[j])
return retList
# 获取事务集中的所有的频繁项集
# Ck表示项数为k的候选项集，最初的C1通过createC1()函数生成。Lk表示项数为k的频繁项集，supK为其支持度，Lk和supK由scanD()函数通过Ck计算而来。
def apriori(dataSet, minSupport=0.5):
C1 = createC1(dataSet) # 从事务集中获取候选1项集
D = list(map(set, dataSet)) # 将事务集的每个元素转化为集合
L1, supportData = scanD(D, C1, minSupport) # 获取频繁1项集和对应的支持度
L = [L1] # L用来存储所有的频繁项集
k = 2
while (len(L[k-2]) > 0): # 一直迭代到项集数目过大而在事务集中不存在这种n项集
Ck = aprioriGen(L[k-2], k) # 根据频繁项集生成新的候选项集。Ck表示项数为k的候选项集
Lk, supK = scanD(D, Ck, minSupport) # Lk表示项数为k的频繁项集，supK为其支持度
L.append(Lk);supportData.update(supK) # 添加新频繁项集和他们的支持度
k += 1
return L, supportData
if __name__=='__main__':
dataSet = loadDataSet() # 获取事务集。每个元素都是列表
# C1 = createC1(dataSet) # 获取候选1项集。每个元素都是集合
# D = list(map(set, dataSet)) # 转化事务集的形式，每个元素都转化为集合。
# L1, suppDat = scanD(D, C1, 0.5)
# print(L1,suppDat)
L, suppData = apriori(dataSet,minSupport=0.7)
print(L,suppData)关联规则 -- FP树频集算法
算法简介
在关联分析中，频繁项集的挖掘最常用到的就是Apriori算法。Apriori算法是一种先产生候选项集再检验是否频繁的“产生-测试”的方法。这种方法有种弊端：当数据集很大的时候，需要不断扫描数据集造成运行效率很低。
而FP-Growth算法就很好地解决了这个问题。它的思路是把数据集中的事务映射到一棵FP-Tree上面，再根据这棵树找出频繁项集。FP-Tree的构建过程只需要扫描两次数据集。
算法步骤
FP-growth算法发现频繁项集的基本过程如下：
①构建FP树；
②从FP树中挖掘频繁项集；
实现流程
输入：数据集、最小值尺度
输出：FP树、头指针表
- 1、遍历数据集，统计各元素项出现次数，创建头指针表
- 2、移除头指针表中不满足最小值尺度的元素项
- 3、第二次遍历数据集，创建FP树。对每个数据集中的项集：
- 3.1 初始化空FP树
- 3.2 对每个项集进行过滤和重排序
- 3.3 使用这个项集更新FP树，从FP树的根节点开始：
- 3.3.1 如果当前项集的第一个元素项存在于FP树当前节点的子节点中，则更新这个子节点的计数值
- 3.3.2 否则，创建新的子节点，更新头指针表
- 3.3.3 对当前项集的其余元素项和当前元素项的对应子节点递归3.3的过程
算法详解
1、用FP树编码数据集
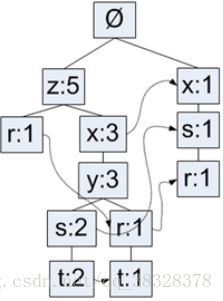
FP-growth算法将数据存储在一个称为FP树的紧凑数据结构中，它与计算机科学中的其他树的结构类似，但是它通过链接来链接相似元素，被连起来的元素可以看做一个链表，如下图：
图1--FP树的结构示意图
FP树会存储项集出现的频率，每个项集都会以路径的形式存储在树中，存在相似元素的集合会共享树的一部分。只有当集合之间完全不同时树才会分叉，树节点上给出集合中单个元素及其在序列中出现的次数，路径会给出该序列的出现次数。
相似项之间的链接即节点链接，用于快速发现相似项的位置，下面的例子：
图2--用于发现图1中FP树的事务数据样例
第一列是事务的ID，第二列是事务中的元素项，在图1中z出现了5次，而{r,z}项支出项了一次，所以z一定自己本身或者和其他的符号一起出现了4次，而由图1同样可知：集合{t,s,y,x,z}出现了2次，集合{t,r,y,x,z}出现了1次，所以z一定本身出现了1次。看了图2可能会有疑问，为什么在图1中没有p,q,w,v等元素呢？这是因为通常会给所有的元素设置一个阈度值（Apriori里的支持度），低于这个阈值的元素不加以研究。暂时不理解没关系，看了下面的内容可能会对这一段的内容有比较好的理解。
1.1、构建FP树
构建FP树是算法的第一步，在FP树的基础之上再对频繁项集进行挖掘。为了构建FP树，要对数据集扫描两次，第一次对所有元素项出现次数进行计数，记住如果一个元素不是频繁的，那么包含这个元素的超集也不是频繁的，所以不需要考虑这些超集，第二遍的扫描只考虑那些频繁元素。
除了图1给出的FP树之外，还需要一个头指针表来指向给定类型的第一个实例。利用头指针表可以快速访问FP树中一个给定类型的所有元素，发现相似元素项，如下图所示：
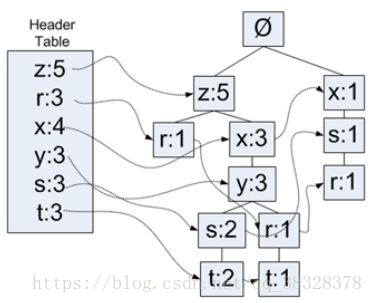
图3--带头指针的FP树
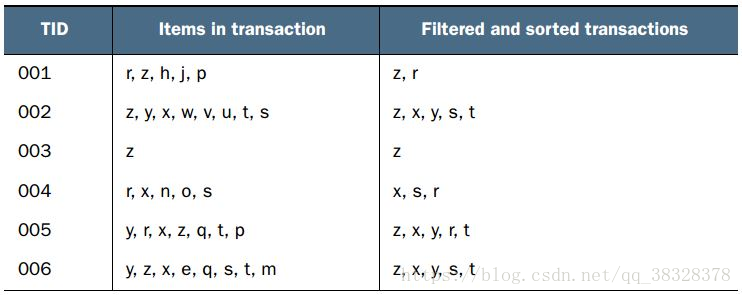
头指针表的数据结构是字典，除了存放头指针元素之外，还可以存放FP中每类元素的个数。第一次遍历数据集得到每个元素项出现的频率，接下来去掉不满足最小值支持度的元素项，在接下来就可以创建FP树了，构建时，将每个项集添加到一个已经存在的路径中，如果该路径不存在，则创建一个新的路径。每个事务都是一个无序的集合，然而在FP树中相同项只会出现一次，{x,y,z}和{y,z,x}应该在同一个路径上，所以在将集合添加到树之前要对每个集合进行排序，排序是基于各个元素出现的频率来进行的，使用图3头指针表中单个元素的出现值，对图2中的数据进行过滤，重排后的新数据如下：
图4--移除非频繁项，重新排序后的事务表
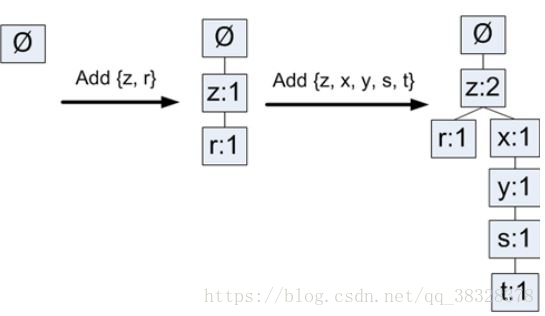
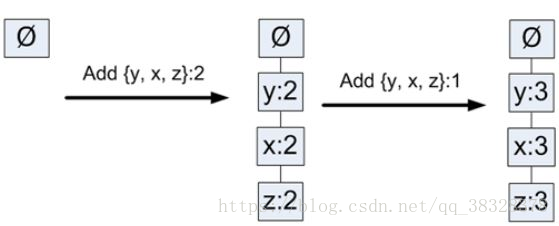
现在，就可以构建FP树了，从空集开始，向其中不断添加频繁项集。过滤，排序后的事务依次添加到树中，如果树中已有现有元素，则增加该元素的值；如果元素不存在，则添加新分枝。图4中事务表前两条事务添加的过程如下图所示：
图5--FP构建过程示例图
2、从FP树中挖掘频繁项
有了FP树之后就可以抽取频繁项集了，思想与Apriori算法大致一样，从单元素项集开始，逐步构建更大的集合，只不过不需要原始的数据集了。从FP树中抽取频繁项集的三个基本步骤：
1）从FP树中获得条件模式基；
2）利用条件模式基，构建一个条件FP树；
3）迭代重复步骤（1）（2）直到树只包含一个元素项为止
2.1抽取条件模式基
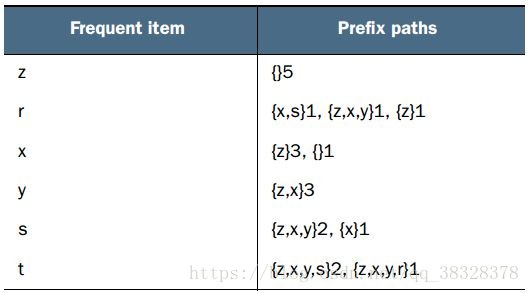
条件模式基是以所查找元素项为结尾的路径集合，每一条路径包含一条前缀路径和结尾元素，图3中，符号r的前缀路径有{x,s}、{z,x,y}和{z}，每一条前缀路径都与一个数据值关联，这个值等于路径上r的数目，下表中列出单元素频繁项的所有前缀路径。
图6--每个频繁项的前缀路径
前缀路径将被用于构建条件FP树。为了获得这些路径，可以对FP树进行穷举式搜索，直到获得想要的频繁项为止，但可以使用一个更为有效的方法加速搜索过程。可以用先前的头指针表来创建一种更为有效的方法，头指针表中包含相同类型元素链表的起始指针。一旦到达了每一个元素项，就可以上溯这棵树直到根节点为止。
2.2、创建条件FP树
对于每一个频繁项，都要创建一个条件FP树，将上面的条件模式基作为输入，通过相同的建树方法来构建这些条件树，然后递归地发现频繁项、发现条件模式基，以及发现另外的条件树。举个例子，假定为频繁项t创建一个条件FP树，然后对{t,y}，{t,x}、...重复该过程。元素项t的条件FP树的构建过程如下：
图7
s，r虽然是条件模式基的一部分，且单独看都是频繁项，但是在t的条件树中，他却是不频繁的，分别出现了2次和一次，小于阈值3，所以{t,r}，{t,s}不是频繁的。接下来对集合{t,z}，{t,x}，{t,y}来挖掘对应的条件树，会产生更复杂的频率项集，该过程重复进行，直到条件树中没有元素 为止，停止。
代码实现
# FP树类
class treeNode:
def __init__(self, nameValue, numOccur, parentNode):
self.name = nameValue #节点元素名称，在构造时初始化为给定值
self.count = numOccur # 出现次数，在构造时初始化为给定值
self.nodeLink = None # 指向下一个相似节点的指针，默认为None
self.parent = parentNode # 指向父节点的指针，在构造时初始化为给定值
self.children = {} # 指向子节点的字典，以子节点的元素名称为键，指向子节点的指针为值，初始化为空字典
# 增加节点的出现次数值
def inc(self, numOccur):
self.count += numOccur
# 输出节点和子节点的FP树结构
def disp(self, ind=1):
print(' ' * ind, self.name, ' ', self.count)
for child in self.children.values():
child.disp(ind + 1)
# =======================================================构建FP树==================================================
# 对不是第一个出现的节点，更新头指针块。就是添加到相似元素链表的尾部
def updateHeader(nodeToTest, targetNode):
while (nodeToTest.nodeLink != None):
nodeToTest = nodeToTest.nodeLink
nodeToTest.nodeLink = targetNode
# 根据一个排序过滤后的频繁项更新FP树
def updateTree(items, inTree, headerTable, count):
if items[0] in inTree.children:
# 有该元素项时计数值+1
inTree.children[items[0]].inc(count)
else:
# 没有这个元素项时创建一个新节点
inTree.children[items[0]] = treeNode(items[0], count, inTree)
# 更新头指针表或前一个相似元素项节点的指针指向新节点
if headerTable[items[0]][1] == None: # 如果是第一次出现，则在头指针表中增加对该节点的指向
headerTable[items[0]][1] = inTree.children[items[0]]
else:
updateHeader(headerTable[items[0]][1], inTree.children[items[0]])
if len(items) > 1:
# 对剩下的元素项迭代调用updateTree函数
updateTree(items[1::], inTree.children[items[0]], headerTable, count)
# 主程序。创建FP树。dataSet为事务集，为一个字典，键为每个事物，值为该事物出现的次数。minSup为最低支持度
def createTree(dataSet, minSup=1):
# 第一次遍历数据集，创建头指针表
headerTable = {}
for trans in dataSet:
for item in trans:
headerTable[item] = headerTable.get(item, 0) + dataSet[trans]
# 移除不满足最小支持度的元素项
keys = list(headerTable.keys()) # 因为字典要求在迭代中不能修改，所以转化为列表
for k in keys:
if headerTable[k] < minSup:
del(headerTable[k])
# 空元素集，返回空
freqItemSet = set(headerTable.keys())
if len(freqItemSet) == 0:
return None, None
# 增加一个数据项，用于存放指向相似元素项指针
for k in headerTable:
headerTable[k] = [headerTable[k], None] # 每个键的值，第一个为个数，第二个为下一个节点的位置
retTree = treeNode('Null Set', 1, None) # 根节点
# 第二次遍历数据集，创建FP树
for tranSet, count in dataSet.items():
localD = {} # 记录频繁1项集的全局频率，用于排序
for item in tranSet:
if item in freqItemSet: # 只考虑频繁项
localD[item] = headerTable[item][0] # 注意这个[0]，因为之前加过一个数据项
if len(localD) > 0:
orderedItems = [v[0] for v in sorted(localD.items(), key=lambda p: p[1], reverse=True)] # 排序
updateTree(orderedItems, retTree, headerTable, count) # 更新FP树
return retTree, headerTable
# =================================================查找元素条件模式基===============================================
# 直接修改prefixPath的值，将当前节点leafNode添加到prefixPath的末尾，然后递归添加其父节点。
# prefixPath就是一条从treeNode（包括treeNode）到根节点（不包括根节点）的路径
def ascendTree(leafNode, prefixPath):
if leafNode.parent != None:
prefixPath.append(leafNode.name)
ascendTree(leafNode.parent, prefixPath)
# 为给定元素项生成一个条件模式基（前缀路径）。basePet表示输入的频繁项，treeNode为当前FP树中对应的第一个节点
# 函数返回值即为条件模式基condPats，用一个字典表示，键为前缀路径，值为计数值。
def findPrefixPath(basePat, treeNode):
condPats = {} # 存储条件模式基
while treeNode != None:
prefixPath = [] # 用于存储前缀路径
ascendTree(treeNode, prefixPath) # 生成前缀路径
if len(prefixPath) > 1:
condPats[frozenset(prefixPath[1:])] = treeNode.count # 出现的数量就是当前叶子节点的数量
treeNode = treeNode.nodeLink # 遍历下一个相同元素
return condPats
# =================================================递归查找频繁项集===============================================
# 根据事务集获取FP树和频繁项。
# 遍历频繁项，生成每个频繁项的条件FP树和条件FP树的频繁项
# 这样每个频繁项与他条件FP树的频繁项都构成了频繁项集
# inTree和headerTable是由createTree()函数生成的事务集的FP树。
# minSup表示最小支持度。
# preFix请传入一个空集合（set([])），将在函数中用于保存当前前缀。
# freqItemList请传入一个空列表（[]），将用来储存生成的频繁项集。
def mineTree(inTree, headerTable, minSup, preFix, freqItemList):
# 对频繁项按出现的数量进行排序进行排序
sorted_headerTable = sorted(headerTable.items(), key=lambda p: p[1][0]) #返回重新排序的列表。每个元素是一个元组，[（key,[num,treeNode],()）
bigL = [v[0] for v in sorted_headerTable] # 获取频繁项
for basePat in bigL:
newFreqSet = preFix.copy() # 新的频繁项集
newFreqSet.add(basePat) # 当前前缀添加一个新元素
freqItemList.append(newFreqSet) # 所有的频繁项集列表
condPattBases = findPrefixPath(basePat, headerTable[basePat][1]) # 获取条件模式基。就是basePat元素的所有前缀路径。它像一个新的事务集
myCondTree, myHead = createTree(condPattBases, minSup) # 创建条件FP树
if myHead != None:
# 用于测试
print('conditional tree for:', newFreqSet)
myCondTree.disp()
mineTree(myCondTree, myHead, minSup, newFreqSet, freqItemList) # 递归直到不再有元素
# 生成数据集
def loadSimpDat():
simpDat = [['r', 'z', 'h', 'j', 'p'],
['z', 'y', 'x', 'w', 'v', 'u', 't', 's'],
['z'],
['r', 'x', 'n', 'o', 's'],
['y', 'r', 'x', 'z', 'q', 't', 'p'],
['y', 'z', 'x', 'e', 'q', 's', 't', 'm']]
return simpDat
# 将数据集转化为目标格式
def createInitSet(dataSet):
retDict = {}
for trans in dataSet:
retDict[frozenset(trans)] = 1
return retDict
if __name__=='__main__':
minSup =3
simpDat = loadSimpDat() # 加载数据集
initSet = createInitSet(simpDat) # 转化为符合格式的事务集
myFPtree, myHeaderTab = createTree(initSet, minSup) # 形成FP树
# myFPtree.disp() # 打印树
freqItems = [] # 用于存储频繁项集
mineTree(myFPtree, myHeaderTab, minSup, set([]), freqItems) # 获取频繁项集
print(freqItems) # 打印频繁项集作者：ls秦
本文版权归作者和博客园共有，欢迎转载，但未经作者同意必须保留此段声明，且在文章页面明显位置给出原文连接，否则保留追究法律责任的权利.
