[复习资料]关于最优化类 dp 的优化
关于最优化类 dp 的优化
复习一下三种最优化类 dp 的优化方式。
决策单调性优化
普通类型
在序列上面的 dp ,设最优决策点依次为 \(g_{1,\dots,n}\) ,如果满足 \(g_i\le g_{i+1}\) ,那么可以以此优化 dp 的转移。
具体实现两种方式(均为 \(\mathcal O(n\log_2n)\) ):
- 如果现在需要求出来的 dp 值和之前需要求出来的 dp 值没有关系,可以使用分治的方法。
- 如果现在需要求出来的 dp 值和之前需要求出来的 dp 值有关系,可以使用维护最优决策点相同的一段的方法。
四边形不等式
在区间上面的 dp ,转移方程如果是类似这样的:
\[dp(l,r)=\min_{k=l}^{r-1}(dp(l,k)+dp(k+1,r))+\operatorname{val}(l,r)
\]
设 \(g(l,r)\) 表示最优决策点,如果满足(四边形不等式):
\[\operatorname{val}(l,r)+\operatorname{val}(l-1,r+1)\le \operatorname{val}(l,r+1)+\operatorname{val}(l-1,r)
\]
可以通过下图简易记忆(认为 \(\operatorname{val}(l,r)\) 是 \(l\) 与 \(r\) 之间的距离):
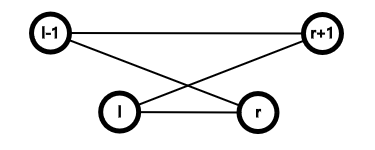
那么有 \(g(l,r-1)\le g(l,r)\le g(l+1,r)\) ,由此减小枚举量。
斜率优化
两种可以斜率优化的情况:
- 式子可以转化为最优化两点间直线的截距。
- 式子可以转化为最优化两点间直线的斜率。
使用数据结构维护凸包。
下面的表格是第一种斜率优化时针对题目特点用到的数据结构。
| 加入点的某一维度单调 | 加入点的两维都不单调 | |
|---|---|---|
| 查询的斜率单调 | 单调队列/单调栈+直接弹掉 | 平衡树+二分 |
| 查询的斜率不单调 | 单调队列/单调栈+二分 | 平衡树+二分 |
带权二分
给定一个上/下凸函数,可以求出这个函数加上一个正比例函数时的函数值取到最大/小值的点,求某个位置的函数值。
二分正比例函数的斜率,根据求出的最值点来判断斜率需要变大还是变小。
往往可以把 dp 时需要记录的一维优化成一个 \(\log_2\) 。
一般可以用费用流求解的问题都是凸函数。


