板刷NOI
板刷NOI
刷 NOI 啊?这很好。但是刷多了人脑子就不清醒了,这人呢脑子一不清醒就不知道会干出什么事、写出什么代码来。
刷不太动啊啊啊啊啊。
NOI2016
算了, NOI2016 队线摸都摸不着,不写了23333333
day1
T1 优秀的拆分
T2 网格
T3 循环之美
day2
T1 区间
T2 国王饮水记
T3 旷野大计算
NOI2017
day1
T1 整数
极限得分: \(100\)
队爷 Imakf 讲过,用线段树维护这个数,线段树上面的叶子结点维护若干个二进制位,进位和退位通过线段树上面二分实现,时间复杂度为 \(\mathcal O(\frac{30}{w}n\log_2(\frac{30}{w}n))\) 。
T2 蚯蚓排队
极限得分: \(100\)
直接暴力存所有字符串就行了,字符串 hash 或者 AC 自动机都可以做,时间复杂度是 \(\mathcal O(nk+ck^2+\sum|s|)\) 。
T3 泳池
极限得分: \(100\)
给定危险区域求游泳场面积很好求,笛卡尔树的模板,不过答案是一个 \(\max()\) 的形式不好满足恰好的条件,所以用 \(\le K\) 的方案数减去 \(< K\) 的方案数, dp 的话就和普通的笛卡尔树 dp 差不多,设 \(f(i,j)\) 表示 \(i\) 个点形成的笛卡尔树,其中根的高度为 \(j\) 并且合法的方案数,那么转移方程就是:
前缀和一下:
其中 \(f(i,j)\) 有值当且仅当 \(i\times j\le K\) ,所以 \(j>0\) 时的 dp 状态数是 \(K\ln K\) 级别的,所以 \(j>0\) 时求出所有 dp 值的时间复杂度为 \(\mathcal O(K^2\ln K)\) 。
\(j=0\) 时显然就不可以暴力求解了,长度为 \(N\) 必然是由若干个 \(f(i,1),i\le K\) 拼起来的,设答案为 \(G_N\) ,那么可以得到递推式:
设 \(F_i=(1-q)f(i-1,1)\) ,剩下的就是常系数齐次线性递推的模板了,暴力卷积即可,时间复杂度为 \(\mathcal O(K^2\log_2 N)\) 。
day2
T1 游戏
极限得分: \(100\)
没有 x 就可以直接 2-SAT ,对于一个要求 \((i,h_i,j,h_j)\) , \(h_i\) 非法时啥事没有, \(h_j\) 非法时 \(i\) 的 \(h_i\) 号点向 \(i\) 的 \(h_i\oplus 1\) 号点连边,否则 \(i\) 的 \(h_i\) 号点向 \(j\) 的 \(h_j\) 号点连边, \(j\) 的 \(h_j\oplus 1\) 号点向 \(i\) 的 \(h_i\oplus 1\) 号点连边。
有 x 枚举 x 是 a 或者是 b 即可,正确性显然。
时间复杂度 \(\mathcal O(2^d(n+m))\) 。
T2 蔬菜
极限得分: \(100\)
最暴力直接费用流建模,前缀和优化建图,有多少蔬菜在哪一天馊掉就直接连边,边的数量就是 \(n\) 乘以天数的,也许可以过 60pts 。
稍微优化一下,类似美食节那样,没有用的边先不连,在跑费用流的过程中加上去,边的数量就是 \(n\) 的,可以过 80pts 。
发现这个图十分简单,费用流可以直接模拟,然后线段树加堆维护每一条边的流量模拟即可,可以过 100pts 。
设 \(D\) 表示天数,时间复杂度 \(\mathcal O(Dm\log_2 D)\) 。
另外一种方法是先把最后一天的答案求出来,然后倒着退回去,第 \(k\) 天没有馊掉的菜第 \(k-1\) 天肯定也没有馊,所以看当天卖出去的菜可不可以由前面更便宜的菜替代即可,时间复杂度 \(\mathcal O(Dn\log_2 D)\) ,而且还巨好写。
T3 分身术
极限得分: \(20\)
计算几何爬!!!
每次暴力求凸包 20pts ,正解不会。
NOI2018
day1
T1 归程
极限得分: \(100\)
dijkstra + kruskal 重构树。
时间复杂度 \(\mathcal O((n+m)\log_2 m+q\log_2 n)\) 。
T2 冒泡排序
极限得分: \(100\)
交换次数显然就是逆序对数量,设以 \(i\) 为端点的逆序对数量为 \(A_i\) ,那么必然有 \(|p_i-i|\le A_i\) ,交换次数为 \(\frac{1}{2}\sum_{i=1}^nA_i\) 要到达 \(\frac{1}{2}\sum_{i=1}^n|p_i-i|\) 的下界 \(|p_i-i|\) 必须要等于 \(A_i\) ,取到等号必须要满足 \(i\) 左边的数全小于 \(p_i\) 或者右边的数全大于 \(p_i\) ,也就是等价于 \(p\) 中最长下降子序列( lds )的长度要 \(\le 2\) 。
从左往右扫 \(p\) ,发现 \(1\sim n\) 这些数字只有三种状况:没出现过、以它为结尾的 lds 长度为 1 、以它为结尾的 lds 长度为 2 。
注意到 lds 长度为 2 的下面是不能有空位了, lds 长度为 1 的下面的空位必须从下到上一个一个填,所以只需要记录最上面连续空位的长度和空位总数即可确定总的填数的方案数。
设 \(f(i,j)\) 表示总空位数量为 \(i\) ,其中最上面连续空位长度为 \(j\) 的填数方案数,转移方程:
或者也可以写成:
其中当 \(i<j\) 时, \(f(i,j)=0\) 。
类似卡特兰数,不难得到 \(f(i,j)={i+j\choose i}-{i+j\choose i+1}\) 。
至于字典序严格大于某一个排列,枚举排列和给定排列的 lcp 即可。
时间复杂度 \(\mathcal O(\sum n)\) 。
T3 你的名字
极限得分: \(100\)
SAM + 线段树合并 + 2-pointers 。
时间复杂度 \(\mathcal O((|S|+\sum |T|)\log_2 |S|)\) 。
day2
这个 day2 compared with day1 怎么这么不可做啊啊啊啊啊。
T1 屠龙勇士
极限得分: \(100\)
扩展中国剩余定理求出解集,然后再找最小合法解即可。
需要注意的几点:
- 不要爆 long long 。
- \(ax\equiv b\pmod p \Leftrightarrow x\equiv \frac{b}{a}\pmod {\frac{p}{\gcd(p,a)}}\) 。
- 不要用 set ,用 multiset 。
时间复杂度根据实现两个 log 或者一个 log 。
T2 情报中心
极限得分: \(45\)
枚举路径判相交,时间复杂度 \(\mathcal O(m^2\log_2n)\) 或者 \(\mathcal O(m^2)\) 。 15pts
一条链直接按左端点排序然后瞎搞就可以了。 15pts
\(c_i=0\) 找到跨过每条边花费最小的两条链即可。 15pts
以上为 45pts 。
\(S_1\) 发现两条链相交必然是直上直下的链,考虑枚举相交链的下端点(即下图中的 \(z\) 结点)。
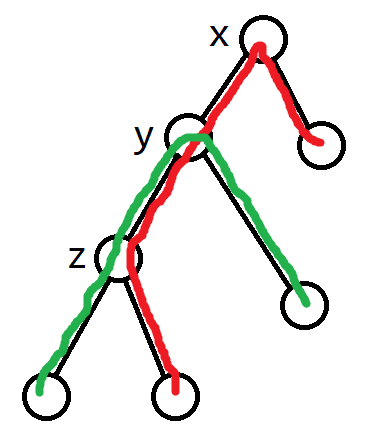
设 \(val\) 表示某一条情报方案经过的边的收益减去花费, \(val_g\) 和 \(val_r\) 分别表示绿色和红色, \(\operatorname{dep}(i)\) 表示 \(i\) 到根的边的收益之和,那么绿色和红色拼起来的总收益减总花费就是 \(val_g+val_r-\operatorname{dep}(z)+\max(\operatorname{dep}(x),\operatorname{dep}(y))\) ,由于加的是 \(\max()\) ,答案求的也是 \(\max()\) ,所以可以直接把 \(\max()\) 拆开分开算,还有一个要求就是红色和绿色要在 \(z\) 处分叉,这个可以通过在子树合并时算答案满足这个要求,剩下的就是线段树合并或者可删可并堆的事了。 15pts
\(S_2\) 发现两条链相交必然经过根(不过这好像没有用)。

红色绿色拼起来的答案为 \(val_g+val_r-\operatorname{dep}(y)-\operatorname{dep}(z)\) ,枚举 \(y\) ,合并子树的时候完全不太好算的样子,设红色端点分别为 \(R_1,R_2\) ,绿色端点分别为 \(G_1,G_2\) ,那么 \(\operatorname{dep}(z)=\frac{1}{2}(\operatorname{dep}(R_2)+\operatorname{dep}(G_2)-\operatorname{dis}(R_2,G_2))\) ,转化后要求的东西可以很简单地转化成两两点之间的距离最大值,这样只需要维护点集中的直径即可合并了。 20pts
正解 \(\approx S_1+S_2\) ,分两部分处理即可。 20pts
T3 多边形
极限得分: \(50\)
状压求哈密尔顿回路,时间复杂度 \(\mathcal O(2^nn^2)\) 。 20pts
\(K=1\) 时显然 dfs 序相邻的叶子一定是若干连续段一起走,很简单就可以得到一个点会被经过的条件,然后直接 dp 即可,时间复杂度 \(\mathcal O(n)\) 。 30pts
以上为 50pts 。
正解好像是爆搜所有接口,然后爆搜所有转移。。。
NOI2019
day1
T1 回家路线
极限得分: \(100\)
将上车和下车看作是两个事件,将所有事件按顺序排序,每个站点维护一个双端队列斜率优化 dp 即可。。。
时间复杂度 \(\mathcal O(n+m)\) 。
T2 机器人
极限得分: \(100\)
建出笛卡尔树,题面中的要求相当于是每个点的左右儿子子树大小之差小于等于 \(2\) ,暴力 dp 设 \(f(i,l,r)\) 表示考虑 \(l\sim r\) 这一段建出来的笛卡尔树其中根的高度为 \(i\) 的方案数,那么转移前缀和优化一下可以做到 \(\mathcal O(n^2B)\) (转移复杂度 \(\mathcal O(1)\) )的时间复杂度,预处理出要用的区间可以做到 \(\mathcal O(2047B)\) 。
复杂度需要和 \(B\) 无关,考虑对每一个值域区间 \([L,R]\) 分开依次处理,注意到区间 \([l,r]\) 最多只有 \(r-l+1\) 种不同的权值,可以统计一个区间恰好有多少种不同权值的方案数,假设有 \(k\) 种不同的权值,那么方案数乘以 \({R-L+1\choose k}\) 贡献过去就行了,这样 dp 的第一维最大就只是 \(n\) ,求恰好多少种不同权值方案数需要二项式反演或者其它方法(反正求出来的东西和要求的东西是一个组合数关系),这样的话时间复杂度为 \(\mathcal O(n^5)\) (外层枚举值域一个 \(n\) ,内层 dp \(n^3\) ,不过二项式反演什么的 \(n^4\) ),仅保留有用区间,时间复杂度降为 \(\mathcal O(2047n^2+435072n)\) (所有有用区间长度平方和为 \(435072\) ),勉强飘过。
以上为自己想法。
不过实际上不需要二项式反演,只要知道了二项式关系就可以得到 dp 值和它的第一维之间的关系其实是一个区间长度级别的多项式,所以直接插值就可以了。。。时间复杂度 \(\mathcal O(2047n^2)\) ,还可以降为 \(\mathcal O(14408n)\) (所有区间长度和为 \(14408\) )。
T3 序列
极限得分: \(100\)
\(a,b\) 一遍从大往小 sort 猛如虎,最大的 \(K-L\) 个数肯定选,剩下要选的是 \(L\) 对,这些对中的一些数如果已经选过了,那么造成的贡献其实是它后面的没有选的最近的一个数,所以可以这样费用流建模:
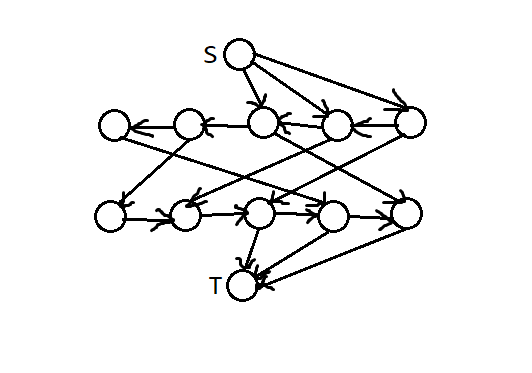
一波前缀,一波后缀,配对对应连边即可。(出了前缀后缀连边流量 inf 其它流量为 1 )
跑一遍费用流流 \(L\) 下即可。
显然上面到下面的一条边 \(u\to v\) 等价于 \(\max(u,K-L+1)\to \max(v,K-L+1)\) ,这样只有 \(K-L+1\) 可能有多条出边。
但是其实没有必要,注意到费用其实是排好序的,并且流量都是 1 ,所以以下两个图等价:

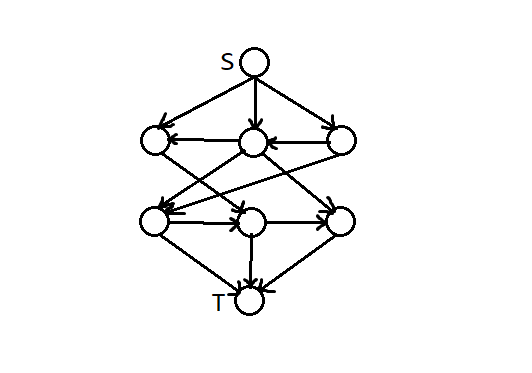
上下两张图有什么区别其实就是想说明很多条边只需要保留一条最优的边即可,于是用个堆或者桶之类的维护所有出边即可,需要注意用并查集去重,从左到右扫一遍就可以保留所有有用的边,然后一遍 sort 取前 \(L\) 大即可。
时间复杂度 \(\mathcal O(\sum n\log_2n)\) 。
day2
T1 弹跳
极限得分: \(100\)
在 Kdtree 上面跑 dijkstra 即可(维护最小值 + 区间取 min )。
时间复杂度 \(\mathcal O(m\sqrt{n}+n\log_2n)\) 。
T2 斗主地
极限得分: \(100\)
发现这个合并很神, \(n\) 张牌和 \(m\) 张牌合并就是等价于在 \({n+m\choose n}\) 种按顺序合并的方案中等概率选取一种合并方法合并。
一波推式子可以很容易得到一次合并后每一个位置对位置的贡献是多少,所以很容易做到 \(\mathcal O(n^2m)\) 。
\(n\le 100\) 并且所有 \(A_i\) 相同显然可以矩乘,时间复杂度 \(\mathcal O(n^3\log_2m)\) 。
然后好像就不可做了。。。还有一个没有用到的性质就是 \(f(i)=i\) 或者 \(f(i)=i^2\) ,这个肯定是突破口。
打表找规律发现当 \(f(i)=i\) 时答案是一次函数, \(f(i)=i^2\) 时答案是二次函数,然后拉插拉插拉插拉插拉插随便维护三个点值拉格朗日插值就行了。
证明鸽了(其实不会证)。
时间复杂度 \(\mathcal O(n+m+q)\) 。
T3 I 君的探险
极限得分: \(56\)
\(N(N-1)/2\) 次询问 \(N-1\) 次修改比较简单。 20pts
性质 A 整体二分找另一半。 16pts
性质 B 整体二分找父亲。 8pts
性质 C 二进制分组求相邻点异或和,暴力求一个点旁边的点就可以直接找了。 12pts
以上 56pts ,其它不会。
NOI2020
day1
T1 美食家
极限得分: \(100\)
矩乘。注意预处理矩阵 \(2^k\) 幂,然后用向量乘以矩阵。时间复杂度为 \(\mathcal O(n^2(n+k)\log_2 T)\) 。
T2 命运
极限得分: \(100\)
T3 时代的眼泪
极限得分: \(52\)
暴力 \(\mathcal O(nm\log_2 n)\) 。24pts
性质 A 莫队,同步赛的时候写的复杂度是 \(\mathcal O(m\sqrt{n}\log_2n)\) 的,可以过。16pts
性质 C 枚举每个非逆序对一个一个减掉就可以了。 12pts
以上 52pts 。
分块不会,不搞正解了。
day2
T1 制作菜品
极限得分: \(100\)
看到 \(m=n-1\) 想到树( \(n\) 个点 \(m\) 条边的连通图),一条树边表示一道菜品,树上面的一个结点表示一种原材料,树边连接着的两个结点表示一道菜品用哪两种原材料制作。
在树的形态确定的时候一道菜用哪两种原材料其实已经确定了,考虑随便以一个点为根,设一个点 \(u\) 的子树大小为 \(\operatorname{size}_u\) ,子树中所有原材料数量和为 \(\operatorname{sum}_u\) ,那么 \(u\) 和它父亲的连边中使用 \(u\) 的数量必定是 \(\operatorname{sum}_u-k(\operatorname{size}_u-1)\) ( \(u\) 整棵子树只能装下 \(k(\operatorname{size}_u-1)\) 这么多原材料啊,剩下的只能放在这一条边上面了),所以我们就可以得到一个限制 \(0\le \operatorname{sum}_u-k(\operatorname{size}_u-1)\le k\) ,或者说是 \(-k\le \sum\limits_{v\in \operatorname{subtree}_u}(d_v-k)\le 0\) 。
由此我们就已经可以构造了,先 \(d_i\gets d_i-k\) ,然后从小到大排序,从左往右扫一遍,将它后面第一个当前和大于等于 \(0\) 的作为它的父亲即可,正确性显然,同时也可以发现 \(m=n-1\) 时永远有解。
当 \(m>n-1\) 的时候就把 \(m\) 减成 \(n-1\) 就行了(每次找到一个质量大于等于 \(k\) 的原材料,根据鸽巢原理必然存在这样的原材料)。
当 \(m=n-2\) 时就想办法把 \(n\) 种原材料分成两个非空集合 \(S,T\) 满足 \(\sum\limits_{u\in S}(d_u-k)=\sum\limits_{u\in T}(d_u-k)=0\) ,然后分成两棵树搞就行了,通过背包 + bitset 来分集合。
时间复杂度 \(\sum(\frac{n^2k}{\omega}+m)\) 。
T2 超现实树
极限得分: \(40\)
特殊性质 4 ,每次三棵树合并就行了,或者每次分裂三棵树就行了。 可以拿到 40pts
以上 40pts ,其它不会做,没思维选手枯了。
T3 翻修道路
极限得分: \(0\)
被弦图整枯了。
啥也不会,爬了。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号