题解 [Code+#3]白金元首与莫斯科
题解 [Code+#3]白金元首与莫斯科
以下计算时间复杂度的时候认为 \(m\) 和 \(n\) 同阶。
题目分析
先不考虑求以每个格子为障碍物时的答案,如果仅仅只是求方案数应该如何求?
状压dp
使用朴素的状压dp,设 \(dp(i,j,sta)\) 表示已经确定了完全包含在前 \(i-1\) 行及第 \(i\) 行从左到右数前 \(j\) 个格子里面的多米诺骨牌的覆盖情况,其中第 \(i\) 行前 \(j\) 个格子是否可以放置及第 \(i-1\) 行第 \(j+1\sim m\) 这些格子是否可以放置满足 \(sta\) 这个状态的所有方案数。不妨认为 \(sta\) 某一位取 \(0\) 表示这一位未被覆盖,取 \(1\) 表示这一位已被覆盖。
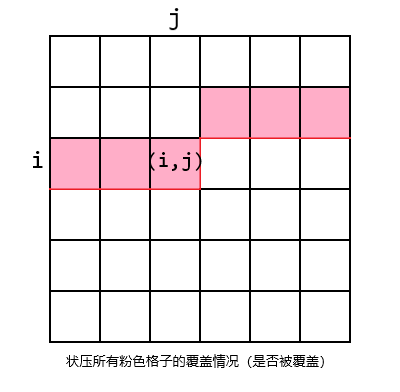
转移的话考虑使用刷表法(用 \(dp(i,j-1,sta)\) 去更新 \(dp(i,j,sta)\) ),如果 \((i,j)\) 这个格子一开始是有障碍物的,那么就不能继续放多米诺骨牌,否则的话如果 \((i,j-1)\) 这个格子在 \(sta\) 中是空的,说明可以在 \((i,j-1),(i,j)\) 这个位置放一个骨牌,如果 \((i-1,j)\) 这个格子在 \(sta\) 中是空的,说明可以在 \((i-1,j),(i,j)\) 这个位置放一个骨牌,按照状态的定义去转移即可。(边界要特殊处理)
接下来考虑以每个格子为障碍物时的答案,可以使用前后缀合并的方法来快速计算答案,先从上往下从左往右做一遍上面说的dp(设求出来的值为 \(up(i,j,sta)\) ),再从下往上从右往左做一遍上面说的dp(设求出来的值为 \(dn(i,j,sta)\) ),设在认为 \((i,j)\) 为障碍物是求出来的dp值为 \(up'()\) 和 \(dn'()\) ,那么 \(up'(i,j-1,sta)=up(i,j-1,sta),dn'(i,j+1,sta)=dn(i,j+1,sta)\) ,根据 \(up'(i,j-1,sta)\) 可以很快求出来 \(up'(i,j,sta)\) ,于是就只需要考虑将 \(up'(i,j,sta)\) 和 \(dn'(i,j+1,sta)\) 这两个状态合并即可,方便起见,认为 \(U(sta)=up'(i,j,sta),D(sta)=dn'(i,j+1,sta)\) 。
枚举 \(sta_0\) 和 \(sta_1\) ,表示上面格子的情况是 \(sta_0\) ,下面格子的情况是 \(sta_1\) ,那么此时 \(sta_0,sta_1\) 对应为空的位置可以选择放或者不放一个多米诺骨牌,设函数 \(\operatorname{bitcnt}(sta)\) 表示二进制数 \(sta\) 的 \(0\) 的数量,那么可以选择放或者不放的位置数量就是 \(\operatorname{bitcnt}(sta_0|sta_1)\) ,所以合并起来得到的答案就是 \(U(sta_0)\times D(sta_1)\times 2^{\operatorname{bitcnt}(sta_0|sta_1)}\) 。
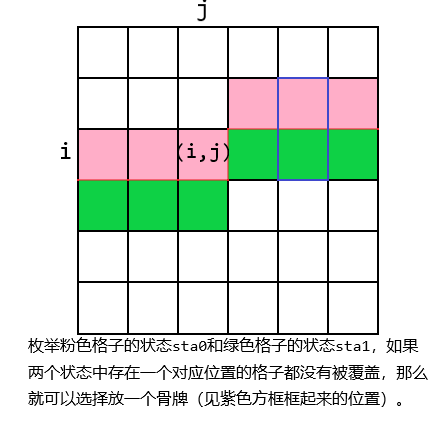
也就是说,这是我们要求的式子:
注意到需要乘以的系数只和 \(sta_0|sta_1\) 有关,所以如果令:
那么答案就是:
使用 FWT 来优化求 \(S(x)\) 的过程,那么总时间复杂度就是 \(\mathcal O(2^nn^3)\) ,不太优美。
考虑不去使用 FWT ,想一想 \(2^{\operatorname{bitcnt}(x)}\) 的意义,可以发现 \(2^{\operatorname{bitcnt}(x)}=\sum_{x\& y=x}1=\sum_{x\in y}1\) ,所以求的式子可以转化为:
(上面这部分的转化也可以理解为枚举 \(s\) 表示拼起来的时候哪些位置会被放上多米诺骨牌)
也就是说只需要求解 \(U()\) 和 \(D()\) 的前缀和就行了,如果暴力求前缀和,总时间复杂度仍然是 \(\mathcal O(2^nn^3)\) ,没有优化,但是需要注意的是,这个求前缀和的过程是可以在状压dp的过程中维护的!
我们可以直接设 \(dp_s(i,j,sta)=\sum_{s\in sta}dp(i,j,s)\) ,然后直接dp求解 \(dp_s(i,j,sta)\) ,考虑状压dp过程中每次转移时修改的位数是很少的,所以可以在每次dp前将需要修改的位置还原成原来的dp值,然后dp完后再将需要修改的位置前缀和回去,这样就可以实现直接维护前缀和了。
这样的总时间复杂度是 \(\mathcal O(2^nn^2)\) ,已经算是很优了。
插头dp
将每个多米诺骨牌视作是两个插头,状态设置和上面讲的类似。
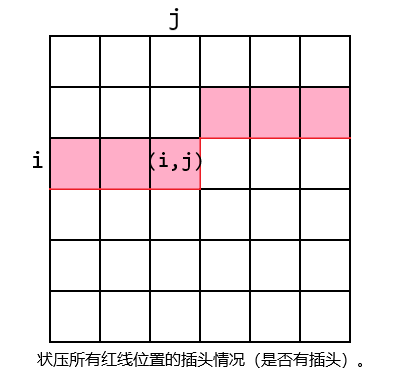
转移的时候还是考虑 \(dp(i-1,j,...)\) 到 \(dp(i,j,...)\) ,如果 \((i,j)\) 为障碍物那么 \((i,j-1)\) 不能有右插头, \((i-1,j)\) 不能有下插头,否则 \((i,j-1)\) 的右插头和 \((i-1,j)\) 的下插头不能同时存在,如果两个存在一个那么这个格子就要和对应格子连起来,如果都不存在就可以不建插头或者新建向下的插头或者新建向右的插头。
求以每个格子为障碍物时的答案还是考虑前后缀合并,由于插头情况已经确定了,所以对于上面的某一个状态下面的状态和它是唯一对应的,所以直接枚举上面的状态找到下面对应的状态即可,时间复杂度为 \(\mathcal O(2^nn^2)\) 。
参考代码
仅提供第一种做法的参考代码。
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define ch() getchar()
#define pc(x) putchar(x)
using namespace std;
template<typename T>void read(T&x){
static char c;static int f;
for(c=ch(),f=1;c<'0'||c>'9';c=ch())if(c=='-')f=-f;
for(x=0;c>='0'&&c<='9';c=ch())x=x*10+(c&15);x*=f;
}
template<typename T>void write(T x){
static char q[65];int cnt=0;
if(x<0)pc('-'),x=-x;
q[++cnt]=x%10,x/=10;
while(x)
q[++cnt]=x%10,x/=10;
while(cnt)pc(q[cnt--]+'0');
}
#define tb(x,t) (((x)>>(t))&1)
#define bt(x,t) ((x)<<(t))
const int maxn=20,upn=17,mod=1000000007;
int mo(const int x){return x>=mod?x-mod:x;}
void add(int&x,int y){x=mo(x+y);}
int up[maxn][maxn][1<<upn],dn[maxn][maxn][1<<upn];
int rev[1<<upn],A[maxn][maxn];
int main(){
int n,m;read(n),read(m);
for(int i=1;i<=n;++i)
for(int j=1;j<=m;++j)
read(A[i][j]);
int U=1<<m;
for(int i=0;i<U;++i)
rev[i]=(rev[i>>1]>>1)|((i&1)<<(m-1));
up[0][m][U-1]=1;
for(int i=1;i<=n;++i){
for(int sta=0;sta<U;++sta)if(tb(sta,0))
add(up[i-1][m][sta],mo(mod-up[i-1][m][sta^bt(1,0)]));
for(int sta=0;sta<U;++sta){
int o=tb(sta,0);
if(!o&&!A[i][1])add(up[i][1][sta^1],up[i-1][m][sta]);
add(up[i][1][sta^o^A[i][1]],up[i-1][m][sta]);
}
for(int sta=0;sta<U;++sta)if(tb(sta,0))
add(up[i][1][sta],up[i][1][sta^bt(1,0)]),
add(up[i-1][m][sta],up[i-1][m][sta^bt(1,0)]);
for(int j=2;j<=m;++j){
for(int sta=0;sta<U;++sta)if(tb(sta,j-2))
add(up[i][j-1][sta],mo(mod-up[i][j-1][sta^bt(1,j-2)]));
for(int sta=0;sta<U;++sta)if(tb(sta,j-1))
add(up[i][j-1][sta],mo(mod-up[i][j-1][sta^bt(1,j-1)]));
for(int sta=0;sta<U;++sta){
int o0=tb(sta,j-2),o1=tb(sta,j-1);
if(!o0&&!A[i][j])add(up[i][j][sta^bt(o0^1,j-2)^bt(o1^1,j-1)],up[i][j-1][sta]);
if(!o1&&!A[i][j])add(up[i][j][sta^bt(o1^1,j-1)],up[i][j-1][sta]);
add(up[i][j][sta^bt(o1^A[i][j],j-1)],up[i][j-1][sta]);
}
for(int sta=0;sta<U;++sta)if(tb(sta,j-2))
add(up[i][j-1][sta],up[i][j-1][sta^bt(1,j-2)]),
add(up[i][j][sta],up[i][j][sta^bt(1,j-2)]);
for(int sta=0;sta<U;++sta)if(tb(sta,j-1))
add(up[i][j-1][sta],up[i][j-1][sta^bt(1,j-1)]),
add(up[i][j][sta],up[i][j][sta^bt(1,j-1)]);
}
}
dn[n+1][1][U-1]=1;
for(int i=n;i>=1;--i){
for(int sta=0;sta<U;++sta)if(tb(sta,0))
add(dn[i+1][1][sta],mo(mod-dn[i+1][1][sta^bt(1,0)]));
for(int sta=0;sta<U;++sta){
int o=tb(sta,0);
if(!o&&!A[i][m])add(dn[i][m][sta^1],dn[i+1][1][sta]);
add(dn[i][m][sta^o^A[i][m]],dn[i+1][1][sta]);
}
for(int sta=0;sta<U;++sta)if(tb(sta,0))
add(dn[i][m][sta],dn[i][m][sta^bt(1,0)]),
add(dn[i+1][1][sta],dn[i+1][1][sta^bt(1,0)]);
for(int j=m-1;j>=1;--j){
for(int sta=0;sta<U;++sta)if(tb(sta,m-j-1))
add(dn[i][j+1][sta],mo(mod-dn[i][j+1][sta^bt(1,m-j-1)]));
for(int sta=0;sta<U;++sta)if(tb(sta,m-j))
add(dn[i][j+1][sta],mo(mod-dn[i][j+1][sta^bt(1,m-j)]));
for(int sta=0;sta<U;++sta){
int o0=tb(sta,m-j-1),o1=tb(sta,m-j);
if(!o0&&!A[i][j])add(dn[i][j][sta^bt(o0^1,m-j-1)^bt(o1^1,m-j)],dn[i][j+1][sta]);
if(!o1&&!A[i][j])add(dn[i][j][sta^bt(o1^1,m-j)],dn[i][j+1][sta]);
add(dn[i][j][sta^bt(o1^A[i][j],m-j)],dn[i][j+1][sta]);
}
for(int sta=0;sta<U;++sta)if(tb(sta,m-j-1))
add(dn[i][j+1][sta],dn[i][j+1][sta^bt(1,m-j-1)]),
add(dn[i][j][sta],dn[i][j][sta^bt(1,m-j-1)]);
for(int sta=0;sta<U;++sta)if(tb(sta,m-j))
add(dn[i][j+1][sta],dn[i][j+1][sta^bt(1,m-j)]),
add(dn[i][j][sta],dn[i][j][sta^bt(1,m-j)]);
}
}
for(int i=1;i<=n;++i){
for(int j=1;j<=m;++j){
if(!A[i][j]){
for(int sta=0;sta<U;++sta)if(tb(sta,j-1)){
up[i][j][sta]=up[i][j][sta^bt(1,j-1)];up[i][j][sta^bt(1,j-1)]=0;
}
int*UP=up[i][j],*DN=(j==m?dn[i+1][1]:dn[i][j+1]);
int ans=0;
for(int sta=0;sta<U;++sta)
ans=mo(ans+1ll*UP[sta]*DN[rev[sta]]%mod);
write(ans);
}
else write(0);
pc(" \n"[j==m]);
}
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号