板刷省选题

目录

板刷省选题

由于各种各样的理由，我开始了板刷省选题的过程。

关于 HNOI

先从 HN 刷起吧，虽然近几年的题目不太可做，但是可以刷些更早的题目。

题单

HNOI2015

亚瑟王

标签

动态规划

难度：easy 。

考察知识点：概率期望 dp 。

关键是分析和设计 dp 状态。

题解

考虑到每张牌最多只会发动一次技能，编号靠前的牌会先考虑是否发动技能并且影响到编号靠后的牌，所以一张牌一张牌地考虑而非一轮一轮地考虑，从后往前考虑而非从前往后考虑。

设 \(f(i,j)\) 表示仅考虑第 \(i\) 张牌及其后面的牌在 \(j\) 轮游戏中造成的期望伤害，转移就是考虑第 \(i\) 张牌是否会在这 \(j\) 轮中的某一轮发动技能，不发动技能的概率是 \((1-p_i)^j\) ，发动的概率是 \([1-(1-p_i)^j]\) ，所以转移就是：

\[f(i,j)=f(i+1,j)\times (1-p_i)^j+(f(i+1,j-1)+d_i)\times [1-(1-p_i)^j] \]

初始值：

\[f(n+1,0\sim r)=f(1\sim n,0)=0 \]

答案就是 \(f(1,r)\) 。

时间复杂度是 \(\mathcal O(Tnr)\) 。

这道题目其实有很多可能会出错的地方，关键还是要想清楚事件与事件之间的相互影响以及 dp 的转移顺序。

一个 trick ：如果前面的决定会影响后面的决定，一般从后往前 dp ；如果后面的决定会影响前面的决定，一般从前往后 dp 。因为这样前面对后面或后面对前面造成的影响就可以比较好地乘在求出来的 dp 值中。

实验比较

标签

动态规划

难度：easy 。

考察知识点：简单组合数学，树形 dp ，二项式反演。

比较套路的一道题目。

考察阅读理解。

题解

不难发现，对于质量相等的图片考虑缩到一个点去考虑，那么题目等价于给定一棵有根森林，要求给每个点标号，需要满足父亲节点标号严格大于儿子节点标号并且标号连续（即如果出现了标号 \(x,y(x<y)\) ，那么 \([x,y]\) 中的所有标号都必须出现过），问标号的方案数。

设 \(f(i)\) 表示不要求标号连续整棵树的标号小于等于 \(i\) 的方案数， \(g(i)\) 表示要求标号连续整棵树的标号小于等于 \(i\) 的方案数，那么就会有：

\[g(n)=\sum_{i=0}^n{n\choose i}f(i) \]

二项式反演可以得到：

\[f(n)=\sum_{i=0}^n(-1)^{n-i}g(i) \]

或者也可以这样做：

\[f(n)=g(n)-\sum_{i=0}^{n-1}{n\choose i}f(i) \]

由此我们就只需要求 \(f(0\sim n)\) 就可以求答案（ \(g(0\sim n)\) ）了，设 \(dp(i,j)\) 表示 \(i\) 标号为 \(j\) 时 \(i\) 这棵子树中所有点标号的方案数，那么转移就是：

\[dp(u,i)=\prod_{v\in \mbox{son}_u}\sum_{j=i+1}dp(v,j) \]

显然可以用前缀和优化。

由于是森林，所以考虑建立虚根 \(n+1\) ，那么 \(f(i)=dp(n+1,i+1)\) 。

时间复杂度 \(\mathcal O(n^2)\) 。

另一种做法是直接设 \(dp(i,j)\) 表示将以 \(i\) 为根的子树分成 \(j\) 种不同标号的方案数，转移就是枚举两棵子树的标号合并成多少种不同的标号，时间复杂度 \(\mathcal O(n^3)\) 。

开店

标签

数据结构

难度： easy 。

考察知识点：点分树，可持久化线段树。

简单数据结构，需要一定的代码实现能力。

题解

可持久化线段树的题解看这里。

点分树做法：对每个分治中心维护不同权值的点到这级分治中心的距离和以及到上一级分治中心的距离和。

接水果

标签

数据结构

难度： easy 。

考察知识点：整体二分， lca 。

简单数据结构，考察了一个套路（判断树上一条路径是否属于另一条路径）。

题解

对于树上的一条路径 \(u-v(\mbox{deep}(u)<\mbox{deep}(v))\) ，如果 \(\mbox{lca}(u,v)\ne u\) ，那么一条路径包含路径 \(u-v\) 当且仅当这条路径的一个端点在 \(u\) 子树内并且另一个端点在 \(v\) 子树内；如果 \(\mbox{lca}(u,v)=u\) ，那么一条路径包含路径 \(u-v\) 当且仅当这条路径的一个端点不在 \(u\) 向 \(v\) 方向走一个节点得到的节点子树内并且另一个端点在 \(v\) 子树内。所以把树拍扁后树上的一条路径对应的就是一个矩形，问题就是询问包含某个点的所有矩形中权值第 \(k\) 大，直接整体二分即可。

菜肴制作

标签

贪心

难度： easy 。

考察知识点：贪心，拓扑排序。

简单贪心。

题解

需要注意的是这道题目字典序比较方式不太一样，这样导致了贪心每次从前面取最小值的做法是错误的，但是如果贪心每次从后面取最大值的做法是正确的，因为后面最大值必然是比其它值要在更后面比较的，所以这样贪心是正确的。

落忆枫音

标签

动态规划

难度： easy 。

考察知识点：DAG 上 dp ，计数，概率期望。

利用概率来计数。

考察阅读理解。

题解

如果没有新增加的边，设每个点入度为 \(d(i)\) ，那么答案就是 \(\prod_{i=1}^nd(i)\) ，相当于是给每个点都分配一个父亲节点，点与点之间是没有影响的。

如果新增加了一条边 \(u\to v\) ，那么给每个点随便分配一个父亲节点就可能会形成一个环，并且这个环必然包含新添加的边，所以这个环会出现当且仅当 \(u\) 选择了 \(v\) 作为父亲节点并且 \(v\) 在 \(u\) 子树内。

设 \(P(i)\) 表示点 \(i\) 在 \(u\) 子树内的概率，那么转移就是 \(P(i)=\sum_{j\to i}P(j)\) ，初始值 \(P(u)=1\) ，答案就是：

\[\prod_{i=1}^nd(i)-P(v)\prod_{i\ne u}d(i) \]

HNOI2016

大数

标签

数据结构

难度： easy 。

考察知识点：分块，莫队，前缀和。

分类讨论。

题解

可以通过后缀和做差的方式提取出 \([l,r]\) 这一段子串组成的数，即 \((S_l-S_{r+1})/10^{n-r}\) ，注意到 \(p\) 是素数，当 \(p\not\mid 10\) 时， \(p\mid (S_l-S_{r+1})/10^{n-r}\Leftrightarrow p\mid (S_l-S_{r+1})\) ，相当于是求区间相等的数对的对数，直接用莫队或者分块做，当 \(p\mid 10\) 时， \(p=2\) 或 \(p=5\) ，此时 \(p\mid x\) 当且仅当 \(x\) 最低位是 \(p\) 的倍数， \([l,r]\) 的答案就是 \(\sum_{i=l}^r[p\mid s_i](i-l+1)=\sum_{i=l}^r[p\mid s_i]i-(l-1)\sum_{i=l}^r[p\mid s_i]\) ，前缀和分别维护两个东西即可。

序列

标签

数据结构

难度： easy 。

考察知识点：单调栈，线段树。

比较套路的数据结构结合应用。

题解

考虑离线，右端点每次往右移动利用单调栈可以较好地维护左端点在某个位置时区间的最小值，用线段树求和就可以很好求出 \(\sum_{j=l}^r\min_{k=j}^ra_k\) ，题目中要求的是 \(\sum_{i=l}^r\sum_{j=l}^i\min_{k=j}^ia_k\) ，可以认为是所有历史值求和，对每个修改除了维护它所改变的值 \(v\) 同时维护它所改变的时间 \(t\) ，设当前时间是 \(T\) ，那么答案应该是 \(\sum_{q}v_q(T-t+1)=(T+1)\sum_qv_q-\sum_qv_qt\) ，同时维护两个东西即可。

上面那种维护历史值求和的方法适用于许多地方，可以当作是一个套路来记。

最小公倍数

标签

数据结构

难度： easy 。

考察知识点：分块，并查集。

比较套路的简单分块题。

题解

暴力一点的想法就是每次询问 \((U,V,A,B)\) 把所有 \(a\le A,b\le B\) 的边 \((u,v,a,b)\) 加入图中，然后看 \(U,V\) 是否连通以及它们所在的连通块中最大的 \(a,b\) 是否等于 \(A,B\) 。

优化暴力的方法就是先将所有边按 \(a\) 排序，然后每隔 \(T\) 分一个块，对于询问的 \((U,V,A,B)\) 中的 \(A\) 在同一个块内的按 \(B\) 大小排序一起处理，用并查集来维护连边，在块内的边先不连，等到处理一个查询的时候再考虑将块内的边给连上去，并且处理完这个查询后就撤销回去，这样的事件复杂度是 \(\mathcal O(\frac{m}{T}m\log_2n+qT\log_2n)\) ，认为 \(n,m,q\) 同阶，当 \(T=\sqrt{n}\) 时时间复杂度是 \(\mathcal O(n\sqrt{n}\log_2n)\) 。

还算是比较常见的一个分块套路：处理双关键字问题时，按某一关键字将修改和查询分块，在同一块内的按另一关键字一起处理。

树

标签

数据结构

难度： easy 。

考察知识点：线段树合并，可持久化线段树， lca 。

需要一点处理技巧的数据结构。

题解

作为学数据结构学傻了的一个可怜娃，我一开始看到这道题目想到的就是可持久化 treap 维护括号序列，然后就自闭了。瞄了一眼题解才发现不是这样的。

维护两棵树，第一棵树是原来的模板树，第二棵树上面的节点表示的是模板树上面的一个子树，这样的话求两个点的 lca 就是第二棵树上面的 lca 对应第一棵树上面的 lca ，能求 lca 就可以很好地求距离了。

矿区

标签

计算几何

难度： normal 。

考察知识点：平面图转对偶图，生成树。

也许是黑科技题目？WC2013考过的平面图转对偶图。

题解

平面图转对偶图，实现方法是将每一条边拆成双向边，然后一条 \(u\to v\) 的边所在的平面中的下一条边就是将 \(v\) 的所有出边极角排序后 \(v\to u\) 这条边的下一条边，算出来的面积是负数的就是无穷域。

以无穷域为根建出生成树，然后一个多边形的某条边如果割掉了一条树边，如果父亲在多边形内部就减去儿子所在子树权值，否则加上儿子所在子树权值，这样求出来得到的结果就恰好是多边形内部所有平面的权值和，然后就很好做的。

需要注意的一个细节就是对偶图可能并不是简单图，会有重边，所以判断一条边是否是树边不能只看父子关系，这里挂了好久。

网络

标签

数据结构

难度： easy 。

考察知识点：二分，线段树，树上路径求交。

这道题目想偏了就可能挽救不回来了。。。错误做法有一点卡空间。

题解

一开始的想法是树上差分树套树然后线段树上面二分，然后空间就被卡爆了。

正解是在线段树上面二分，考虑某一个权值如果不可行当且仅当所有权值大于等于它的所有交互请求的路径都包含这个点，于是可以用线段树来维护一段权值区间的树上路径交，利用 \(\mathcal O(1)\) lca 复杂度就是 \(\mathcal O(n\log_2n)\) 的了。

树上路径求交的方法（从网上看到的）：对于两条相交路径，求出两条路径端点两两 lca 共 4 个点，深度最深的两个点之间的路径就是交，如果路径不相交，用这种方法求出来的两个点必然相等并且存在一条路径没有包含这两个点。

这道题目想到正解很重要的一点就是找到题目中给出的一些特殊限制的性质。（这道题目中就是求的是最大值，如果是第 \(k\) 大树套树就能做而这种做法做不了。）

HNOI2017

单旋

标签

数据结构

难度： easy 。

考察知识点： LCT 。

算是比较水的一道题目了。

题解

不难发现，对于单旋最大值和单旋最小值仅仅是改变很少的一部分连边，直接用 LCT 实现即可，删除也比较简单实现。新插入一个节点这个节点的位置要么就是前驱的右儿子要么就是后继的左儿子，判断一下即可。

可能要注意一下细节。

影魔

标签

数据结构

难度： easy 。

考察知识点： 线段树，树状数组，单调栈。

居然考了和 HNOI2016 序列 很像的一道题目。

考察阅读理解。

题解

一样的移动右端点，用单调递降的单调栈维护，新加入的数字弹掉的所有数以及比这个数字大的第一个数到这个数字这个位置这样的区间的贡献都是 \(p_1\) ，比这个数字大的第一个数到这个数字的位置其它所有地方的贡献都是 \(p_2\) ，除了比它大的第一个数和除它本身外的单调栈中其它地方的位置的贡献都是 \(p_2\) 。（见下图）

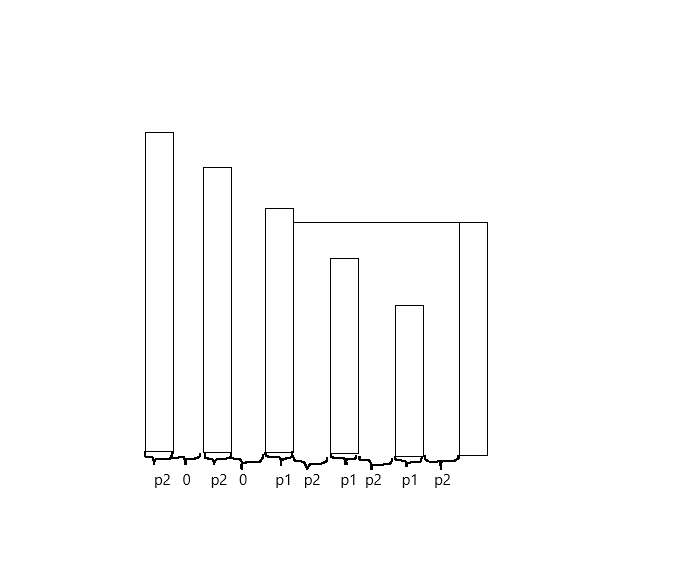
和序列一样的维护方法。

礼物

标签

多项式

难度： easy 。

考察知识点： NTT 、 FFT 。

可能算是多项式板子？？？

题解

话不多说直接推式子：

\[\sum_{i=1}^n(x_i-y_i+c)^2\\ =\sum_{i=1}^n(x_i^2+y_i^2+c^2+2cx_i-2cy_i-2x_iy_i)\\ =nc^2+2c(\sum_{i=1}^nx_i-\sum_{i=1}^ny_i)+\sum_{i=1}^nx_i^2+\sum_{i=1}^ny_i^2-2\sum_{i=1}^nx_iy_i \]

发现唯一变化量就是 \(-2\sum_{i=1}^nx_iy_i\) ，通过卷积就可以很快求出 \(\min(-2\sum_{i=1}^nx_iy_i)\) 。

大佬

标签

假装是数据结构？？？

难度： normal 。

考察知识点：双指针， dp ，hash ， bfs 。

题解

看到题目就知道自己不会写这道题目，于是就借鉴一下你古第一篇题解（ yyb 的题解）的做法。

首先发现可以用来踩大佬的天数是固定的，可以用一个 dp 求出来，设 \(dp(i,j)\) 表示 \(i\) 天中有 \(j\) 天用来刷水题可以获得的最大自信值是多少，那么转移考虑第 \(i\) 天刷不刷水题：

\[dp(i,j)=\max(dp(i-1,j)-a_i,\min(dp(i-1,j-1)-a_i+w_i,\operatorname{mc})) \]

\(\max\) 两边要求可以这个值是合法的。

然后就可以求出最多用多少天踩大佬，预处理出用 \(s\) 天的代价可以得到的所有可能的讽刺能力 \(f(s,i)\) （用 bfs 加 hash 判重），当只怼一次就可以直接判断，当怼两次假设用的天数是 \(d_0,d_1\) ，总天数减 \(2\) 为 \(D\) ，那么两个讽刺能力 \(f(d_0,i),f(d_1,j)\) 的取值需要满足：

\[f(d_0,i)+f(d_1,j)\le C\land f(d_0,i)+f(d_1,j)+D-d_0-d_1\ge C \]

枚举 \(f(d_0,i)\) ，那么满足 \(f(d_0,i)+f(d_1,j)\le C\) 的 \(f(d_1,j)\) 是一段前缀，所以相当于是要找到一段前缀最大的 \(f(d_1,j)-d_1\) 然后判断 \(f(d_0,i)+f(d_1,j)+D-d_0-d_1\) 是否大于等于 \(C\) 即可。

时间复杂度： \(\mathcal O(能过)\) 。

队长快跑

标签

计算几何

难度： easy 。

考察知识点：贪心，凸包，单调队列。

题解

由于保证了只能沿 \(x\) 轴正方向移动并且起点与终点连通，所以每一条射线的方向都可以认为是竖直向上或者竖直向下。（具体证明就算了，还是感性理解吧。）

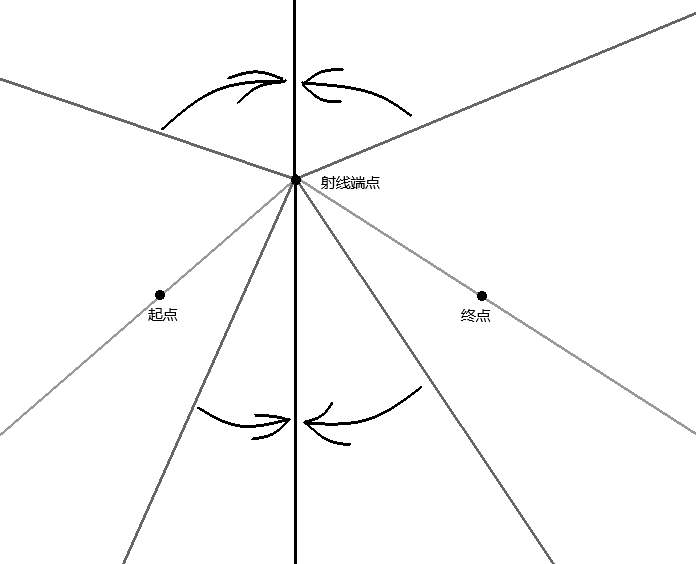
这样处理之后每条射线就只有两种情况，所以维护两个凸包（单调栈），一个是上面的凸包，一个是下面的凸包。

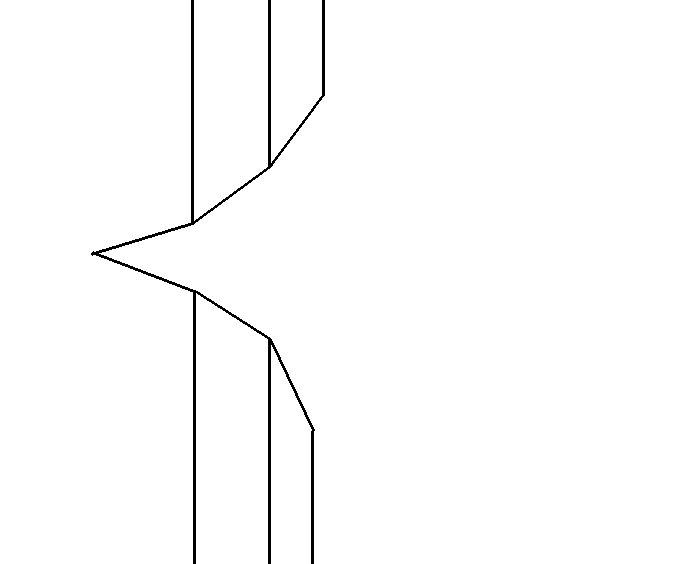
弹栈和普通弹栈一样就行了。

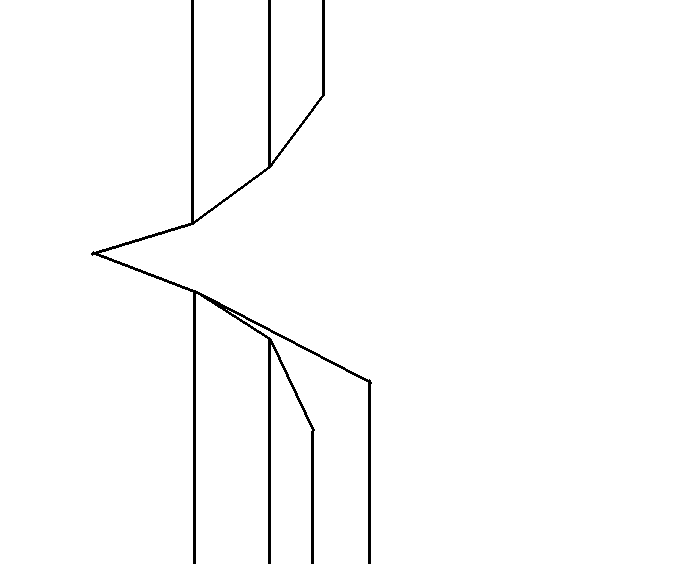
但是将某一个方向的所有点（除起点）都弹掉之后可能会让两个栈之间呈现负角度，此时就需要弹掉另一个栈的栈底（改变起点）同时更新答案直到角度为正为止。

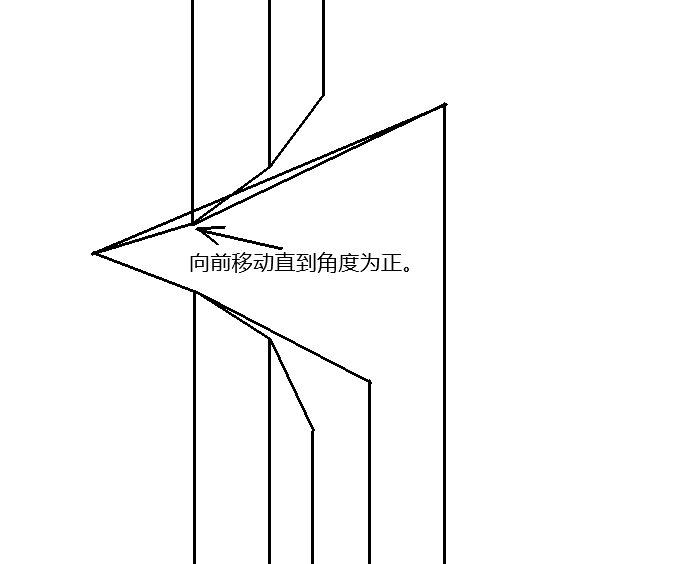
这就是整个算法的关键过程，主要还是要多画图找找感觉。

抛硬币

标签

数论

难度： easy 。

考察知识点：扩展 Lucas ， CRT 。

推式子 + 记算法。

题解

需要注意到的一点是 \(b\le a\le b+10^4\) ，并且还给了一个 \(a=b\) 的部分分，强烈暗示把 \(a\) 拆成 \(b\) ：

\[{a\choose i}=\sum_{j=0}^{a-b}{a-b\choose j}{b\choose i-j} \]

直接推式子：

\[\sum_{i>j}{a\choose i}{b\choose j}\\ =\sum_{i>j}\sum_{t=0}^{a-b}{a-b\choose t}{b\choose i-t}{b\choose j}\\ =\sum_{t=0}^{a-b}{a-b\choose t}\sum_{i>j}{b\choose i-t}{b\choose j}\\ =\sum_{t=0}^{a-b}{a-b\choose t}\sum_{i+t>j}{b\choose i}{b\choose j} \]

设 \(f(t)=\sum_{i+t>j}{b\choose i}{b\choose j}\) ，当 \(0\le t\le a-b\) 时 \(i,j\) 枚举的界限可以不管，则：

\[f(t)=f(t-1)+\sum_{i+t-1=j}{b\choose i}{b\choose j}\\ =f(t-1)+\sum_{i}{b\choose b-i}{b\choose i+t-1}\\ =f(t-1)+{2b\choose b+t-1} \]

\[f(0)=\sum_{i>j}{b\choose i}{b\choose j}\\ =\frac{1}{2}(\sum_{i,j}{b\choose i}{b\choose j}-\sum_{i=j}{b\choose i}{b\choose j})\\ =\frac{1}{2}(2^{2b}-{2b\choose b})\\ 2^{2b-1}-{2b-1\choose b-1} \]

通过扩展 Lucas 我们便可以求出 \(f(0\sim a-b)\) ，答案也就很好算了。

需要注意的是我们需要求的组合数都是一排中相邻的数，所以不必每次都扩展 Lucas ，可以通过上一次求的值加上或减去一些数得到，把扩展 Lucas 稍加扩展即可减少很多常数了。

令 \(T\) 是数据组数，时间复杂度是 \(\mathcal O(T(a-b)\log_2(a-b))\) 。

HNOI2018

寻宝游戏

标签

思维

难度： easy 。

考察知识点： Trie 树，二进制。

分析。

题解

官方题解太神了，先讲讲我自己的做法。

考虑直接硬求，设 \(f(i,S_0,S_1)\) 表示 \(S_0\) 集合位置中的所有数经过前 \(i\) 个数的所有运算后最后是 \(0\) 并且 \(S_1\) 集合位置中的所有数经过前 \(i\) 个运算后最后是 \(1\) 的方案数，那么当 \(S_0=\varnothing\land S_1=\varnothing\) 时，方案数是 \(2^i\) ，当 \(i=0\) 时，方案数是 \([S_1=\varnothing]\) 。

当 \(S_0\ne \varnothing\lor S_1\ne \varnothing\) 时，设第 \(i\) 个数等于 \(0\) 的位置集合为 \(T_0\) ，等于 \(1\) 的位置集合为 \(T_1\) ，那么分情况讨论：当 \(S_0\cap T_1\ne \varnothing\) 时，这个位置填的运算符必须是“与”，当 \(S_1\cap T_0\ne \varnothing\) 时，这个位置填的运算符必须是“或”。如果这个位置可以填“与”，那么 \(f(i,S_0,S_1)\gets f(i,S_0,S_1)+f(i-1,S_0\cap T_1,S_1)\) ；如果这个位置可以填“或”，那么 \(f(i,S_0,S_1)\gets f(i,S_0,S_1)+f(i-1,S_0,S_1\cap T_0)\) 。

事实上并不需要记录 \(f()\) 这个数组的值，可以发现，每一层中我们用到的所有状态都是常数个的，具体证明如下：

求解 \(f(i,S_0,S_1)\) 时，如果这个位置既可以填“与”也可以填“或”，那么 \(S_0\cap T_1=\varnothing\land S_1\cap T_0=\varnothing\) ，此时调用了两个状态分别是 \(f(i-1,\varnothing,S_1),f(i-1,S_0,\varnothing)\) ，如果 \(S_0=\varnothing\) 或者 \(S_1=\varnothing\) ，那么由于至少有一个状态会直接返回答案所以可以认为没有调用，否则调用的两个状态中都至少有一个集合是空集，所以每一层用到的状态是常数个的。

考虑如何表示集合 \(S_0,S_1\) ，如果将所有串依次排列下来并且加上询问串，然后从左往右认为从下往上是一个二进制串并将其插入 Trie 树中，那么我们用到的所有 \(S_0,S_1\) 就都可以用 Trie 树上面的某个节点表示了，但是这样每次询问都需要建 Trie ，复杂度还是假的，考虑到我们实际关心的 Trie 树上面的某个节点只是这个节点表示的集合大小，并且这个集合大小是 dfs 序上一段连续的位置和询问串的交，所以可以通过处理每个询问串 \(0,1\) 个数的前缀和来实现不需要每次询问都建一遍 Trie ，这样时间复杂度就是对的了。

总的时间复杂度是 \(\mathcal O(nm+nq+mq)\) 。

然后讲一下官方题解的神仙做法。

现在有一个数 \(0\) ，然后给定一个 \(01\) 数串和操作串，如何求从左到右依次执行对应位置的操作和数最后得到的结果是多少呢？

把操作串也认为是 \(01\) 串（把“与”认为是 \(1\) ，把“或”认为是 \(0\) ），第一个操作符认为是最高位，那么我们是如何判断某一位最后的结果是 \(0\) 还是 \(1\) 呢？由于“与 \(1\) ”和“或 \(0\) ”对这一位是不会造成影响的，所以我们会从后往前找到第一个操作串和给定的数串不相同的位置，然后数串中这个位置的数就是最后得到的结果，如果数串和操作串完全相同，那么最后得到的结果就是初始值 \(0\) 。

x&1 = x
x|0 = x
0  0101011001
   |&|&|&&||&

从后往前不太好找，将操作串和数串翻转一下，那么其实比较的就是翻转后的操作串和数串的字典序，设操作串和数串翻转后为 \(S\) 和 \(T\) ，那么当 \(T\le S\) 时，结果是 \(0\) ，当 \(T>S\) 时，结果是 \(1\) 。

由此我们便把求结果这个过程转化成了比较字典序大小的问题，而每次询问其实相当于是给操作串 \(T\) 规定了若干个形如 \(T\le S\) 或者 \(T>S\) 的限制，这样就很好求解了。

一开始预处理的排序用 Trie 树或者基数排序，那么时间复杂度就是 \(\mathcal O(nm+mq)\) 。

转盘

标签

数据结构

难度： easy 。

考察知识点：线段树，贪心。

分析和贪心，还考察了用线段树维护单调栈的一个套路。

题解

首先想着去枚举依次标记的物品，但是这样要枚举的东西就太多了，考虑用贪心去减小枚举，如果一个物品被经过了很多次，那么我们只关心最后一次经过它的时间，如果从某个起点开始标记物品，那么这个物品肯定只会经过一次，因为如果经过了两次那么完全可以从这个起点的下一个物品开始选起，而需要的最少时间仍然不变。既然起点不会经过多次，那么必然是到了某一个物品就一直等到它出现然后再去选下一个物品。

如果将起点设置在第 \(x+1\) 这个位置，那么需要的时间就是：

\[\max(\max_{i=1}^x(x-i+T_i),\max_{i=x+1}^n(n+x-i+T_i))=x+\max(\max_{i=1}^x(T_i-i),n+\max_{i=x+1}^n(T_i-i)) \]

设 \(V_i=T_i-i\) ，我们要求的答案就是：

\[\min_{x=0}^{n-1}(x+\max(\max_{i=1}^xV_i,n+\max_{i=x+1}^nV_i)) \]

从这个式子我们可以看出来，当 \(x\) 的选择不会影响到 \(\max(\max_{i=1}^xV_i,n+\max_{i=x+1}^nV_i)\) 时， \(x\) 越小越好，如果将所有数值 \(V_i\) 从左往右丢到单调递减的单调栈中保留下来的下标依次为 \(a_1,a_2,\dots,a_m\) ，那么当 \(x\) 取 \([0,a_1),[a_1,a_2),[a_2,a_3),\dots,[a_{m-1},a_m),[a_{m-1},a_m)\) 这些位置时， \(\max(\max_{i=1}^xV_i,n+\max_{i=x+1}^nV_i)\) 不会受到影响，所以 \(x\) 可能取到的位置就只有 \(0,a_1,a_2,\dots,a_{m-1}\) 。

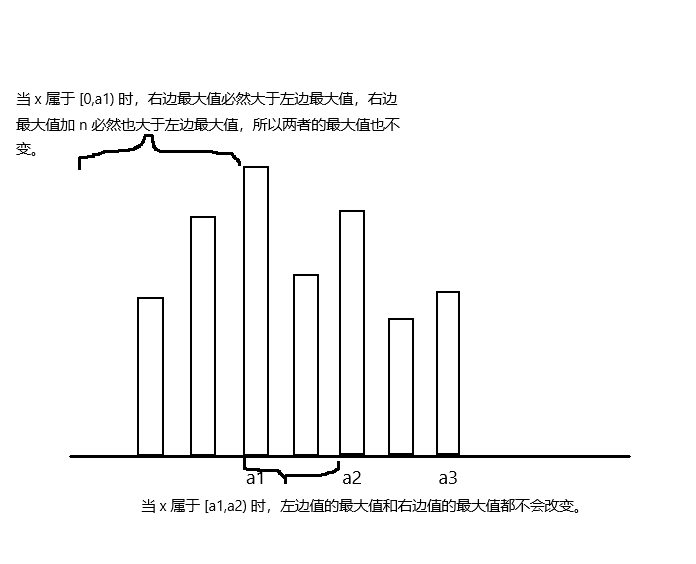
设最大值为 \(S\) ，则 \(S=V_{a_1}\) ，那么当 \(x=0\) 时，答案是 \(n+S\) ，当 \(x=a_p\) 时，答案是 \(a_p+n+\max(S-n,V_{a_{p+1}})\) ，所以我们可以找到满足 \(V_{a_{p+1}}\ge S-n\) 的 \(p\) 所在的区间 \([L,R]\) ，那么这个区间的答案就是 \(a_p+n+V_{a_{p+1}}\) ，用线段树维护单调栈的套路即可求出区间的 \(\min(a_p+n+V_{a_{p+1}})\) ，当 \(p>R\) 时，答案就是 \(a_p+S\) ，肯定希望 \(a_p\) 尽可能地小，所以答案就是 \(a_{R+1}+S\) 。

时间复杂度： \(\mathcal O(n\log_2^2n)\) 。

毒瘤

标签

数据结构

难度： easy 。

考察知识点：动态 dp ，容斥。

感觉难度虚高，我的写法可以用来锻炼码量。

题解

考虑断掉 \(m-n+1\) 条边使得原图变成一棵树，然后要求是若干对点不能都被选，容斥转化成若干对点需要都选，使用动态 dp 来实现要求若干对点都要选的条件。

设 \(dp(u,0/1)\) 表示考虑以 \(u\) 为根的子树，其中 \(u\) 这个点是否选的独立集的方案数，那么转移就是：

\[dp(u,0)=\prod_{u\to v}(dp(v,0)+dp(v,1))\\ dp(u,1)=\prod_{u\to v}dp(v,0) \]

或者考虑将子树 \(v\) 并入 \(u\) ：

\[dp(u,0)\gets dp(u,0)\times (dp(v,0)+dp(v,1))\\ dp(u,1)\gets dp(u,1)\times dp(v,0) \]

写成矩阵形式：

\[\begin{bmatrix}dp(v,0)&\ dp(v,1)\end{bmatrix}\times \begin{bmatrix}dp(u,0)&\ dp(u,1)\\ dp(u,0)&\ 0\end{bmatrix}=\begin{bmatrix}dp(u,0)&\ dp(u,1)\end{bmatrix} \]

然后就可以直接维护了。

需要注意的一点是 dp 值可能会有 \(0\) ，所以需要记录 \(0\) 的个数来实现除以 \(0\) 的操作。

然后还有就是枚举集合的时候，可以使用格雷码来枚举，这样每次只会改一个位置。

时间复杂度 \(\mathcal O(n\log_2n+2^{m-n+1}\log_2n)\) 或 \(\mathcal O(n\log_2n+2^{m-n+1}\log_2^2n)\) 。

游戏

标签

动态规划

难度： easy 。

考察知识点： dp 。

主要考察的是对问题的分析以及寻找问题的性质。

题解

如果一个钥匙在房间 \(x\) ，开的锁在 \(y-y+1\) 之间，那么当 \(x\le y\) 时，右边一定不能跨过 \(y-y+1\) 这扇门，当 \(x>y\) 时，左边一定不能跨过 \(y-y+1\) 这扇门。

由此我们就可以对每个连通块 \(i\) 设一个 \(L_i,R_i\) 分别表示 \(i\) 往左最多能走到哪里、往右最多能走到哪里，然后转移就是一直进行如下操作：如果可以开左边的门，那么令 \(L_i=L_{L_i-1}\) ；如果可以开右边的门，那么令 \(R_i=R_{R_i+1}\) 。复杂度显然是正确的，因为一扇门只会被扩展一次。

排列

标签

贪心

难度： normal 。

考察知识点：贪心，堆。

感觉正解挺难想的，我没有自己想出来，大概还算是很考验思维和分析能力的一道题目吧。

考察阅读理解。

题解

如果令点 \(i\) 的父亲为 \(a_i\) （无解会连出一个环而不是树），那么题目就等价于给每个点不重不漏地标上 \(1\sim n\) 的号，使得一个点标号大于其父亲标号并且最大化标号和权值乘积的和。

把从小到大标号视为是依次选点。先考虑权值最小的点，如果权值最小的点没有父亲肯定直接选权值最小的点，否则的话一选了它父亲一定直接选它自己，也就是这个点一定紧跟着它的父亲选，此时我们就可以把这个点和它父亲合并了。

但是在合并操作之后，每个点代表的可能就是一个序列了，考虑对于一个长度为 \(a\) 的序列 \(\{A\}\) 和一个长度为 \(b\) 的序列 \(\{B\}\) ， \(A\) 放在 \(B\) 前面的代价是 \(\sum_{i=1}^aA_i\times i+\sum_{i=1}^bB_i\times (a+i)\) ， \(B\) 放在 \(A\) 前面的代价是 \(\sum_{i=1}^bB_i\times i+\sum_{i=1}^aA_i\times (b+i)\) ，两个代价的差就是：

\[a\times \sum_{i=1}^bB_i-b\times \sum_{i=1}^aA_i \]

当 \(a\times \sum_{i=1}^bB_i-b\times \sum_{i=1}^aA_i\ge 0\) 即 \((\sum_{i=1}^aA_i)/a\le (\sum_{i=1}^bB_i)/b\) 时， \(A\) 放在 \(B\) 前面更优，所以我们便可以得知两个点（序列）合并的时候得到的点（序列）的权值应该设为所有数的平均数，然后用堆维护最小值和并查集维护合并两个点即可。

道路

标签

动态规划

难度： easy 。

考察知识点： 树形 dp 。

不要想复杂了，想复杂想偏了可能就会想困难了，还有一定要注意到“任意乡村可以通过不超过40条道路到达首都”这个条件。

题解

不要被 \(c_i\cdot (a_i+x)\cdot (b_i+y)\) 迷惑到了，直接设 \(dp(i,j,k)\) 表示考虑以 \(i\) 为根的子树其中从 \(i\) 向上走到根未翻新的公路条数为 \(j\) 铁路条数为 \(k\) 的最小不便利值是多少，那么转移就是（设 \(i\) 的公路儿子为 \(l_i\) ，铁路儿子为 \(r_i\) ）：

\[dp(i,j,k)=\begin{cases}c_i(a_i+j)(b_i+k)&\ i \rm\ is\ a\ leaf\\ \min(dp(l_i,j,k)+dp(r_i,j,k+1),dp(l_i,j+1,k)+dp(r_i,j,k))&\ \rm otherwise\end{cases} \]

HNOI2019

自闭了， HNOI2019 还做个啥啊。

鱼

JOJO

多边形

校园旅行

白兔之舞

序列

参考代码

为了防止这篇文章看起来太短了，所以把 AC 代码加上去。

[HNOI2015]亚瑟王：

#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
using namespace std;
const int maxn=250;
double p[maxn],f[maxn][maxn],sum[maxn][maxn];
int d[maxn];
int main(){
	int test;scanf("%d",&test);
	while(test--){
		int n,r;
		cin>>n>>r;
		for(int i=1;i<=n;++i)
			scanf("%lf %d",&p[i],&d[i]);
		for(int i=1;i<=n;++i){
			sum[i][0]=1.0;
			for(int j=1;j<=r;++j)
				sum[i][j]=sum[i][j-1]*(1.0-p[i]);
		}
		for(int j=1;j<=r;++j)f[n+1][j]=0.0;
		for(int i=n;i>=1;--i){
			for(int j=1;j<=r;++j){
				f[i][j]=f[i+1][j]*sum[i][j]+(f[i+1][j-1]+d[i])*(1.0-sum[i][j]);
			}
		}
		printf("%.100f\n",f[1][r]);
	}
	return 0;
}

[HNOI2015]实验比较：

#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
using namespace std;
template<typename T>void read(T &x){
	x=0;int f(1);char c(getchar());
	for(;!isdigit(c);c=getchar())if(c=='-')f=-f;
	for(; isdigit(c);c=getchar())x=(x<<3)+(x<<1)+(c-'0');
	x*=f;
}
template<typename T>void write(T x){
	if(x<0)putchar('-'),x=-x;
	if(x/10)write(x/10),x%=10;
	putchar(x+'0');
}
const int maxn=105;
const long long mod=1000000007;
int son[maxn],bro[maxn],pa[maxn];
void addson(int u,int v){
	bro[v]=son[u],son[u]=v,pa[v]=u;
}
int fa[maxn];
int ac(int x){
	int tx=x;
	while(x!=fa[x])
		x=fa[x];
	while(tx!=fa[tx]){
		int p=fa[tx];
		fa[tx]=x;tx=p;
	}
	return x;
}
void tog(int x,int y){
	x=ac(x),y=ac(y);
	if(x==y)return;
	fa[x]=y;
}
long long iac[maxn],fac[maxn];
long long binom(int n,int m){
	if(n<m||n<0||m<0)return 0;
	return fac[n]*iac[m]%mod*iac[n-m]%mod;
}
long long mo(long long a){
	return a>=mod?a-mod:a;
}
long long dp[maxn][maxn],tmp[maxn];
int sz[maxn];
void solve(int u){
	sz[u]=1;dp[u][0]=1;
	for(int v=son[u];v;v=bro[v]){
		solve(v);
		for(int k=0;k<sz[u]+sz[v];++k)
			tmp[k]=0;
		for(int i=0;i<sz[u];++i){
			for(int j=1;j<=sz[v];++j){
				for(int k=max(i,j);k<=i+j;++k){
					tmp[k]=mo(tmp[k]+dp[u][i]*dp[v][j-1]%mod*binom(k,i)%mod*binom(i,i+j-k)%mod);
				}
			}
		}
		sz[u]+=sz[v];
		for(int i=0;i<sz[u];++i)
			dp[u][i]=tmp[i];
	}
}
int fro[maxn],to[maxn];
int main(){
	int n,m;
	read(n),read(m);
	for(int i=1;i<=n;++i)
		fa[i]=i;
	iac[0]=iac[1]=1;
	for(int i=2;i<=n;++i)
		iac[i]=(mod-mod/i)*iac[mod%i]%mod;
	fac[0]=fac[1]=1;
	for(int i=2;i<=n;++i)
		iac[i]=iac[i]*iac[i-1]%mod,fac[i]=fac[i-1]*i%mod;
	int cnt=0;
	while(m--){
		int u,v;
		read(u);
		char c=getchar();
		while(c!='<'&&c!='=')
			c=getchar();
		read(v);
		if(c=='=')tog(u,v);
		else fro[cnt]=u,to[cnt]=v,++cnt;
	}
	while(cnt--)
		addson(ac(fro[cnt]),ac(to[cnt]));
	for(int i=1;i<=n;++i){
		if(ac(i)!=i)continue;
		if(!pa[i])addson(n+1,i);
	}
	solve(n+1);
	long long ans=0;
	for(int i=1;i<=sz[n+1];++i)
		ans=mo(ans+dp[n+1][i]);
	write(ans);
	return 0;
}

[HNOI2015]开店：

#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
#define ll long long
using namespace std;
template<typename T>void read(T &x){
	x=0;int f(1);char c(getchar());
	for(;!isdigit(c);c=getchar())if(c=='-')f=-f;
	for(; isdigit(c);c=getchar())x=(x<<3)+(x<<1)+(c-'0');
	x*=f;
}
template<typename T>void write(T x){
	if(x<0)putchar('-'),x=-x;
	if(x/10)write(x/10),x%=10;
	putchar(x+'0');
}
const int maxn=160005,saxn=30000007;
ll sm[maxn],smd[maxn],dis[maxn],SUM[saxn];
int LS[saxn],RS[saxn],TIMES[saxn];
int points;
int change(int pre,int l,int r,int L,int R){
	int rt=++points;
	LS[rt]=LS[pre],RS[rt]=RS[pre];
	SUM[rt]=SUM[pre],TIMES[rt]=TIMES[pre];
	if(L<=l&&r<=R)return ++TIMES[rt],rt;
	SUM[rt]+=sm[min(r,R)]-sm[max(l,L)-1];int mid=(l+r)>>1;
	if(R>mid)RS[rt]=change(RS[rt],mid+1,r,L,R);
	if(L<=mid)LS[rt]=change(LS[rt],l,mid,L,R);
	return rt;
}
ll query(int rt,int l,int r,int L,int R){
	ll re=TIMES[rt]*(sm[min(r,R)]-sm[max(l,L)-1]);
	if(L<=l&&r<=R)return re+=SUM[rt];
	int mid=(l+r)>>1;
	if(R>mid)re+=query(RS[rt],mid+1,r,L,R);
	if(L<=mid)re+=query(LS[rt],l,mid,L,R);
	return re;
}
struct Edge{
	int v,w,nt;
	Edge(int v=0,int w=0,int nt=0):v(v),w(w),nt(nt){}
}e[maxn*2];
int hd[maxn],num;
void add_edge(int u,int v,int w){
	e[++num]=Edge(v,w,hd[u]);hd[u]=num;
}
void add(int u,int v,int w){
	add_edge(u,v,w);add_edge(v,u,w);
}
int sz[maxn],sxn[maxn],pa[maxn];
void dfs1(int u){
	int mx=0;sz[u]=1;
	for(int i=hd[u];i;i=e[i].nt){
		int v=e[i].v;
		if(v==pa[u])continue;
		pa[v]=u;dis[v]=dis[u]+e[i].w;
		dfs1(v);sz[u]+=sz[v];
		if(sz[v]>mx)mx=sz[v],sxn[u]=v;
	}
}
int cnt,dfn[maxn],top[maxn];
void dfs2(int u){
	dfn[u]=++cnt;
	if(!sxn[u])return;
	top[sxn[u]]=top[u];dfs2(sxn[u]);
	for(int i=hd[u];i;i=e[i].nt){
		int v=e[i].v;
		if(v==pa[u])continue;
		if(v!=sxn[u]){
			top[v]=v;
			dfs2(v);
		}
		sm[dfn[v]]=e[i].w;
	}
}
int rt,root[maxn];
struct FUCK{
	int id,age;
	FUCK(int id=0,int age=0):id(id),age(age){}
	bool operator < (const FUCK o)const{
		return age==o.age?id<o.id:age<o.age;
	}
}fuck[maxn];
void prepare(int x){
	int cp=x;x=fuck[x].id;
	while(x){
		rt=change(rt,1,cnt,dfn[top[x]],dfn[x]);
		x=pa[top[x]];
	}
	root[cp]=rt;
}
ll eraperp(int Rt,int x){
	ll re=0;
	while(x){
		re+=query(Rt,1,cnt,dfn[top[x]],dfn[x]);
		x=pa[top[x]];
	}
	return re;
}
int main(){
	int n,Q,A;
	read(n),read(Q),read(A);
	for(int i=1;i<=n;++i)
		read(fuck[i].age),fuck[i].id=i;
	sort(fuck+1,fuck+n+1);
	for(int i=2;i<=n;++i){
		int u,v,w;
		read(u),read(v),read(w);
		add(u,v,w);
	}
	dfs1(1);top[1]=1;dfs2(1);
	for(int i=1;i<=n;++i){
		sm[i]+=sm[i-1];
		smd[i]=smd[i-1]+dis[fuck[i].id];
	}
	for(int i=1;i<=n;++i)
		prepare(i);
	ll ans=0;
	while(Q--){
		int u,l,r;
		read(u),read(l),read(r);
		l=(l+ans)%A;r=(r+ans)%A;
		if(l>r)swap(l,r);
		l=lower_bound(fuck+1,fuck+n+1,FUCK(0,l))-fuck;
		r=upper_bound(fuck+1,fuck+n+1,FUCK(0x3f3f3f3f,r))-fuck-1;
		ans=dis[u]*(r-l+1)+smd[r]-smd[l-1]-(eraperp(root[r],u)-eraperp(root[l-1],u))*2;
		write(ans);putchar('\n');
	}
	return 0;
}

[HNOI2015]接水果：

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define ch() getchar()
#define pc(x) putchar(x)
using namespace std;
template<typename T>void read(T&x){
	static char c;static int f;
	for(c=ch(),f=1;c<'0'||c>'9';c=ch())if(c=='-')f=-f;
	for(x=0;c>='0'&&c<='9';c=ch())x=x*10+(c&15);x*=f;
}
template<typename T>void write(T x){
	static char q[65];int cnt=0;
	if(x<0)pc('-'),x=-x;
	q[++cnt]=x%10,x/=10;
	while(x)
		q[++cnt]=x%10,x/=10;
	while(cnt)pc(q[cnt--]+'0');
}
const int maxn=40005,maxp=40005,maxq=40005;
int n;
int tr[maxn];
void change(int pos,int val){
	while(pos<=n){
		tr[pos]+=val;
		pos+=pos&(-pos);
	}
}
int query(int pos){
	int re=0;
	while(pos){
		re+=tr[pos];
		pos^=pos&(-pos);
	}
	return re;
}
void change(int l,int r,int val){
	change(l,val);change(r+1,-val);
}
struct Edge{
	int v,nt;
	Edge(int v=0,int nt=0):
		v(v),nt(nt){}
}e[maxn*2];
int hd[maxn],num;
void qwq(int u,int v){
	e[++num]=Edge(v,hd[u]),hd[u]=num;
}
int dfn[maxn],sz[maxn],pa[maxn][18],cnt,deep[maxn];
void dfs(int u,int fa,int dp){
	deep[u]=dp;dfn[u]=++cnt;
	sz[u]=1;pa[u][0]=fa;
	for(int i=1;(1<<i)<=dp;++i)
		pa[u][i]=pa[pa[u][i-1]][i-1];
	for(int i=hd[u];i;i=e[i].nt){
		int v=e[i].v;
		if(v==fa)continue;
		dfs(v,u,dp+1);sz[u]+=sz[v];
	}
}
struct Matrix{
	int l0,r0,l1,r1,val;
	Matrix(int l0=0,int r0=0,int l1=0,int r1=0,int val=0):
		l0(l0),r0(r0),l1(l1),r1(r1),val(val){}
}S[maxp*2],SL[maxp*2],SR[maxp*2];
int W[maxp],cw;
struct Query{
	int x,y,k,id;
	Query(int x=0,int y=0,int k=0,int id=0):
		x(x),y(y),k(k),id(id){}
}Q[maxq],QL[maxq],QR[maxq];
struct Line{
	int l,r,h,v;
	Line(int l=0,int r=0,int h=0,int v=0):
		l(l),r(r),h(h),v(v){}
	bool operator < (const Line o)const{
		return h^o.h?h<o.h:l^o.l?l<o.l:r^o.r?r<o.r:v<o.v;
	}
}Ls[maxp*4+maxq*2];
int Ans[maxq];
void solve(int l,int r,int L,int R,int ql,int qr){
	if(ql>qr)return;
	int mid=(l+r)>>1;
	if(l==r){
		for(int i=ql;i<=qr;++i)
			Ans[Q[i].id]=W[mid-1];
		return;
	}
	int cnt=0;
	int csl=0,csr=0;
	for(int i=L;i<=R;++i){
		if(S[i].val<=mid){
			Ls[++cnt]=Line(S[i].l0,S[i].r0,S[i].l1,1);
			Ls[++cnt]=Line(S[i].l0,S[i].r0,S[i].r1+1,-1);
			SL[++csl]=S[i];
		}
		else
			SR[++csr]=S[i];
	}
	for(int i=ql;i<=qr;++i){
		Ans[Q[i].id]=0;
		Ls[++cnt]=Line(n+1,Q[i].x,Q[i].y,Q[i].id);
		Ls[++cnt]=Line(n+1,Q[i].y,Q[i].x,Q[i].id);
	}
	sort(Ls+1,Ls+cnt+1);
	for(int i=1;i<=cnt;++i){
		if(Ls[i].l==n+1)
			Ans[Ls[i].v]+=query(Ls[i].r);
		else
			change(Ls[i].l,Ls[i].r,Ls[i].v);
	}
	int cql=0,cqr=0;
	for(int i=ql;i<=qr;++i){
		if(Ans[Q[i].id]>=Q[i].k)
			QL[++cql]=Q[i];
		else
			QR[++cqr]=Q[i],
			QR[cqr].k-=Ans[Q[i].id];
	}
	for(int i=1;i<=csl;++i)S[L+i-1]=SL[i];
	for(int i=1;i<=csr;++i)S[L+csl+i-1]=SR[i];
	for(int i=1;i<=cql;++i)Q[ql+i-1]=QL[i];
	for(int i=1;i<=cqr;++i)Q[ql+cql+i-1]=QR[i];
	solve(l,mid,L,L+csl-1,ql,ql+cql-1);
	solve(mid+1,r,L+csl,R,ql+cql,qr);
}
int main(){
	int p,q;
	read(n),read(p),read(q);
	for(int i=1;i<n;++i){
		int u,v;
		read(u),read(v);
		qwq(u,v);qwq(v,u);
	}
	dfs(1,0,0);
	int cp=0;
	for(int i=1;i<=p;++i){
		int u,v,w;
		read(u),read(v),read(w);W[cw++]=w;
		if(deep[u]<deep[v])u^=v^=u^=v;int cu=u;
		if(deep[u]!=deep[v])for(int t=deep[u]-deep[v]-1,cn=0;t;t>>=1,++cn)
			if(t&1)cu=pa[cu][cn];
		if(pa[cu][0]==v){
			if(dfn[cu]-1>=1)S[++cp]=Matrix(1,dfn[cu]-1,dfn[u],dfn[u]+sz[u]-1,w);
			if(dfn[cu]+sz[cu]<=n)S[++cp]=Matrix(dfn[cu]+sz[cu],n,dfn[u],dfn[u]+sz[u]-1,w);
		}
		else
			S[++cp]=Matrix(dfn[u],dfn[u]+sz[u]-1,dfn[v],dfn[v]+sz[v]-1,w);
	}
	sort(W,W+cw);cw=unique(W,W+cw)-W;
	for(int i=1;i<=cp;++i){
		S[i].val=lower_bound(W,W+cw,S[i].val)-W+1;
	}
	for(int i=1;i<=q;++i){
		int u,v,k;
		read(u),read(v),read(k);
		Q[i]=Query(dfn[u],dfn[v],k,i);
	}
	solve(1,cw,1,cp,1,q);
	for(int i=1;i<=q;++i)
		write(Ans[i]),pc('\n');
	return 0;
}

[HNOI2015]菜肴制作：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
template<typename T>inline void read(T &x){
	x=0;int f(1);char c(getchar());
	for(;!isdigit(c);c=getchar())if(c=='-')f=-f;
	for(; isdigit(c);c=getchar())x=(x<<3)+(x<<1)+(c-'0');
	x*=f;
}
template<typename T>inline void write(T x){
	if(x<0)putchar('-'),x=-x;
	if(x/10)write(x/10),x%=10;
	putchar(x+'0');
}
const int maxn=100005,maxm=100005;
struct priority_queue{
	int a[maxn],num;
	inline void push(int x){
		int now=++num;
		a[now]=x;
		while(now>1&&a[now/2]<a[now])
			swap(a[now/2],a[now]),now/=2;
	}
	inline void pop(void){
		int now=1;swap(a[now],a[num--]);
		while(1){
			int nt=now;
			if(now*2<=num&&a[now*2]>a[nt])nt=now*2;
			if(now*2+1<=num&&a[now*2+1]>a[nt])nt=now*2+1;
			if(nt==now)break;
			swap(a[nt],a[now]);now=nt;
		}
	}
	inline int top(void){
		return a[1];
	}
	inline int size(void){
		return num;
	}
}q;
struct Edge{
	int v,nt;
}edge[maxm];
int hd[maxn],num;
inline void add_edge(int u,int v){
	++num,edge[num].v=v,edge[num].nt=hd[u],hd[u]=num;
}
int ans[maxn],vis[maxn];
int main(){
	int T;read(T);
	while(T--){
		memset(vis,0,sizeof vis);
		memset(hd,0,sizeof hd);
		num=0;int n,m;read(n),read(m);
		for(register int i=1,u,v;i<=m;++i){
			read(u),read(v);add_edge(v,u);++vis[u];
		}
		for(register int i=1;i<=n;++i)
			if(!vis[i])
				q.push(i);
		int cnt=0;
		while(q.size()){
			int x=q.top();q.pop();
			ans[cnt++]=x;
			for(int i=hd[x];i;i=edge[i].nt){
				int v=edge[i].v;--vis[v];
				if(!vis[v])q.push(v);
			}
		}
		if(cnt==n){while(cnt--)write(ans[cnt]),putchar(' ');putchar('\n');}
		else puts("Impossible!");
	}
	return 0;
}

[HNOI2015]落忆枫音：

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define ch() getchar()
#define pc(x) putchar(x)
using namespace std;
template<typename T>void read(T&x){
	static char c;static int f;
	for(c=ch(),f=1;c<'0'||c>'9';c=ch())if(c=='-')f=-f;
	for(x=0;c>='0'&&c<='9';c=ch())x=x*10+(c&15);x*=f;
}
template<typename T>void write(T x){
	static char q[65];int cnt=0;
	if(x<0)pc('-'),x=-x;
	q[++cnt]=x%10,x/=10;
	while(x)
		q[++cnt]=x%10,x/=10;
	while(cnt)pc(q[cnt--]+'0');
}
const int mod=1000000007;
int mo(const int x){
	return x>=mod?x-mod:x;
}
const int maxn=100005,maxm=200005;
struct Edge{
	int v,nt;
	Edge(int v=0,int nt=0):
		v(v),nt(nt){}
}e[maxm];
int hd[maxn],num;
void qwq(int u,int v){
	e[++num]=Edge(v,hd[u]),hd[u]=num;
}
int d[maxn],inv[maxn],q[maxn],P[maxn];
int main(){
	int n,m,x,y;
	read(n),read(m),read(x),read(y);
	inv[1]=1;
	for(int i=2;i<=n;++i)
		inv[i]=1ll*(mod-mod/i)*inv[mod%i]%mod;
	while(m--){
		int u,v;
		read(u),read(v);
		qwq(v,u);++d[u];
	}
	int fro=0,bac=0;
	for(int i=1;i<=n;++i)
		if(!d[i])q[bac++]=i;
	while(fro<bac){
		int u=q[fro++];
		for(int i=hd[u];i;i=e[i].nt){
			int v=e[i].v;
			if((--d[v])==0)
				q[bac++]=v;
		}
	}
	int tmp0=1,tmp1=1;
	for(int i=n-2;~i;--i){
		int u=q[i],cnt=0;
		for(int j=hd[u];j;j=e[j].nt){
			++cnt;int v=e[j].v;
			P[u]=mo(P[u]+P[v]);
		}
		P[u]=1ll*P[u]*inv[cnt]%mod;
		if(u==y)
			P[u]=1,++cnt;
		else
			tmp1=1ll*tmp1*cnt%mod;
		tmp0=1ll*tmp0*cnt%mod;
	}
	write(mo(mod-1ll*P[x]*tmp1%mod+tmp0));pc('\n');
	return 0;
}

[HNOI2016]大数：

#include<cmath>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define ch() getchar()
#define pc(x) putchar(x)
using namespace std;
template<typename T>void read(T&x){
	static char c;static int f;
	for(c=ch(),f=1;c<'0'||c>'9';c=ch())if(c=='-')f=-f;
	for(x=0;c>='0'&&c<='9';c=ch())x=x*10+(c&15);x*=f;
}
template<typename T>void write(T x){
	static char q[65];int cnt=0;
	if(x<0)pc('-'),x=-x;
	q[++cnt]=x%10,x/=10;
	while(x)
		q[++cnt]=x%10,x/=10;
	while(cnt)pc(q[cnt--]+'0');
}
const int maxn=200005,maxq=200005;
char s[maxn];
int sum[maxn],qwq[maxn];
int cnt[maxn],I[maxn];
long long ans;
struct Query{
	int l,r,id;
	Query(int l=0,int r=0,int id=0):
		l(l),r(r),id(id){}
	bool operator < (const Query o)const{
		return I[l]^I[o.l]?I[l]<I[o.l]:(I[l]&1)?r<o.r:r>o.r;
	}
}Q[maxq];
long long Ans[maxq];
int tr0[maxn];long long tr1[maxn];
int main(){
	int n,p;read(p);
	scanf("%s",s+1);
	n=strlen(s+1);
	if(p!=2&&p!=5){
		int cn=0;qwq[cn++]=0;s[0]='0';
		for(int i=n,tmp=1;i>=1;--i,tmp=1ll*tmp*10%p)
			qwq[cn++]=sum[i]=(sum[i+1]+1ll*tmp*(s[i]-'0')%p)%p;++n;
		sort(qwq,qwq+cn);cn=unique(qwq,qwq+cn)-qwq;int sqr=sqrt(n);
		for(int i=1;i<=n;++i)
			sum[i]=lower_bound(qwq,qwq+cn,sum[i])-qwq+1,
			I[i]=I[i-1]+((i-1)%sqr==0);
		I[n+1]=I[n]+1;
		int q;read(q);
		for(int i=1;i<=q;++i){
			read(Q[i].l);read(Q[i].r);++Q[i].r;Q[i].id=i;
		}
		sort(Q+1,Q+q+1);
		for(int i=1,nl=1,nr=0;i<=q;++i){
			while(nl>Q[i].l)ans+=(cnt[sum[--nl]]++);
			while(nr<Q[i].r)ans+=(cnt[sum[++nr]]++);
			while(nl<Q[i].l)ans-=(--cnt[sum[nl++]]);
			while(nr>Q[i].r)ans-=(--cnt[sum[nr--]]);
			Ans[Q[i].id]=ans;
		}
		for(int i=1;i<=q;++i)
			write(Ans[i]),pc('\n');
	}
	else{
		for(int i=1;i<=n;++i){
			int o=((s[i]-'0')%p==0);
			tr0[i]=tr0[i-1]+o;
			tr1[i]=tr1[i-1]+o*i;
		}
		int q;read(q);
		while(q--){
			int l,r;read(l),read(r);
			int tmp0=tr0[r]-tr0[l-1];
			long long tmp1=tr1[r]-tr1[l-1];
			write(tmp1-1ll*tmp0*(l-1)),pc('\n');
		}
	}
	return 0;
}

[HNOI2016]序列

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define ch() getchar()
#define pc(x) putchar(x)
using namespace std;
template<typename T>void read(T&x){
	static char c;static int f;
	for(c=ch(),f=1;c<'0'||c>'9';c=ch())if(c=='-')f=-f;
	for(x=0;c>='0'&&c<='9';c=ch())x=x*10+(c&15);x*=f;
}
template<typename T>void write(T x){
	static char q[65];int cnt=0;
	if(x<0)pc('-'),x=-x;
	q[++cnt]=x%10,x/=10;
	while(x)
		q[++cnt]=x%10,x/=10;
	while(cnt)pc(q[cnt--]+'0');
}
const int maxn=100005,maxq=100005;
int n;
struct Tree{
	long long tag[maxn<<2],sum[maxn<<2];
	int len[maxn<<2];
	void build(int x,int l,int r){
		len[x]=r-l+1;tag[x]=sum[x]=0;
		if(l==r)return;int mid=(l+r)>>1;
		build(x<<1,l,mid);build(x<<1|1,mid+1,r);
	}
	void push(int x,long long v){
		tag[x]+=v;sum[x]+=v*len[x];
	}
	void pushup(int x){
		sum[x]=sum[x<<1]+sum[x<<1|1];
	}
	void pushdown(int x){
		if(tag[x]==0)return;
		push(x<<1,tag[x]);
		push(x<<1|1,tag[x]);
		tag[x]=0;
	}
	void change(int x,int l,int r,int L,int R,long long v){
		if(L<=l&&r<=R)return push(x,v);
		pushdown(x);int mid=(l+r)>>1;
		if(L<=mid)change(x<<1,l,mid,L,R,v);
		if(R>mid)change(x<<1|1,mid+1,r,L,R,v);
		return pushup(x);
	}
	long long query(int x,int l,int r,int L,int R){
		if(L<=l&&r<=R)return sum[x];
		pushdown(x);int mid=(l+r)>>1;long long re=0;
		if(L<=mid)re+=query(x<<1,l,mid,L,R);
		if(R>mid)re+=query(x<<1|1,mid+1,r,L,R);
		return re;
	}
}T0,T1,T2;
struct Edge{
	int v,w,nt;
	Edge(int v=0,int w=0,int nt=0):
		v(v),w(w),nt(nt){}
}e[maxq];
int hd[maxn],num;
void qwq(int u,int v,int w){
	e[++num]=Edge(v,w,hd[u]),hd[u]=num;
}
int a[maxn],st[maxn],tim[maxn];
long long Ans[maxn];
int main(){
	int q;read(n),read(q);
	for(int i=1;i<=n;++i)read(a[i]);
	for(int i=1;i<=q;++i){
		int l,r;
		read(l),read(r);
		qwq(r,l,i);
	}
	T0.build(1,1,n);
	T1.build(1,1,n);
	T2.build(1,1,n);
	int tp=0;
	for(int i=1;i<=n;++i){
		while(tp&&a[st[tp]]>a[i]){
			T0.change(1,1,n,st[tp-1]+1,st[tp],1ll*(i-st[tp])*a[st[tp]]);
			T1.change(1,1,n,st[tp-1]+1,st[tp],-a[st[tp]]);
			T2.change(1,1,n,st[tp-1]+1,st[tp],-1ll*st[tp]*a[st[tp]]);
			--tp;
		}
		st[++tp]=i;
		T1.change(1,1,n,st[tp-1]+1,i,a[i]);
		T2.change(1,1,n,st[tp-1]+1,i,1ll*i*a[i]);
		for(int j=hd[i];j;j=e[j].nt)
			Ans[e[j].w]=T0.query(1,1,n,e[j].v,i)+(T1.query(1,1,n,e[j].v,i)*(i+1)-T2.query(1,1,n,e[j].v,i));
	}
	for(int i=1;i<=q;++i)
		write(Ans[i]),pc('\n');
	return 0;
}

[HNOI2016]最小公倍数：

#include<cmath>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#include<assert.h>
#define ch() getchar()
#define pc(x) putchar(x)
using namespace std;
template<typename T>void read(T&x){
	static char c;static int f;
	for(c=ch(),f=1;c<'0'||c>'9';c=ch())if(c=='-')f=-f;
	for(x=0;c>='0'&&c<='9';c=ch())x=x*10+(c&15);x*=f;
}
template<typename T>void write(T x){
	static char q[65];int cnt=0;
	if(x<0)pc('-'),x=-x;
	q[++cnt]=x%10,x/=10;
	while(x)
		q[++cnt]=x%10,x/=10;
	while(cnt)pc(q[cnt--]+'0');
}
const int maxn=50005,maxm=100005,maxq=50005;
struct Edge{
	int u,v,a,b;
	Edge(int u=0,int v=0,int a=0,int b=0):
		u(u),v(v),a(a),b(b){}
}e[maxm],te[maxm];
bool cmpa(const Edge A,const Edge B){
	return A.a^B.a?A.a<B.a:A.b^B.b?A.b<B.b:A.u^B.u?A.u<B.u:A.v<B.v;
}
bool cmpb(const Edge A,const Edge B){
	return A.b^B.b?A.b<B.b:A.a^B.a?A.a<B.a:A.u^B.u?A.u<B.u:A.v<B.v;
}
int pa[maxn],sz[maxn],mx2[maxn],mx3[maxn];
int st[maxm],tp,cv2[maxm],cv3[maxm];
int Ac(int x){
	while(pa[x]!=x)
		x=pa[x];
	return x;
}
void Merge(int x,int y,int _2,int _3){
	++tp;
	if((x=Ac(x))!=(y=Ac(y))){
		if(sz[x]>sz[y])x^=y^=x^=y;
		pa[x]=y;sz[y]+=sz[x];
		_2=max(_2,mx2[x]);_3=max(_3,mx3[x]);
	}
	st[tp]=x;
	cv2[tp]=mx2[y];cv3[tp]=mx3[y];
	mx2[y]=max(mx2[y],_2);
	mx3[y]=max(mx3[y],_3);
}
void IN(Edge tmp){
	Merge(tmp.u,tmp.v,tmp.a,tmp.b);
}
void OUT(void){
	int x=st[tp],y=pa[x];
	if(y!=x){
		mx2[y]=cv2[tp],mx3[y]=cv3[tp];
		sz[y]-=sz[x];pa[x]=x;
	}
	else
		mx2[x]=cv2[tp],mx3[x]=cv3[tp];
	--tp;
}
int I[maxm];
struct Query{
	int u,v,a,b,id;
	Query(int u=0,int v=0,int a=0,int b=0,int id=0):
		u(u),v(v),a(a),b(b),id(id){}
	bool operator < (const Query o)const{
		return I[a]^I[o.a]?I[a]<I[o.a]:b<o.b;
	}
}Q[maxq];
int n;
void init(void){
	tp=0;
	for(int i=1;i<=n;++i)
		sz[pa[i]=i]=1,
		mx2[i]=mx3[i]=-1;
}
int Ans[maxq];
int RM[1005],LM[1005];
int main(){
	int m;read(n),read(m);
	for(int i=1;i<=m;++i){
		int u,v,a,b;
		read(u),read(v),read(a),read(b);
		e[i]=Edge(u,v,a,b);
	}
	sort(e+1,e+m+1,cmpa);
	for(int i=1;i<=m;++i)
		te[i]=Edge(e[i].u,e[i].v,i,e[i].b);
	sort(te+1,te+m+1,cmpb);
	int sqr=sqrt(m);
	for(int i=1;i<=m;++i){
		if((i-1)%sqr==0)
			I[i]=I[i-1]+1,
			LM[I[i]]=i;
		else
			I[i]=I[i-1];
		RM[I[i]]=i;
	}
	I[m+1]=I[m]+1;
	int q;read(q);
	for(int i=1;i<=q;++i){
		int u,v,a,b;
		read(u),read(v),read(a),read(b);
		int l=1,r=m;
		while(l<r){
			int mid=(l+r+1)>>1;
			if(e[mid].a<=a)l=mid;
			else r=mid-1;
		}
		Q[i]=Query(u,v,l=r,b,i);
	}
	sort(Q+1,Q+q+1);init();
	for(int i=1,tot=0,dn=0;i<=q;++i){
		if(I[Q[i-1].a]!=I[Q[i].a]){
			tot=1;
			if(tp>=n)
				init();
			else
				while(tp)OUT();
			dn=LM[I[Q[i].a]];
		}
		while(tot<=m&&te[tot].b<=Q[i].b){
			if(te[tot].a<dn)
				IN(e[te[tot].a]);
			++tot;
		}
		int cp=tp;
		for(int j=dn;j<=Q[i].a;++j)
			if(e[j].b<=Q[i].b)
				IN(e[j]);
		int u=Ac(Q[i].u),v=Ac(Q[i].v);
		Ans[Q[i].id]=((u==v)&&(mx2[u]==e[Q[i].a].a)&&(mx3[u]==Q[i].b));
		while(tp>cp)
			OUT();
	}
	for(int i=1;i<=q;++i)
		puts(Ans[i]?"Yes":"No");
	return 0;
}

[HNOI2016]树：

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define ch() getchar()
#define pc(x) putchar(x)
using namespace std;
template<typename T>void read(T&x){
	static char c;static int f;
	for(c=ch(),f=1;c<'0'||c>'9';c=ch())if(c=='-')f=-f;
	for(x=0;c>='0'&&c<='9';c=ch())x=x*10+(c&15);x*=f;
}
template<typename T>void write(T x){
	static char q[65];int cnt=0;
	if(x<0)pc('-'),x=-x;
	q[++cnt]=x%10,x/=10;
	while(x)
		q[++cnt]=x%10,x/=10;
	while(cnt)pc(q[cnt--]+'0');
}
const int maxn=100005,maxm=100005,maxq=100005;
struct Edge{
	int v,nt;
	Edge(int v=0,int nt=0):
		v(v),nt(nt){}
}e[maxn*2+maxm];
int hd[maxn],num;
void qwq(int u,int v){
	e[++num]=Edge(v,hd[u]),hd[u]=num;
}
struct Node{
	int l,r,sz;
	Node(int l=0,int r=0,int sz=0):
		l(l),r(r),sz(sz){}
}P[maxn*50];
int tot;
int Merge(int x,int y){
	if(!x||!y)return x+y;int re=++tot;
	P[re]=Node(Merge(P[x].l,P[y].l),
			   Merge(P[x].r,P[y].r),
			   P[x].sz+P[y].sz);
	return re;
}
int build(int l,int r,int pos){
	int re=++tot;P[re]=Node(0,0,1);
	if(l==r)return re;int mid=(l+r)>>1;
	if(pos<=mid)P[re].l=build(l,mid,pos);
	else P[re].r=build(mid+1,r,pos);
	return re;
}
int query(int x,int l,int r,int k){
	if(l==r)return l;int mid=(l+r)>>1;
	if(k>P[P[x].l].sz)
		return query(P[x].r,mid+1,r,k-P[P[x].l].sz);
	return query(P[x].l,l,mid,k);
}
int rt[maxn],n,dis[maxn];
int pa[maxn][20],sz[maxn];
void dfs(int u,int fa){
	pa[u][0]=fa;
	for(int i=1;(1<<i)<=dis[u];++i)
		pa[u][i]=pa[pa[u][i-1]][i-1];
	rt[u]=build(1,n,u);sz[u]=1;
	for(int i=hd[u];i;i=e[i].nt){
		int v=e[i].v;if(v==fa)continue;
		dis[v]=dis[u]+1;dfs(v,u);
		rt[u]=Merge(rt[u],rt[v]);
		sz[u]+=sz[v];
	}
}
long long tim[maxm];int node[maxm];
void where(int l,int r,long long t,int&id0,int&id1){
	while(l<r){
		int mid=(l+r)>>1;
		if(tim[mid]>=t)r=mid;
		else l=mid+1;
	}
	id0=l=r;id1=query(rt[node[id0]],1,n,t-tim[id0-1]);
}
long long Dis[maxm];
long long DIS(int id0,int id1){
	return Dis[id0]+(dis[id1]-dis[node[id0]]);
}
int Dp[maxn],Pa[maxn][20],Ra[maxn][20];
int hds[maxn];
void qwqs(int u,int v){
	e[++num]=Edge(v,hds[u]);hds[u]=num;
	Dp[v]=Dp[u]+1;
}
void Dfs(int u,int fa){
	Pa[u][0]=fa;
	for(int i=1;(1<<i)<=Dp[u];++i)
		Pa[u][i]=Pa[Pa[u][i-1]][i-1],
		Ra[u][i]=Ra[Pa[u][i-1]][i-1];
	for(int i=hds[u];i;i=e[i].nt)
		Dfs(e[i].v,u);
}
void lca(int xid0,int xid1,int yid0,int yid1,int&zid0,int&zid1){
	if(Dp[xid0]<Dp[yid0])xid0^=yid0^=xid0^=yid0,xid1^=yid1^=xid1^=yid1;
	for(int t=Dp[xid0]-Dp[yid0],cn=0;t;t>>=1,++cn)
		if(t&1)xid1=Ra[xid0][cn],xid0=Pa[xid0][cn];
	if(xid0!=yid0){
		for(int t=18;t>=0;--t)
			if(Pa[xid0][t]!=Pa[yid0][t])
				xid1=Ra[xid0][t],yid1=Ra[yid0][t],
				xid0=Pa[xid0][t],yid0=Pa[yid0][t];
		xid1=Ra[xid0][0],yid1=Ra[yid0][0],
		xid0=Pa[xid0][0],yid0=Pa[yid0][0];
	}
	zid0=xid0=yid0;
	if(dis[xid1]<dis[yid1])xid1^=yid1^=xid1^=yid1;
	for(int t=dis[xid1]-dis[yid1],cn=0;t;t>>=1,++cn)
		if(t&1)xid1=pa[xid1][cn];
	if(xid1!=yid1){
		for(int t=18;t>=0;--t)
			if(pa[xid1][t]!=pa[yid1][t])
				xid1=pa[xid1][t],yid1=pa[yid1][t];
		xid1=pa[xid1][0],yid1=pa[yid1][0];
	}
	zid1=xid1=yid1;
}
int main(){
	int m,q;
	read(n),read(m),read(q);
	for(int i=1;i<n;++i){
		int u,v;
		read(u),read(v);
		qwq(u,v);qwq(v,u);
	}
	dfs(1,0);++m;
	tim[node[1]=1]=n;
	Dis[1]=0;Dp[1]=0;
	for(int i=2;i<=m;++i){
		int x;long long t;
		read(x),read(t);
		tim[i]=tim[i-1]+sz[x];
		int id0=0,id1=0;
		where(1,i-1,t,id0,id1);
		Dis[i]=DIS(id0,id1)+1;node[i]=x;
		qwqs(id0,i);Ra[i][0]=id1;
	}
	Dfs(1,0);
	while(q--){
		long long x,y;read(x),read(y);
		int xid0,xid1,yid0,yid1,zid0,zid1;
		where(1,m,x,xid0,xid1);
		where(1,m,y,yid0,yid1);
		lca(xid0,xid1,yid0,yid1,zid0,zid1);
		write(DIS(xid0,xid1)+DIS(yid0,yid1)-2*DIS(zid0,zid1));pc('\n');
	}
	return 0;
}

[HNOI2016]矿区：

#include<map>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define ch() getchar()
#define pc(x) putchar(x)
using namespace std;
template<typename T>void read(T&x){
	static char c;static int f;
	for(c=ch(),f=1;c<'0'||c>'9';c=ch())if(c=='-')f=-f;
	for(x=0;c>='0'&&c<='9';c=ch())x=x*10+(c&15);x*=f;
}
template<typename T>void write(T x){
	static char q[65];int cnt=0;
	if(x<0)pc('-'),x=-x;
	q[++cnt]=x%10,x/=10;
	while(x)
		q[++cnt]=x%10,x/=10;
	while(cnt)pc(q[cnt--]+'0');
}
const int maxn=600005,maxm=1200005,maxw=maxm;
struct Edge{
	int v,nt;
	Edge(int v=0,int nt=0):
		v(v),nt(nt){}
}e[maxm*2+maxm*2];
int hd[maxn],num=1;
map<pair<int,int>,int>TAT;
void qwq(int u,int v){
	e[++num]=Edge(v,hd[u]),TAT[pair<int,int>(u,v)]=hd[u]=num;
}
int hw[maxw];
void qaq(int u,int v){
	e[++num]=Edge(v,hw[u]),hw[u]=num;
}
struct Point{
	int x,y;
	Point(int x=0,int y=0):
		x(x),y(y){}
	int quadrant(void)const{
		return x<0?y<=0:y<0;
	}
}P[maxn];
typedef Point Vector;
Vector operator + (const Vector A,const Vector B){return Vector(A.x+B.x,A.y+B.y);}
Vector operator - (const Vector A,const Vector B){return Vector(A.x-B.x,A.y-B.y);}
long long Cro(const Vector A,const Vector B){return 1ll*A.x*B.y-1ll*A.y*B.x;}
bool cmp(const Vector A,const Vector B){
	return A.quadrant()^B.quadrant()?A.quadrant()<B.quadrant():Cro(A,B)>0;
}
struct TMP{
	Vector v;int id;
	TMP(Vector v=Vector(),int id=0):
		v(v),id(id){}
	bool operator < (const TMP o)const{
		return cmp(v,o.v);
	}
}Q[maxn];
int nt[maxm*2],vis[maxm*2];
long long s[maxw],s2[maxw];
int pa[maxw],dfn[maxw];
void addson(int u,int v){
	pa[v]=u;
}
long long sz[maxw],sz2[maxw];
void dfs(int u){
	dfn[u]=true;sz[u]=s[u];sz2[u]=s2[u];
	for(int i=hw[u];i;i=e[i].nt){
		int v=e[i].v;
		if(dfn[v])continue;
		addson(u,v);dfs(v);
		sz[u]+=sz[v];sz2[u]+=sz2[v];
	}
}
int z[maxm];
long long gcd(long long a,long long b){
	while(b){long long t=a%b;a=b;b=t;}return a;
}
int lock[maxw];
int main(){
	int n,m,k;
	read(n),read(m),read(k);
	for(int i=1;i<=n;++i)
		read(P[i].x),read(P[i].y);
	for(int i=1;i<=m;++i){
		int u,v;
		read(u),read(v);
		qwq(u,v),qwq(v,u);
	}
	for(int u=1;u<=n;++u){
		int tot=0;
		for(int i=hd[u];i;i=e[i].nt){
			int v=e[i].v;Q[++tot]=TMP(P[v]-P[u],i);
		}
		sort(Q+1,Q+tot+1);
		for(int i=1;i<tot;++i)
			nt[Q[i].id]=Q[i+1].id;
		nt[Q[tot].id]=Q[1].id;
	}
	for(int i=2;i<=num;i+=2)
		nt[i]^=nt[i^1]^=nt[i]^=nt[i^1];
	int cnt=0,root=0;
	for(int i=2;i<=num;++i){
		if(vis[i])continue;
		++cnt;int tmp=0;
		while(!vis[i]){
			s[cnt]+=Cro(P[e[i].v],P[e[i^1].v]);
			vis[i]=cnt;i=nt[i];
		}
		if(s[cnt]<=0)root=cnt,s[cnt]=0;
		s2[cnt]=s[cnt];s2[cnt]*=2;s[cnt]*=s[cnt];
	}
	int cp=num;
	for(int i=2;i<=cp;++i)
		qaq(vis[i],vis[i^1]);
	dfs(root);long long pre=0;
	while(k--){
		int c;read(c);
		int d=(c+pre)%n+1;
		for(int i=1;i<=d;++i)
			read(z[i]),z[i]=(z[i]+pre)%n+1;
		z[d+1]=z[1];
		long long up=0,dn=0;
		for(int i=1;i<=d;++i){
			int out=TAT[pair<int,int>(z[i],z[i+1])],in=out^1;z[i]=out;
			out=vis[out],in=vis[in];
			if((!lock[in]&&pa[in]==out)||(!lock[out]&&pa[out]==in)){
				if(!lock[out]&&pa[out]==in)up-=sz[out],dn-=sz2[out],lock[out]=true;
				else up+=sz[in],dn+=sz2[in],lock[in]=true;
			}
		}
		for(int i=1;i<=d;++i){
			int out=z[i],in=out^1;out=vis[out],in=vis[in];lock[out]=lock[in]=false;
		}
		long long tmp=gcd(up,dn);up/=tmp,dn/=tmp;
		write(pre=up),pc(' '),write(dn),pc('\n');pre%=n;
	}
	return 0;
}

[HNOI2016]网络：

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define ch() getchar()
#define pc(x) putchar(x)
using namespace std;
template<typename T>void read(T&x){
	static char c;static int f;
	for(c=ch(),f=1;c<'0'||c>'9';c=ch())if(c=='-')f=-f;
	for(x=0;c>='0'&&c<='9';c=ch())x=x*10+(c&15);x*=f;
}
template<typename T>void write(T x){
	static char q[65];int cnt=0;
	if(x<0)pc('-'),x=-x;
	q[++cnt]=x%10,x/=10;
	while(x)
		q[++cnt]=x%10,x/=10;
	while(cnt)pc(q[cnt--]+'0');
}
const int maxn=100005,maxm=200005;
struct Edge{
	int v,nt;
	Edge(int v=0,int nt=0):
		v(v),nt(nt){}
}e[maxn*2];
int hd[maxn],num;
void qwq(int u,int v){
	e[++num]=Edge(v,hd[u]),hd[u]=num;
}
int st[maxn*2][20],tp,pos[maxn];
int dfn[maxn],sz[maxn],dp[maxn],cnt;
void dfs(int u,int fa){
	dfn[u]=++cnt;sz[u]=1;
	st[pos[u]=++tp][0]=u;
	for(int i=hd[u];i;i=e[i].nt){
		int v=e[i].v;
		if(v==fa)continue;
		dp[v]=dp[u]+1;dfs(v,u);
		sz[u]+=sz[v];st[++tp][0]=u;
	}
}
int cmp(int x,int y){
	return dfn[x]<dfn[y]?x:y;
}
int lg2[maxn*2];
int lca(int x,int y){
	x=pos[x],y=pos[y];if(x>y)x^=y^=x^=y;int len=lg2[y-x+1];
	return cmp(st[x][len],st[y-(1<<len)+1][len]);
}
struct Line{
	int u,v;
	Line(int u=0,int v=0):
		u(u),v(v){}
	int nexist(void){
		return u==0&&v==0;
	}
	int all(void){
		return u==-1&&v==-1;
	}
	int in(int p){
		int w;return all()||(!nexist()&&(w=lca(u,v),dfn[w]<=dfn[p]&&dfn[p]<dfn[w]+sz[w]&&((dfn[p]<=dfn[u]&&dfn[u]<dfn[p]+sz[p])||(dfn[p]<=dfn[v]&&dfn[v]<dfn[p]+sz[p]))));
	}
};
int dpcmp(int x,int y){
	return dp[x]>dp[y];
}
int p[4];
Line cross(Line A,Line B){
	if(A.all())return B;if(B.all())return A;
	if(A.nexist()||B.nexist())return Line();
	p[0]=lca(A.u,B.u),p[1]=lca(A.u,B.v),
	p[2]=lca(A.v,B.u),p[3]=lca(A.v,B.v);
	sort(p,p+4,dpcmp);
	if(A.in(p[0])&&A.in(p[1])&&B.in(p[0])&&B.in(p[1]))
		return Line(p[0],p[1]);
	else
		return Line();
}
Line qaq[maxm*4];
void pushup(int x){
	qaq[x]=cross(qaq[x<<1],qaq[x<<1|1]);
}
void build(int x,int l,int r){
	qaq[x]=Line(-1,-1);if(l==r)return;int mid=(l+r)>>1;
	build(x<<1,l,mid);build(x<<1|1,mid+1,r);
}
void change(int x,int l,int r,int p,Line v){
	if(l==r)return qaq[x]=v,void();
	int mid=(l+r)>>1;
	if(p<=mid)change(x<<1,l,mid,p,v);
	else change(x<<1|1,mid+1,r,p,v);
	return pushup(x);
}
int query(int x,int l,int r,int p){
	if(l==r)return l;int mid=(l+r)>>1;
	if(qaq[x<<1|1].in(p))
		return query(x<<1,l,mid,p);
	return query(x<<1|1,mid+1,r,p);
}
struct temp{
	int id,val;
	temp(int id=0,int val=0):
		id(id),val(val){}
	bool operator < (const temp o)const{
		return val^o.val?val<o.val:id<o.id;
	}
}W[maxm];
int A[maxm],B[maxm],V[maxm],op[maxm];
int main(){
	int n,m;read(n),read(m);
	int mx=n*2;lg2[0]=-1;
	for(int i=1;i<=mx;++i)
		lg2[i]=lg2[i-1]+((i&(i-1))==0);
	for(int i=1;i<n;++i){
		int u,v;
		read(u),read(v);
		qwq(u,v),qwq(v,u);
	}
	dfs(1,0);
	for(int i=1;i<=lg2[tp];++i)
		for(int j=1;j+(1<<i)-1<=tp;++j)
			st[j][i]=cmp(st[j][i-1],st[j+(1<<(i-1))][i-1]);
	int cw=0;
	for(int i=1;i<=m;++i){
		read(op[i]);read(A[i]);if(op[i]==0)
		read(B[i]),read(V[i]),W[++cw]=temp(i,V[i]);
	}
	sort(W+1,W+cw+1);
	for(int i=1;i<=cw;++i)
		V[W[i].id]=i;
	build(1,1,cw);
	for(int i=1;i<=m;++i){
		if(op[i]==0)
			change(1,1,cw,V[i],Line(A[i],B[i]));
		else if(op[i]==1)
			change(1,1,cw,V[A[i]],Line(-1,-1));
		else{
			if(qaq[1].in(A[i]))puts("-1");
			else write(W[query(1,1,cw,A[i])].val),pc('\n');
		}
	}
	return 0;
}

[AHOI2017/HNOI2017]单旋：

#include<set>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define ch() getchar()
#define pc(x) putchar(x)
using namespace std;
template<typename T>void read(T&x){
	static char c;static int f;
	for(c=ch(),f=1;c<'0'||c>'9';c=ch())if(c=='-')f=-f;
	for(x=0;c>='0'&&c<='9';c=ch())x=x*10+(c&15);x*=f;
}
template<typename T>void write(T x){
	static char q[65];int cnt=0;
	if(x<0)pc('-'),x=-x;
	q[++cnt]=x%10,x/=10;
	while(x)
		q[++cnt]=x%10,x/=10;
	while(cnt)pc(q[cnt--]+'0');
}
const int maxn=100005;
struct Node{
	int s[2],p,sz;
	Node(int l=0,int r=0,int p=0,int sz=0){
		this->s[0]=l,this->s[1]=r;
		this->p=p,this->sz=sz;
	}
}P[maxn];
void pushup(int x){
	P[x].sz=P[P[x].s[0]].sz+P[P[x].s[1]].sz+1;
}
int isnroot(int x){
	return P[P[x].p].s[0]==x||P[P[x].p].s[1]==x;
}
int identify(int x){
	return P[P[x].p].s[1]==x;
}
void connect(int x,int f,int t){
	if(x)P[x].p=f;if(f)P[f].s[t]=x;
}
void rotate(int x){
	int p=P[x].p,t=identify(x);
	connect(P[x].s[!t],p,t);
	if(isnroot(p))connect(x,P[p].p,identify(p));
	else P[x].p=P[p].p;
	connect(p,x,!t);
	pushup(p);pushup(x);
}
void splay(int x){
	if(!x)return;
	while(isnroot(x)){
		int p=P[x].p;
		if(isnroot(p)){
			if(identify(p)==identify(x))
				rotate(p);
			else
				rotate(x);
		}
		rotate(x);
	}
}
void access(int x){
	for(int y=0;x;y=x,x=P[x].p){
		splay(x);P[x].s[1]=y;pushup(x);
	}
}
int tot;
struct VAL{
	int val,id;
	VAL(int val=0,int id=0):
		val(val),id(id){}
	bool operator < (const VAL o)const{
		return val^o.val?val<o.val:id<o.id;
	}
};
int son[maxn][2],fa[maxn],RT;
void link(int x,int f,int t){
	if(f)son[f][t]=x;if(x)fa[x]=f,P[x].p=f;
}
set<VAL>s;set<VAL>::iterator it;
int main(){
	int n;read(n);
	while(n--){
		int op;read(op);
		if(op==1){
			int key;read(key);++tot;P[tot].sz=1;
			it=s.insert(VAL(key,tot)).first;
			if(s.size()>1){
				if(it!=s.begin()){
					--it;
					if(!son[(*it).id][1]){
						link(tot,(*it).id,1);
					}
					++it;
				}
				++it;
				if(it!=s.end()){
					if(!son[(*it).id][0]){
						link(tot,(*it).id,0);
					}
				}
				--it;
			}
			else
				RT=tot;
			access(tot);splay(tot);
			write(P[tot].sz),pc('\n');
		}
		else if(op==2||op==4){
			it=s.begin();int now=(*it).id;
			access(now);splay(now);
			write(P[now].sz),pc('\n');
			splay(son[now][1]);
			link(son[now][1],fa[now],0);
			P[now].s[0]=P[P[now].s[0]].p=0;
			if(RT==now)RT=son[now][1];
			if(op==2){
				splay(RT);link(RT,now,1);
				fa[now]=0;RT=now;
			}
			else{
				s.erase(it);
			}
		}
		else{
			it=s.end();--it;int now=(*it).id;
			access(now);splay(now);
			write(P[now].sz),pc('\n');
			splay(son[now][0]);
			link(son[now][0],fa[now],1);
			P[now].s[0]=P[P[now].s[0]].p=0;
			if(RT==now)RT=son[now][0];
			if(op==3){
				splay(RT);link(RT,now,0);
				fa[now]=0;RT=now;
			}
			else{
				s.erase(it);
			}
		}
	}
	return 0;
}

[AHOI2017/HNOI2017]影魔：

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define ch() getchar()
#define pc(x) putchar(x)
using namespace std;
template<typename T>void read(T&x){
	static char c;static int f;
	for(c=ch(),f=1;c<'0'||c>'9';c=ch())if(c=='-')f=-f;
	for(x=0;c>='0'&&c<='9';c=ch())x=x*10+(c&15);x*=f;
}
template<typename T>void write(T x){
	static char q[65];int cnt=0;
	if(x<0)pc('-'),x=-x;
	q[++cnt]=x%10,x/=10;
	while(x)
		q[++cnt]=x%10,x/=10;
	while(cnt)pc(q[cnt--]+'0');
}
const int maxn=200005,maxm=200005;
int n;
struct TREE{
	long long tr[maxn];
	void change(int pos,long long val){
		while(pos){
			tr[pos]+=val;
			pos^=pos&(-pos);
		}
	}
	long long query(int pos){
		long long re=0;
		while(pos<=n){
			re+=tr[pos];
			pos+=pos&(-pos);
		}
		return re;
	}
}T0,T1;
struct SegmentTree{
	long long val[maxn<<2],tag[maxn<<2],len[maxn<<2];
	void build(int x,int l,int r){
		len[x]=r-l+1;val[x]=tag[x]=0;if(l==r)return;
		int mid=(l+r)>>1;build(x<<1,l,mid);build(x<<1|1,mid+1,r);
	}
	void push(int x,long long v){
		val[x]+=v*len[x],tag[x]+=v;
	}
	void pushup(int x){
		val[x]=val[x<<1]+val[x<<1|1];
	}
	void pushdown(int x){
		push(x<<1,tag[x]);
		push(x<<1|1,tag[x]);
		tag[x]=0;
	}
	void change(int x,int l,int r,int L,int R,long long v){
		if(L>R)return;
		if(L<=l&&r<=R)return push(x,v);
		pushdown(x);int mid=(l+r)>>1;
		if(L<=mid)change(x<<1,l,mid,L,R,v);
		if(R>mid)change(x<<1|1,mid+1,r,L,R,v);
		return pushup(x);
	}
	long long query(int x,int l,int r,int L,int R){
		if(L>R)return 0;
		if(L<=l&&r<=R)return val[x];
		pushdown(x);int mid=(l+r)>>1;long long re=0;
		if(L<=mid)re+=query(x<<1,l,mid,L,R);
		if(R>mid)re+=query(x<<1|1,mid+1,r,L,R);
		return re;
	}
}T2;
struct Edge{
	int v,w,nt;
	Edge(int v=0,int w=0,int nt=0):
		v(v),w(w),nt(nt){}
}e[maxm];
int hd[maxn],num;
void qwq(int u,int v,int w){
	e[++num]=Edge(v,w,hd[u]),hd[u]=num;
}
int k[maxn];
long long Ans[maxm];
int st[maxn];
int main(){
	int m;long long p1,p2;
	read(n),read(m),read(p1),read(p2);
	for(int i=1;i<=n;++i)read(k[i]);
	for(int i=1;i<=m;++i){
		int l,r;
		read(l),read(r);
		qwq(r,l,i);
	}
	int tp=0;T2.build(1,0,n);
	for(int i=1;i<=n;++i){
		while(tp&&k[st[tp]]<k[i]){
			T2.change(1,0,n,st[tp],st[tp],p1-p2);
			--tp;if(tp>0){
				T0.change(st[tp],-p2);
				T1.change(st[tp],-p2*i);
			}
		}
		T2.change(1,0,n,st[tp],st[tp],p1-p2);
		T2.change(1,0,n,st[tp],i-1,p2);
		for(int j=hd[i];j;j=e[j].nt){
			int v=e[j].v,w=e[j].w;
			Ans[w]=T0.query(v)*(i+1)-T1.query(v)+T2.query(1,0,n,v,i);
		}
		T0.change(st[tp],p2);
		T1.change(st[tp],p2*(i+1));
		st[++tp]=i;
	}
	for(int i=1;i<=m;++i)
		write(Ans[i]),pc('\n');
	return 0;
}

[AHOI2017/HNOI2017]礼物：

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define ch() getchar()
#define pc(x) putchar(x)
using namespace std;
template<typename T>void read(T&x){
	static char c;static int f;
	for(c=ch(),f=1;c<'0'||c>'9';c=ch())if(c=='-')f=-f;
	for(x=0;c>='0'&&c<='9';c=ch())x=x*10+(c&15);x*=f;
}
template<typename T>void write(T x){
	static char q[65];int cnt=0;
	if(x<0)pc('-'),x=-x;
	q[++cnt]=x%10,x/=10;
	while(x)
		q[++cnt]=x%10,x/=10;
	while(cnt)pc(q[cnt--]+'0');
}
const int mod=998244353,maxn=50005,saxn=400005,g_=3;
int mo(const int x){
	return x>=mod?x-mod:x;
}
int power(int a,int x){
	int re=1;
	while(x){
		if(x&1)re=1ll*re*a%mod;
		a=1ll*a*a%mod,x>>=1;
	}
	return re;
}
int rev[saxn];
void NTT(int*F,int n,int rv){
	for(int i=0;i<n;++i)if(rev[i]<i)
		F[rev[i]]^=F[i]^=F[rev[i]]^=F[i];
	for(int mid=1;mid<n;mid<<=1){
		int len=mid<<1,gn=power(g_,(mod-1)/len);
		for(int i=0;i<n;i+=len){
			for(int j=0,g=1;j<mid;++j,g=1ll*g*gn%mod){
				int l=i+j,r=l+mid;
				int L=F[l],R=1ll*F[r]*g%mod;
				F[l]=mo(L+R),F[r]=mo(mod-R+L);
			}
		}
	}
	if(!rv)return;reverse(F+1,F+n);int I=power(n,mod-2);
	for(int i=0;i<n;++i)F[i]=1ll*F[i]*I%mod;
}
int x[saxn],y[saxn];
int main(){
	int n,m;read(n),read(m);
	for(int i=0;i<n;++i)read(x[i]);
	for(int i=0;i<n;++i)read(y[i]);
	reverse(y,y+n);
	int sx=0,sy=0,s2x=0,s2y=0;
	for(int i=0;i<n;++i)
		sx+=x[i],s2x+=x[i]*x[i];
	for(int i=0;i<n;++i)
		sy+=y[i],s2y+=y[i]*y[i];
	int delta=sy-sx,cut=delta%n;
	if(cut<0)cut+=n;
	if(cut<=n-cut)delta-=cut;
	else delta+=n-cut;
	delta/=n;
	long long ans=s2x+s2y+1ll*delta*delta*n+2ll*delta*(sx-sy);
	int cn=-1,N=1;while(N<(n*2))N<<=1,++cn;
	for(int i=1;i<N;++i)rev[i]=(rev[i>>1]>>1)|((i&1)<<cn);
	NTT(x,N,0);NTT(y,N,0);for(int i=0;i<N;++i)x[i]=1ll*x[i]*y[i]%mod;NTT(x,N,1);
	long long sum=-0x3f3f3f3f3f3f3f3fll;for(int i=0;i<n;++i)sum=max(sum,1ll*(x[n-1-i]+x[n*2-1-i]));
	write(ans-sum*2);pc('\n');
	return 0;
}

[AHOI2017/HNOI2017]大佬：

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define ch() getchar()
#define pc(x) putchar(x)
#define inf 0x3f3f3f3f
using namespace std;
template<typename T>void read(T&x){
	static char c;static int f;
	for(c=ch(),f=1;c<'0'||c>'9';c=ch())if(c=='-')f=-f;
	for(x=0;c>='0'&&c<='9';c=ch())x=x*10+(c&15);x*=f;
}
template<typename T>void write(T x){
	static char q[65];int cnt=0;
	if(x<0)pc('-'),x=-x;
	q[++cnt]=x%10,x/=10;
	while(x)
		q[++cnt]=x%10,x/=10;
	while(cnt)pc(q[cnt--]+'0');
}
const int maxs=8000005,mod=9982443,maxn=105;
struct TEMP{
	int D,F,L;
	TEMP(int D=0,int F=0,int L=0):
		D(D),F(F),L(L){}
	bool operator < (const TEMP o)const{
		return F^o.F?F<o.F:D^o.D?D<o.D:L<o.L;
	}
}Q[maxs];
struct Edge{
	int F,L,nt;
	Edge(int F=0,int L=0,int nt=0):
		F(F),L(L),nt(nt){}
}e[maxs];
int hd[mod],num;
void qwq(int u,int F,int L){
	e[++num]=Edge(F,L,hd[u]),hd[u]=num;
}
int vised(int F,int L){
	int tmp=F%mod;
	for(int i=hd[tmp];i;i=e[i].nt){
		if(e[i].F==F&&e[i].L==L)return true;
	}
	qwq(tmp,F,L);return false;
}
int a[maxn],w[maxn];
int dp[maxn][maxn];
int main(){
	int n,m,mc;
	read(n),read(m),read(mc);
	for(int i=1;i<=n;++i)read(a[i]);
	for(int i=1;i<=n;++i)read(w[i]);
	memset(dp,-1,sizeof dp);dp[0][0]=mc;
	for(int i=1;i<=n;++i){
		for(int j=0;j<=i;++j){
			if(dp[i-1][j]>=a[i])dp[i][j]=max(dp[i][j],dp[i-1][j]-a[i]);
			if(j>0&&dp[i-1][j-1]>=a[i])dp[i][j]=max(dp[i][j],min(mc,dp[i-1][j-1]-a[i]+w[i]));
		}
	}
	int days=-1;
	for(int i=1;i<=n;++i){
		int no=0;
		while(no<=i&&dp[i][no]==-1)++no;
		if(no<=i)days=max(days,i-no);
	}
	int fro=0,bac=0;
	Q[bac++]=TEMP(0,1,0);vised(1,0);
	while(fro!=bac){
		TEMP tmp=Q[fro++];
		if(tmp.D>=days-1)continue;
		if(1ll*tmp.F*tmp.L<=100000000&&tmp.L>0&&!vised(tmp.F*tmp.L,tmp.L))
			Q[bac++]=TEMP(tmp.D+1,tmp.F*tmp.L,tmp.L);
		if(1ll*tmp.F*(tmp.L+1)<=100000000&&!vised(tmp.F,tmp.L+1))
			Q[bac++]=TEMP(tmp.D+1,tmp.F,tmp.L+1);
	}
	sort(Q,Q+fro);int tot=0;
	for(int i=0;i<fro;++i)
		if(i==0||Q[i].F!=Q[i-1].F)
			Q[tot++]=Q[i];
	while(m--){
		int C;read(C);int ok=false;
		for(int i=0;i<tot&&!ok;++i)
			if(Q[i].F<=C&&Q[i].F+days-1-Q[i].D>=C)ok=true;
		int no=0,mx=-inf;
		for(int i=tot-1;i>=0&&!ok;--i){
			while(no<tot&&Q[no].F+Q[i].F<=C)
				mx=max(mx,Q[no].F-Q[no].D),++no;
			if(Q[i].F-Q[i].D+days-2+mx>=C)
				ok=true;
		}
		puts(ok?"1":"0");
	}
	return 0;
}

[AHOI2017/HNOI2017]队长快跑：

#include<cmath>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define ch() getchar()
#define pc(x) putchar(x)
using namespace std;
template<typename T>void read(T&x){
	static char c;static int f;
	for(c=ch(),f=1;c<'0'||c>'9';c=ch())if(c=='-')f=-f;
	for(x=0;c>='0'&&c<='9';c=ch())x=x*10+(c&15);x*=f;
}
template<typename T>void write(T x){
	static char q[65];int cnt=0;
	if(x<0)pc('-'),x=-x;
	q[++cnt]=x%10,x/=10;
	while(x)
		q[++cnt]=x%10,x/=10;
	while(cnt)pc(q[cnt--]+'0');
}
const int maxn=1000005;
const double eps=1e-15;
int dcmp(const double A,const double B){
	return fabs(A-B)<=eps?0:A>B?1:-1;
}
struct Point{
	double x,y;
	Point(double x=0.0,double y=0.0):
		x(x),y(y){}
	bool operator < (const Point o)const{
		return dcmp(x,o.x)?dcmp(x,o.x)<0:dcmp(y,o.y)<0;
	}
	bool operator == (const Point o)const{
		return dcmp(x,o.x)==0&&dcmp(y,o.y)==0;
	}
	double dis(void){
		return sqrt(x*x+y*y);
	}
};
typedef Point Vector;
Vector operator + (const Vector A,const Vector B){return Vector(A.x+B.x,A.y+B.y);}
Vector operator - (const Vector A,const Vector B){return Vector(A.x-B.x,A.y-B.y);}
Vector operator * (const Vector A,const double B){return Vector(A.x*B  ,A.y*B  );}
Vector operator / (const Vector A,const double B){return Vector(A.x/B  ,A.y/B  );}
double Cro(const Vector A,const Vector B){return A.x*B.y-A.y*B.x;}
Vector Rotate(const Vector A,const double B){return Vector(A.x*cos(B)-A.y*sin(B),A.x*sin(B)+A.y*cos(B));}
double Dis(const Point A,const Point B){return (A-B).dis();}
const Vector BASE(1e3,0.0);
struct Line{
	Point p;Vector v;
	Line(Point p=Point(),Vector v=Vector()):
		p(p),v(v){}
	void move(void){
//		p=p+v*eps;
	}
	bool operator < (const Line o)const{
		return p==o.p?v<o.v:p<o.p;
	}
	bool operator == (const Line o)const{
		return p==o.p&&v==o.v;
	}
}L[maxn];
int Q[2][maxn],FRO[2],BAC[2];
int JUDGE(Point A,Point B,Point C,int o){
	return (dcmp(Cro(C-A,B-A),0.0)>=0)^o;
}
double VAL[2];
int main(){
	int n;Point QAQ(0.0,0.0),QWQ;
	read(n);scanf("%lf%lf",&QWQ.x,&QWQ.y);
	for(int i=1;i<=n;++i){
		double theta;
		scanf("%lf%lf%lf",&L[i].p.x,&L[i].p.y,&theta);
		L[i].v=Rotate(BASE,theta);L[i].move();
		if(L[i].p.x<=QAQ.x||L[i].p.x>=QWQ.x){--i,--n;}
	}
	sort(L+1,L+n+1);
	n=unique(L+1,L+n+1)-(L+1);
	double ans=0.0;
	for(int t=0;t<2;++t){
		FRO[t]=1,BAC[t]=0;
		Q[t][++BAC[t]]=0;
	}
	for(int i=1;i<=n;++i){
		int o=(dcmp(L[i].v.x,0.0)<0?dcmp(Cro(QAQ-L[i].p,L[i].v),0.0)>0:dcmp(Cro(L[i].v,QWQ-L[i].p),0.0)>0);
		while(BAC[o]-FRO[o]>=1&&JUDGE(L[Q[o][BAC[o]-1]].p,L[Q[o][BAC[o]]].p,L[i].p,o))--BAC[o];
		while(BAC[!o]-FRO[!o]>=1&&JUDGE(L[Q[!o][FRO[!o]]].p,L[Q[!o][FRO[!o]+1]].p,L[i].p,o))
			ans+=Dis(L[Q[!o][FRO[!o]]].p,L[Q[!o][FRO[!o]+1]].p),++FRO[!o];
		Q[o][FRO[o]]=Q[!o][FRO[!o]];Q[o][++BAC[o]]=i;
	}
	for(int o=0;o<2;++o){
		while(BAC[o]-FRO[o]>=1&&JUDGE(L[Q[o][BAC[o]-1]].p,L[Q[o][BAC[o]]].p,QWQ,o))--BAC[o];
		for(int i=FRO[o];i<BAC[o];++i)VAL[o]+=Dis(L[Q[o][i]].p,L[Q[o][i+1]].p);
		VAL[o]+=Dis(L[Q[o][BAC[o]]].p,QWQ);
	}
	ans+=max(VAL[0],VAL[1]);
	printf("%.100f\n",ans);
	return 0;
}

[AHOI2018/HNOI2017]抛硬币：

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define ch() getchar()
#define pc(x) putchar(x)
using namespace std;
template<typename T>void read(T&x){
	static char c;static int f;
	for(c=ch(),f=1;c<'0'||c>'9';c=ch())if(c=='-')f=-f;
	for(x=0;c>='0'&&c<='9';c=ch())x=x*10+(c&15);x*=f;
}
template<typename T>void write(T x){
	static char q[65];int cnt=0;
	if(x<0)pc('-'),x=-x;
	q[++cnt]=x%10,x/=10;
	while(x)
		q[++cnt]=x%10,x/=10;
	while(cnt)pc(q[cnt--]+'0');
}
void exgcd(int x,int y,long long&a,long long&b){
	if(y==0)return a=1,b=0,void();
	exgcd(y,x%y,b,a);b-=a*(x/y);
}
const int p0=2,p1=5;
int mod,mod0,mod1,inv0,inv1,f0[1500],f1[10000000];
const int MX0=1024,MX1=9765625;
inline int mo(const int x){return x>=mod?x-mod:x;}
inline int mo0(const int x){return x>=mod0?x-mod0:x;}
inline int mo1(const int x){return x>=mod1?x-mod1:x;}
void init(int k){
	mod0=1,mod1=1;
	for(int i=1;i<=k;++i)
		mod0*=p0,mod1*=p1;
	mod=mod0*mod1;
	long long a,b;
	exgcd(mod0,mod1,a,b);
	a-=a/mod1;a=mo1(a+mod1);a=mo1(a+mod1);
	b-=b/mod0;b=mo0(b+mod0);b=mo0(b+mod0);
	inv0=a,inv1=b;
}
int Inv0(int x){
	long long a,b;exgcd(x,mod0,a,b);
	a-=a/mod0;a=mo0(a+mod0);a=mo0(a+mod0);
	return a;
}
int Inv1(int x){
	long long a,b;exgcd(x,mod1,a,b);
	a-=a/mod1;a=mo1(a+mod1);a=mo1(a+mod1);
	return a;
}
inline int power0(int a,long long x){
	if(x<0)a=Inv0(a),x=-x;
	int re=1;
	while(x){
		if(x&1)re=1ll*re*a%mod0;
		a=1ll*a*a%mod0,x>>=1;
	}
	return re;
}
inline int power1(int a,long long x){
	if(x<0)a=Inv1(a),x=-x;
	int re=1;
	while(x){
		if(x&1)re=1ll*re*a%mod1;
		a=1ll*a*a%mod1,x>>=1;
	}
	return re;
}
inline int F0(long long n){
	int re=1;while(n)re=1ll*re*power0(f0[mod0-1]%mod0,n/mod0)*(f0[n%mod0]%mod0)%mod0,n/=p0;return re;
}
inline int F1(long long n){
	int re=1;while(n)re=1ll*re*power1(f1[mod1-1]%mod1,n/mod1)*(f1[n%mod1]%mod1)%mod1,n/=p1;return re;
}
struct Int{
	int v0,v1;Int(int v0=0,int v1=0):v0(v0),v1(v1){}
	Int operator + (const Int o)const{return Int(mo0(v0+o.v0),mo1(v1+o.v1));}
	Int operator - (const Int o)const{return Int(mo0(mod0-o.v0+v0),mo1(mod1-o.v1+v1));}
	Int operator * (const Int o)const{return Int(1ll*v0*o.v0%mod0,1ll*v1*o.v1%mod1);}
	int val(void){return mo(1ll*v0*mod1%mod*inv1%mod+1ll*v1*mod0%mod*inv0%mod);}
};
struct BINOM{
	int v0,v1;long long cnt0,cnt1;
	void init(long long n,long long m){
		long long cut=n-m;
		cnt0=0;for(long long tmp=p0;n/tmp;tmp*=p0)cnt0+=n/tmp-m/tmp-cut/tmp;
		v0=1ll*F0(n)*Inv0(F0(m))%mod0*Inv0(F0(n-m))%mod0;
		cnt1=0;for(long long tmp=p1;n/tmp;tmp*=p1)cnt1+=n/tmp-m/tmp-cut/tmp;
		v1=1ll*F1(n)*Inv1(F1(m))%mod1*Inv1(F1(n-m))%mod1;
	}
	void qaq(long long qwq,int o){
		long long cp=0;
		cp=qwq;while(cp%p0==0)cnt0+=o,cp/=p0;cp%=mod0;
		v0=1ll*v0*power0(cp,o)%mod0;
		cp=qwq;while(cp%p1==0)cnt1+=o,cp/=p1;cp%=mod1;
		v1=1ll*v1*power1(cp,o)%mod1;
	}
	Int val(void){return Int(1ll*v0*power0(p0,cnt0)%mod0,1ll*v1*power1(p1,cnt1)%mod1);}
}B0,B1;
inline Int power(Int a,long long x){
	Int re(1,1);
	while(x){
		if(x&1)re=re*a;
		a=a*a,x>>=1;
	}
	return re;
}
int main(){
	f0[0]=1;
	for(int i=1;i<MX0;++i)
		f0[i]=1ll*f0[i-1]*(i%p0==0?1:i)%MX0;
	f1[0]=1;
	for(int i=1;i<MX1;++i)
		f1[i]=1ll*f1[i-1]*(i%p1==0?1:i)%MX1;
	long long a,b;int k;
	while(~scanf("%lld%lld%d",&a,&b,&k)){
		init(k);Int ans(0,0);B0.init(2*b-1,b-1);
		Int sum=power(Int(2%mod0,2%mod1),2*b-1)-B0.val();
		for(int t=0;;){
			if(t==0)B0.init(a-b,0);
			else B0.qaq(a-b-t+1,1),B0.qaq(t,-1);
			ans=ans+B0.val()*sum;
			if(b+t==a)break;++t;
			if(b+t-1>2*b)continue;
			if(t==1)B1.init(2*b,b+t-1);
			else B1.qaq(b-t+2,1),B1.qaq(b+t-1,-1);
			sum=sum+B1.val();
		}
		printf("%0*d\n",k,ans.val());
	}
	return 0;
}

[AHOI2018/HNOI2018]寻宝游戏：

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define ch() getchar()
#define pc(x) putchar(x)
#define inf 0x3f3f3f3f
using namespace std;
template<typename T>void read(T&x){
	static char c;static int f;
	for(c=ch(),f=1;c<'0'||c>'9';c=ch())if(c=='-')f=-f;
	for(x=0;c>='0'&&c<='9';c=ch())x=x*10+(c&15);x*=f;
}
template<typename T>void write(T x){
	static char q[65];int cnt=0;
	if(x<0)pc('-'),x=-x;
	q[++cnt]=x%10,x/=10;
	while(x)
		q[++cnt]=x%10,x/=10;
	while(cnt)pc(q[cnt--]+'0');
}
const int maxm=5005,maxn=1005,maxq=1005,maxs=maxn*maxm,mod=1000000007;
inline int mo(const int x){return x>=mod?x-mod:x;}
inline void chkmin(int&x,int y){x=min(x,y);}
inline void chkmax(int&x,int y){x=max(x,y);}
int son[maxs][2],tot,dfn[maxs],cnt;
int L[maxs],R[maxs];
void dfs(int u){
	L[u]=inf,R[u]=-inf;if(!u)return;
	if(!son[u][0]&&!son[u][1]){
		dfn[u]=++cnt;return;
	}
	dfs(son[u][0]);
	dfs(son[u][1]);
}
void LAR(int u){
	if(son[u][0]){LAR(son[u][0]);chkmin(L[u],L[son[u][0]]),chkmax(R[u],R[son[u][0]]);}
	if(son[u][1]){LAR(son[u][1]);chkmin(L[u],L[son[u][1]]),chkmax(R[u],R[son[u][1]]);}
}
int _2[maxn];int ed[maxm];
bool cmp(int x,int y){return dfn[ed[x]]<dfn[ed[y]];}
int id[maxm];char A[maxn][maxm];char T[maxm];int sum[2][maxm];
int CNT(int x,int o){return x?(sum[o][R[x]]-sum[o][L[x]-1]):0;}
int solve(int l,int r,int dp){
	//l->0 r->1s
	//CNT(l,0) CNT(r,1)
	if(dp==0)return CNT(r,1)==0;
	if(CNT(l,0)==0&&CNT(r,1)==0)return _2[dp];int re=0;
	int cA=CNT(son[l][1],0),cO=CNT(son[r][0],1);
	if(!cO)re=mo(re+solve(son[l][1],son[r][1],dp-1));
	if(!cA)re=mo(re+solve(son[l][0],son[r][0],dp-1));
	return re;
}
int main(){
	int n,m,q;
	read(n),read(m),read(q);
	_2[0]=1;
	for(int i=1;i<=n;++i)
		scanf("%s",A[i]+1),_2[i]=mo(_2[i-1]<<1);
	tot=1;
	for(int i=1;i<=m;++i){
		int now=1;
		for(int j=n;j>=1;--j){
			int o=(A[j][i]&1);
			if(!son[now][o])son[now][o]=++tot;
			now=son[now][o];
		}
		ed[i]=now;
		id[i]=i;
	}
	dfs(1);
	sort(id+1,id+m+1,cmp);
	for(int i=1;i<=m;++i){
		int node=ed[id[i]];
		chkmin(L[node],i);
		chkmax(R[node],i);
	}
	LAR(1);
	for(int i=1;i<=q;++i){
		scanf("%s",T+1);
		for(int j=1;j<=m;++j){
			sum[0][j]=sum[1][j]=0;
			++sum[T[id[j]]&1][j];
			sum[0][j]+=sum[0][j-1];
			sum[1][j]+=sum[1][j-1];
		}
		write(solve(1,1,n)),pc('\n');
	}
	return 0;
}

[AHOI2018/HNOI2018]转盘：

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define ch() getchar()
#define pc(x) putchar(x)
using namespace std;
template<typename T>void read(T&x){
	static char c;static int f;
	for(c=ch(),f=1;c<'0'||c>'9';c=ch())if(c=='-')f=-f;
	for(x=0;c>='0'&&c<='9';c=ch())x=x*10+(c&15);x*=f;
}
template<typename T>void write(T x){
	static char q[65];int cnt=0;
	if(x<0)pc('-'),x=-x;
	q[++cnt]=x%10,x/=10;
	while(x)
		q[++cnt]=x%10,x/=10;
	while(cnt)pc(q[cnt--]+'0');
}
const int maxn=100005,maxm=100005;
struct value{
	int val,pos,mn;
	value(int val=0,int pos=0,int mn=0):
		val(val),pos(pos),mn(mn){}
	bool operator == (const value o)const{
		return val==o.val&&pos==o.pos&&mn==o.mn;
	}
};
const value EmptyValue(-1,-1,-1);
value operator + (const value L,const value R){
	return L==EmptyValue?R:R==EmptyValue?L:value(L.val,R.pos,min(min(L.mn,R.mn),L.pos+R.val));
}
int mx[maxn*4];
value vx[maxn*4];
value query(int x,int l,int r,int v){
	if(l==r)return mx[x]>=v?value(mx[x],l=r,0x3f3f3f3f):EmptyValue;
	int mid=(l+r)>>1;if(v<=mx[x<<1|1])
		return vx[x]+query(x<<1|1,mid+1,r,v);
	return query(x<<1,l,mid,v);
}
void pushup(int x,int l,int r){
	int mid=(l+r)>>1;
	vx[x]=query(x<<1,l,mid,mx[x<<1|1]);
	mx[x]=max(mx[x<<1],mx[x<<1|1]);
}
void build(int x,int l,int r){
	if(l==r)return read(mx[x]),mx[x]-=(l=r),void();
	int mid=(l+r)>>1;
	build(x<<1,l,mid);
	build(x<<1|1,mid+1,r);
	return pushup(x,l,r);
}
void change(int x,int l,int r,int p,int v){
	if(l==r)return mx[x]=v,void();int mid=(l+r)>>1;
	if(p<=mid)change(x<<1,l,mid,p,v);
	else change(x<<1|1,mid+1,r,p,v);
	pushup(x,l,r);
}
value query(int x,int l,int r,int L,int R,int v){
	if(L<=l&&r<=R)return query(x,l,r,v);int mid=(l+r)>>1;
	if(R>mid&&L<=mid)
		return query(x<<1,l,mid,L,R,max(v,mx[x<<1|1]))+query(x<<1|1,mid+1,r,L,R,v);
	if(L<=mid)return query(x<<1,l,mid,L,R,v);
	if(R>mid)return query(x<<1|1,mid+1,r,L,R,v);
	return value();
}
int whereL(int x,int l,int r,int v){
	if(l==r)return l;int mid=(l+r)>>1;
	if(mx[x<<1]>=v)
		return whereL(x<<1,l,mid,v);
	return whereL(x<<1|1,mid+1,r,v);
}
int whereR(int x,int l,int r,int v){
	if(l==r)return r;int mid=(l+r)>>1;
	if(mx[x<<1|1]>=v)
		return whereR(x<<1|1,mid+1,r,v);
	return whereR(x<<1,l,mid,v);
}
int T[maxn],n;
int solve(void){
	int S=mx[1];
	value tmp=query(1,1,n,whereL(1,1,n,S),whereR(1,1,n,S-n),-0x3f3f3f3f);
	return n+min(min(0,tmp.pos-n)+S,tmp==EmptyValue?0x3f3f3f3f:tmp.mn);
}
int main(){
	int m,p;
	read(n),read(m),read(p);
	build(1,1,n);int la=0;
	write(la=solve()),pc('\n');
	for(int i=1;i<=m;++i){
		int x,y;
		read(x),read(y);
		if(p)x^=la,y^=la;
		change(1,1,n,x,y-x);
		write(la=solve()),pc('\n');
	}
	return 0;
}

[AHOI2018/HNOI2018]毒瘤：

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define ch() getchar()
#define pc(x) putchar(x)
using namespace std;
template<typename T>void read(T&x){
	static char c;static int f;
	for(c=ch(),f=1;c<'0'||c>'9';c=ch())if(c=='-')f=-f;
	for(x=0;c>='0'&&c<='9';c=ch())x=x*10+(c&15);x*=f;
}
template<typename T>void write(T x){
	static char q[65];int cnt=0;
	if(x<0)pc('-'),x=-x;
	q[++cnt]=x%10,x/=10;
	while(x)
		q[++cnt]=x%10,x/=10;
	while(cnt)pc(q[cnt--]+'0');
}
const int maxn=100005,maxm=maxn+10,mod=998244353;
int mo(const int x){
	return x>=mod?x-mod:x;
}
int power(int a,int x){
	int re=1;
	while(x){
		if(x&1)re=1ll*re*a%mod;
		a=1ll*a*a%mod,x>>=1;
	}
	return re;
}
struct Edge{
	int v,nt;
	Edge(int v=0,int nt=0):
		v(v),nt(nt){}
}e[maxm*2];
int hd[maxn],num;
void qwq(int u,int v){
	e[++num]=Edge(v,hd[u]),hd[u]=num;
}
int son[maxn],bro[maxn],pa[maxn];
void addson(int u,int v){
	bro[v]=son[u],son[u]=v,pa[v]=u;
}
int vis[maxn],S[15],T[15],cnt;
void dfs(int u,int fa){
	vis[u]=1;
	for(int i=hd[u];i;i=e[i].nt){
		int v=e[i].v;
		if(v==fa)continue;
		if(vis[v]==1){
			++cnt;
			S[cnt]=u;
			T[cnt]=v;
		}
		if(vis[v])continue;
		addson(u,v);dfs(v,u);
	}
	vis[u]=2;
}
int test,f[maxn][2],zero[maxn][2];
int val(int u,int t){
	return zero[u][t]>0?0:f[u][t];
}
void INS(int u,int v){
	test=mo(val(v,0)+val(v,1));
	if(test)f[u][0]=1ll*f[u][0]*test%mod;
	else ++zero[u][0];
	test=val(v,0);
	if(test)f[u][1]=1ll*f[u][1]*test%mod;
	else ++zero[u][1];
}
void DEL(int u,int v){
	test=mo(val(v,0)+val(v,1));
	if(test)f[u][0]=1ll*f[u][0]*power(test,mod-2)%mod;
	else --zero[u][0];
	test=val(v,0);
	if(test)f[u][1]=1ll*f[u][1]*power(test,mod-2)%mod;
	else --zero[u][1];
}
int sz[maxn],hs[maxn];
void dfs0(int u){
	sz[u]=f[u][0]=f[u][1]=1;int mx=0;
	for(int v=son[u];v;v=bro[v]){
		dfs0(v);sz[u]+=sz[v];INS(u,v);
		if(sz[v]>mx)mx=sz[hs[u]=v];
	}
}
struct Matrix{
	int v[2][2];
	Matrix(int v00=0,int v01=0,int v10=0,int v11=0){
		this->v[0][0]=v00,this->v[0][1]=v01;
		this->v[1][0]=v10,this->v[1][1]=v11;
	}
	int*operator [] (const int o){
		return v[o];
	}
}M[1<<20];
int K,top[maxn],dfn[maxn],mx[maxn],owo;
void dfs1(int u){
	dfn[u]=++owo;
	mx[top[u]]=max(mx[top[u]],dfn[u]);
	if(hs[u]){
		top[hs[u]]=top[u];
		DEL(u,hs[u]);
		dfs1(hs[u]);
	}
	for(int v=son[u];v;v=bro[v]){
		if(v==hs[u])continue;dfs1(top[v]=v);
	}
	M[dfn[u]|(1<<K)]=Matrix(val(u,0),val(u,1),val(u,0),0);
}
Matrix operator * (Matrix A,Matrix B){
	Matrix re(0,0,0,0);
	for(int i=0;i<2;++i)for(int j=0;j<2;++j)for(int k=0;k<2;++k)
		re[i][j]=mo(re[i][j]+1ll*A[i][k]*B[k][j]%mod);
	return re;
}
Matrix query(int l,int r){
	--l,++r;l|=1<<K,r|=1<<K;
	Matrix L(1,0,0,1),R(1,0,0,1);
	while(l^r^1){
		if(!(l&1))L=M[l^1]*L;
		if( (r&1))R=R*M[r^1];
		l>>=1,r>>=1;
	}
	return R*L;
}
void pushup(int x){
	M[x]=M[x<<1|1]*M[x<<1];
}
int cov[maxn],n;
void change(int x){
	while(x){
		if(pa[top[x]]){
			Matrix tmp=query(dfn[top[x]],mx[top[x]]);
			f[n+1][0]=tmp[0][0],f[n+1][1]=tmp[0][1];
			DEL(pa[top[x]],n+1);
		}
		int az=dfn[x]|(1<<K);
		M[az]=Matrix(val(x,0),val(x,1),val(x,0),0);
		while(az>>=1)pushup(az);
		if(pa[top[x]]){
			Matrix tmp=query(dfn[top[x]],mx[top[x]]);
			f[n+1][0]=tmp[0][0],f[n+1][1]=tmp[0][1];
			INS(pa[top[x]],n+1);
		}
		x=pa[top[x]];
	}
}
void LETIN(int x){
	if(cov[x]++)return;
	++zero[x][0];
	change(x);
}
void LETOUT(int x){
	if(--cov[x])return;
	--zero[x][0];
	change(x);
}
int GetAns(void){
	Matrix tmp=query(dfn[1],mx[1]);
	return mo(tmp[0][0]+tmp[0][1]);
}
int main(){
	int m;read(n),read(m);
	for(int i=1;i<=m;++i){
		int u,v;
		read(u),read(v);
		qwq(u,v);qwq(v,u);
	}
	K=0;while(n+1>=(1<<K))++K;
	dfs(1,0);dfs0(1);dfs1(top[1]=1);
	for(int i=(1<<K)-1;i>=1;--i)pushup(i);
	int U=(1<<cnt),ans=GetAns();
	for(int sta=1;sta<U;++sta){
		int pre=((sta-1)^((sta-1)>>1)),now=(sta^(sta>>1));
		int tp=(pre^now),pos=0;while(tp)++pos,tp>>=1;
		if((pre&now)==pre){
			LETIN(S[pos]);LETIN(T[pos]);
		}
		else{
			LETOUT(S[pos]);LETOUT(T[pos]);
		}
		if(sta&1)ans=mo(mod-GetAns()+ans);
		else ans=mo(ans+GetAns());
	}
	write(ans),pc('\n');
	return 0;
}

[AHOI2018/HNOI2018]游戏：

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define ch() getchar()
#define pc(x) putchar(x)
using namespace std;
template<typename T>void read(T&x){
	static char c;static int f;
	for(c=ch(),f=1;c<'0'||c>'9';c=ch())if(c=='-')f=-f;
	for(x=0;c>='0'&&c<='9';c=ch())x=x*10+(c&15);x*=f;
}
template<typename T>void write(T x){
	static char q[65];int cnt=0;
	if(x<0)pc('-'),x=-x;
	q[++cnt]=x%10,x/=10;
	while(x)
		q[++cnt]=x%10,x/=10;
	while(cnt)pc(q[cnt--]+'0');
}
const int maxn=1000005;
int n,lock[maxn],id[maxn],L[maxn],R[maxn],vis[maxn];
void solve(int x){
	if(vis[x])return;vis[x]=true;
	while("Imakf ak ioi"){
		int ok=false;
		if(L[x]>1&&lock[L[x]-1]>=L[x]&&lock[L[x]-1]<=R[x]){
			ok=true;solve(id[L[x]-1]);L[x]=L[id[L[x]-1]];
		}
		if(R[x]<n&&lock[R[x]]>=L[x]&&lock[R[x]]<=R[x]){
			ok=true;solve(id[R[x]+1]);R[x]=R[id[R[x]+1]];
		}
		if(!ok)break;
	}
}
int main(){
	int m,p;
	read(n),read(m),read(p);
	for(int i=1;i<=m;++i){
		int x,y;
		read(x),read(y);
		lock[x]=y;
	}
	id[1]=1;L[1]=R[1]=1;
	for(int i=2;i<=n;++i)
		if(!lock[i-1])R[id[i]=id[i-1]]=i;
		else L[id[i]=i]=R[i]=i;
	for(int i=1;i<=n;++i)solve(id[i]);
	while(p--){
		int s,t;read(s),read(t);
		puts(L[id[s]]<=t&&t<=R[id[s]]?"YES":"NO");
	}
	return 0;
}

[AHOI2018/HNOI2018]排列：

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define ch() getchar()
#define pc(x) putchar(x)
using namespace std;
template<typename T>void read(T&x){
	static char c;static int f;
	for(c=ch(),f=1;c<'0'||c>'9';c=ch())if(c=='-')f=-f;
	for(x=0;c>='0'&&c<='9';c=ch())x=x*10+(c&15);x*=f;
}
template<typename T>void write(T x){
	static char q[65];int cnt=0;
	if(x<0)pc('-'),x=-x;
	q[++cnt]=x%10,x/=10;
	while(x)
		q[++cnt]=x%10,x/=10;
	while(cnt)pc(q[cnt--]+'0');
}
const int maxn=500005;
struct Longlong{
	long long up,dn;
	Longlong(long long up=0,long long dn=1):
		up(up),dn(dn){}
};
bool operator < (const Longlong A,const Longlong B){
	return A.up*B.dn<B.up*A.dn;
}
struct Node{
	Longlong val;int id;
	Node(Longlong val=Longlong(),int id=0):
		val(val),id(id){}
	bool operator < (const Node o)const{
		return val<o.val;
	}
}hp[maxn*2];
int SZ;
void push(Node x){
	int no=++SZ;
	while(no>1&&x<hp[no>>1])
		hp[no]=hp[no>>1],no>>=1;
	hp[no]=x;
}
void pop(void){
	Node x=hp[SZ--];
	int no=1,nt=2;
	while(nt<=SZ){
		if((nt|1)<=SZ&&hp[nt|1]<hp[nt])nt|=1;
		if(hp[nt]<x)hp[no]=hp[nt],no=nt,nt=no<<1;
		else break;
	}
	hp[no]=x;
}
int pa[maxn],sz[maxn];
int Ac(int x){
	return pa[x]==x?x:pa[x]=Ac(pa[x]);
}
int fa[maxn];
long long sm[maxn];
int main(){
	int n;read(n);
	for(int i=1;i<=n;++i)
		read(fa[i]);
	for(int i=1;i<=n;++i){
		sz[pa[i]=i]=1;read(sm[i]);
		push(Node(Longlong(sm[i]),i));
	}
	sz[0]=1;
	long long ans=0;int ok=true;
	while(SZ){
		Node tmp=hp[1];pop();int u=tmp.id;
		if(!u||Ac(u)!=u)continue;int fu=Ac(fa[u]);
		if(fu==u){ok=false;break;}ans+=sm[u]*sz[fu];pa[u]=fu;
		push(Node(Longlong(sm[fu]+=sm[u],sz[fu]+=sz[u]),fu));
	}
	if(!ok)puts("-1");else write(ans),pc('\n');
	return 0;
}

[AHOI2018/HNOI2018]道路：

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
#define ch() getchar()
#define pc(x) putchar(x)
template<typename T>inline void read(T&x){
	int f;char c;
	for(f=1,c=ch();c<'0'||c>'9';c=ch())if(c=='-')f=-f;
	for(x=0;c<='9'&&c>='0';c=ch())x=x*10+(c&15);x*=f;
}
template<typename T>inline void write(T x){
	static char q[64];int cnt=0;
	if(!x)pc('0');if(x<0)pc('-'),x=-x;
	while(x)q[cnt++]=x%10+'0',x/=10;
	while(cnt--)pc(q[cnt]);
}
const int maxn=20005;
int n,son[maxn][2],a[maxn],b[maxn],c[maxn];
long long dp[maxn][45][45];
long long solve(int no,int v0,int v1){
	if(no>=n)return 1ll*c[no-n]*(a[no-n]+v0)*(b[no-n]+v1);
	if(~dp[no][v0][v1])return dp[no][v0][v1];
	return dp[no][v0][v1]=min(solve(son[no][0],v0,v1)+solve(son[no][1],v0,v1+1),
							  solve(son[no][0],v0+1,v1)+solve(son[no][1],v0,v1));
}
int main(){
	read(n);
	for(int i=1;i<n;++i){
		int s,t;read(s),read(t);
		if(s<0)s=n-s-1;if(t<0)t=n-t-1;
		son[i][0]=s,son[i][1]=t;
	}
	for(int i=0;i<n;++i)
		read(a[i]),read(b[i]),read(c[i]);
	memset(dp,-1,sizeof dp);
	write(solve(1,0,0)),pc('\n');
	return 0;
}
posted @ 2021-01-18 20:38  xiaolilsq  阅读(158)  评论(0)  编辑  收藏  举报