CF1435 游记
CF1435 游记
第一次 AK div2 ,我流下了感动的泪水。
Atcoder 掉分没有关系,攒完 RP 之后 CF 就可以上分了。/xyx

A Finding Sasuke
题意简述
给定 \(n\) 个数 \(a_1,a_2,\dots,a_n\) ,其中 \(n\) 是偶数,请找到一组 \(b_1,b_2,\dots,b_n\) 满足 \(\sum_{i=1}^na_ib_i=0\) , \(T\) 组数据。
\(1\le T\le 1000,2\le n\le 100,|a_i|\le 100,a_i\ne 0\) ,你需要保证 \(|b_i|\le 100,b_i\ne 0\) 。
解题思路
显然, \(-a_2,a_1,-a_4,a_3,-a_6,a_5\dots,-a_n,a_{n-1}\) 就满足条件。
参考代码
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
#define ch() getchar()
#define pc(x) putchar(x)
template<typename T>inline void read(T&x){
int f;char c;
for(f=1,c=ch();c<'0'||c>'9';c=ch())if(c=='-')f=-f;
for(x=0;c<='9'&&c>='0';c=ch())x=x*10+(c&15);x*=f;
}
template<typename T>inline void write(T x){
static char q[64];int cnt=0;
if(!x)pc('0');if(x<0)pc('-'),x=-x;
while(x)q[cnt++]=x%10+'0',x/=10;
while(cnt--)pc(q[cnt]);
}
int a[105];
int main(){
int T;read(T);
while(T--){
int n;read(n);
for(int i=1;i<=n;++i)
read(a[i]);
for(int i=1;i<=n;i+=2)
write(-a[i+1]),pc(' '),write(a[i]),pc(" \n"[i==n-1]);
}
return 0;
}
B A New Technique
题意简述
有一个 \(n\times m\) 的矩阵,其中填写的数字为 \(1,2,\dots,n\times m\) ,将每一行打乱顺序和每一列打乱顺序后告诉你,还原原矩阵,保证有解, \(t\) 组数据。
\(1\le t\le 10^5,1\le n,m\le 500,\sum n\times m\le 2.5\times 10^5\) 。
题目分析
相当于告诉你每个数上面是什么,下面是什么,左边是什么,右边是什么,于是就可以做了。
参考代码
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
#define ch() getchar()
#define pc(x) putchar(x)
template<typename T>inline void read(T&x){
int f;char c;
for(f=1,c=ch();c<'0'||c>'9';c=ch())if(c=='-')f=-f;
for(x=0;c<='9'&&c>='0';c=ch())x=x*10+(c&15);x*=f;
}
template<typename T>inline void write(T x){
static char q[64];int cnt=0;
if(!x)pc('0');if(x<0)pc('-'),x=-x;
while(x)q[cnt++]=x%10+'0',x/=10;
while(cnt--)pc(q[cnt]);
}
const int maxn=250005;
int Right[maxn],Left[maxn],Up[maxn],Down[maxn];
int main(){
int T;read(T);
while(T--){
int n,m;
read(n),read(m);
for(int i=1;i<=n*m;++i)
Right[i]=Left[i]=Up[i]=Down[i]=0;
int tot=0;
for(int i=1;i<=n;++i){
int last=0;
for(int j=1;j<=m;++j){
int a;read(a);if(j!=1)Right[last]=a,Left[a]=last;last=a;
}
}
for(int j=1;j<=m;++j){
int last=0;
for(int i=1;i<=n;++i){
int a;read(a);if(i!=1)Down[last]=a,Up[a]=last;last=a;
}
}
int rt;
for(int i=1;i<=n*m;++i){
if(!Up[i]&&!Left[i]){
rt=i;break;
}
}
while(rt){
for(int i=rt;i>=1&&i<=n*m;i=Right[i])
write(i),pc(" \n"[!Right[i]]);
rt=Down[rt];
}
}
return 0;
}
C Perform Easily
题意简述
给定六个数 \(a_1,a_2,\dots,a_6\) 和 \(n\) 个数 \(b_1,b_2,\dots,b_n\) ,请找到一个序列 \(c_1,c_2,\dots,c_n\) ,满足 \(1\le c_i\le 6,a_{c_i}<b_i\) ,并最小化 \(\max(a_{c_i}-b_i)-\min(a_{c_i}-b_i)\) 。
\(1\le a_i,b_i\le 10^9,1\le n\le 10^5\) 。
题目分析
先对于任意的 \(1\le i\le n\) ,求出满足条件的 \(a_{c_i}-b_i\) 的所有可能,考虑枚举 \(\min(a_{c_i}-b_i)\) ,这样的话就是要最小化 \(a_{c_i}-b_i\) ,用一个桶记一下就行了。
参考代码
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
#define ch() getchar()
#define pc(x) putchar(x)
template<typename T>inline void read(T&x){
int f;char c;
for(f=1,c=ch();c<'0'||c>'9';c=ch())if(c=='-')f=-f;
for(x=0;c<='9'&&c>='0';c=ch())x=x*10+(c&15);x*=f;
}
template<typename T>inline void write(T x){
static char q[64];int cnt=0;
if(!x)pc('0');if(x<0)pc('-'),x=-x;
while(x)q[cnt++]=x%10+'0',x/=10;
while(cnt--)pc(q[cnt]);
}
const int maxn=100005;
int sum[maxn][6],a[6],cnt[maxn];
struct Temp{
int id,val;
Temp(int id=0,int val=0):
id(id),val(val){}
bool operator < (const Temp o)const{
return val<o.val;
}
}all[maxn*6];
int now[maxn];
int main(){
for(int i=0;i<6;++i)
read(a[i]);
sort(a,a+6);
int n,ac=0,mx=0;read(n);
for(int i=0;i<n;++i){
int b;read(b);int cn=0;
for(int j=5;j>=0;--j)if(b>a[j]){
all[ac++]=Temp(i,sum[i][cn++]=b-a[j]);
}
cnt[i]=cn;mx=max(mx,sum[i][now[i]=0]);
}
sort(all,all+ac);int ans=0x3f3f3f3f;
for(int l=0,r=0;l<ac;l=r=r+1){
int val=all[l].val;
while(r+1<ac&&all[r+1].val==val)++r;
ans=min(ans,mx-val);int ok=true;
for(int i=l;i<=r&&ok;++i){
int id=all[i].id;++now[id];
if(now[id]>=cnt[id])ok=false;
else mx=max(mx,sum[id][now[id]]);
}
if(!ok)break;
}
write(ans),pc('\n');
return 0;
}
D Shurikens
题意简述
给定 \(n\) ,有一个长度为 \(n\) 的排列 \(a\) ,有 \(2n\) 次操作和一个初始为空的小根堆和一个初始为 \(0\) 的数字 \(c\) ,每次操作要么是令 \(c\gets c+1\) ,然后将 \(a_c\) 插入堆中,要么是删除小根堆的堆顶,现在给出操作序列和每次删除掉的数字,询问是否存在一个满足条件的排列 \(a\) ,如果存在需要构造出来。
\(1\le n\le 10^5\) 。
题目分析
每次找到被删掉的最小值,然后找到它前面第一个操作,如果是插入操作就删除这个插入操作和这个删除操作,否则就无解,证明显然。
参考代码
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
#define ch() getchar()
#define pc(x) putchar(x)
template<typename T>inline void read(T&x){
int f;char c;
for(f=1,c=ch();c<'0'||c>'9';c=ch())if(c=='-')f=-f;
for(x=0;c<='9'&&c>='0';c=ch())x=x*10+(c&15);x*=f;
}
template<typename T>inline void write(T x){
static char q[64];int cnt=0;
if(!x)pc('0');if(x<0)pc('-'),x=-x;
while(x)q[cnt++]=x%10+'0',x/=10;
while(cnt--)pc(q[cnt]);
}
const int maxn=100005,saxn=maxn*2;
struct Temp{
int id,val;
Temp(int id=0,int val=0):
id(id),val(val){}
bool operator < (const Temp o)const{
return val<o.val;
}
}sum[maxn];
int id[saxn],pa[saxn];
int ac(int x){
return pa[x]==x?x:pa[x]=ac(pa[x]);
}
int ans[maxn];
int main(){
int n;read(n);int n2=n*2,cnt=0,an=0;
for(int i=1;i<=n2;++i){
char c=ch();
while(c!='+'&&c!='-')c=ch();
if(c=='-'){
int a;read(a);
sum[++an]=Temp(i,a);
}
else{
id[i]=++cnt;
}
pa[i]=i;
}
pa[0]=0;
sort(sum+1,sum+an+1);
for(int i=1;i<=an;++i){
int no=sum[i].id,val=sum[i].val;
int to=ac(no-1);
if(!id[to])return puts("NO"),0;
ans[id[to]]=val;
pa[no]=pa[to]=to-1;
}
puts("YES");
for(int i=1;i<=n;++i)
write(ans[i]),pc(" \n"[i==n]);
return 0;
}
E Solo mid Oracle
题意简述
给定 \(a,b,c,d\) ,有一个敌人,你可以对他发动技能来伤害他,每次发动技能时该敌人会瞬间失去 \(a\) 滴血,然后在接下来的 \(c\) 秒内,他每秒会恢复 \(b\) 滴血,恢复血量可以叠加,如果你在第 \(i,j(i<j)\) 秒都发动了技能,那么需要满足 \(j\ge i+d\) ,当这个敌人在某一秒的时候的血量小于等于 0 ,那么他就死了,询问你可以杀死的血量最高的敌人的血量是多少,如果可以杀死任意血量的敌人,输出 -1 , \(t\) 组询问。
\(1\le t\le 10^5,1\le a,b,c,d\le 10^6\) 。
题目分析
感觉细节挺多的一道题目。
首先贪心地想,技能肯定是能放就放,所以放技能大概就是:
现在要求的就是前缀和的最小值。
先考虑判 -1 ,随着秒数的增加,一直到第一个技能的治愈效果消失的时候,每次伤害就变成固定的了,此时上面的矩阵大概长这样:
可以把这些数分成若干块,使得每一块的值都相等:
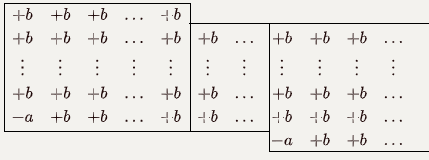
(这张图中每一块代表的就是最左边的矩形和中间的矩形的并)
如果每一块的值都是负数,那么显然 -1 ,其他情况不可能 -1 。
上图中最左边的 -a 是第 \(\lfloor\frac{c}{d}\rfloor\) 个 -a ,第 \(i\) 个 -a 的位置是 \((i-1)\times d+1\) ,所以这个 -a 的位置就是 \(s=(\lfloor\frac{c}{d}\rfloor-1)\times d+1\) ,第一个 -a 的治愈效果会一直执行到 \(c+1\) 这个位置,由此可以得出,最左边的矩形的权值和就是 \(((c+1-s+1)\times \lfloor\frac{c}{d}\rfloor-1)\times b-a\) ;最左边的 -a 的右边的第一个 -a 的位置就是 \(s+d\) ,所以中间的矩形的权值和就是 \((s+d-(c+2))\times (\lfloor\frac{c}{d}\rfloor-1)\times b\) 。所以如果下面这个式子的值为负数,那么答案就是 -1 :
如果不是负数,说明这个总的矩阵的前缀和的最小值一定在第一个 -a 到第 \(\lfloor\frac{c}{d}\rfloor\) 个 -a 之间,并且这一列必然是一次放技能的开始,因为往后面走不会更优了,确定了选择区间之后,我们发现第一个 -a 的治愈效果一定会到达当前选择的位置,所以考虑问题就更加简单了。
第 \(x\) 个 -a 造成的共伤害是多少?枚举前面 \(x-1\) 个 -a 造成的治愈效果,总伤害应该是 \(-a\times x+\sum_{y=1}^{x-1}((x-y)\times d\times b)\) ,即 \(-a\times x+\frac{x(x-1)}{2}\times d\times b\) ,是个二次函数,可以直接求对称轴,也可以三分,我用的方法是三分。
参考代码
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
#define ch() getchar()
#define pc(x) putchar(x)
template<typename T>inline void read(T&x){
int f;char c;
for(f=1,c=ch();c<'0'||c>'9';c=ch())if(c=='-')f=-f;
for(x=0;c<='9'&&c>='0';c=ch())x=x*10+(c&15);x*=f;
}
template<typename T>inline void write(T x){
static char q[64];int cnt=0;
if(!x)pc('0');if(x<0)pc('-'),x=-x;
while(x)q[cnt++]=x%10+'0',x/=10;
while(cnt--)pc(q[cnt]);
}
long long a,b,c,d;
long long f(long long x){
return x*(x-1)/2*d*b-a*x;
}
int main(){
int T;read(T);
while(T--){
read(a),read(b),read(c),read(d);
long long e=c/d+1,pos=(e-1)*d+1;
long long eb=(e*(c+1-pos+1)-1)*b+(pos+d-(c+2))*(e-1)*b;
if(eb<a)puts("-1");
else{
long long l=1,r=e,ans=0;
while(l+3<r){
long long ml=(l+r)>>1,mr=ml+1;
if(f(ml)>f(mr))ans=min(ans,f(l=ml));
else ans=min(ans,f(r=mr));
}
while(l<=r)ans=min(ans,f(l++));
write(-ans),pc('\n');
}
}
return 0;
}
总结
这次比赛状态还不错, E 这种神仙细节题目也没有挂,希望下次也要保持这样的状态。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号