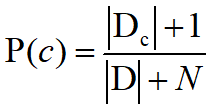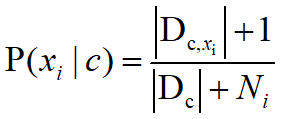《机器学习(周志华)》笔记--贝叶斯分类器（2）--朴素贝叶斯分类器：先验概率、后验概率、条件概率、朴素贝叶斯表达式、拉普拉斯平滑

二、朴素贝叶斯分类器

1、相关三概率

　　给定 N 个类别，设随机样本向量x={x₁,x₂,…,x_d} ，相关的三个概率：

　　（1）先验概率P(c) ：根据以前的知识和经验得出的c类样本出现的概率，与现在无关。

　　（2）后验概率P(c|x) ：相对于先验概率而言，表示x 属于c类的概率。

　　（3）条件概率P(x|c) ：已知属于c类的样本中发生x的概率。

2、朴素贝叶斯表达式

 　　贝叶斯公式：

　　　　　　

 　　贝叶斯决策：

　　　　　　

　　朴素的贝叶斯分类器：假设所有的属性都相互独立。基于属性条件独立性假设，P(c|x) 可写作：

 　　　　　　

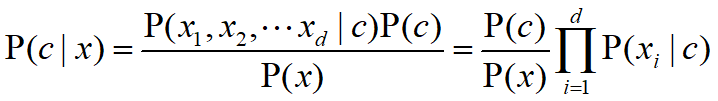
　　可得出朴素贝叶斯分类器的表达式：

 　　　　　　

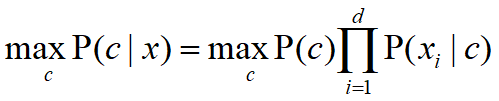
 　　先验概率：

　　　　　　

　　条件概率：

　　　　　　

 　　例：

　　　　　　　　

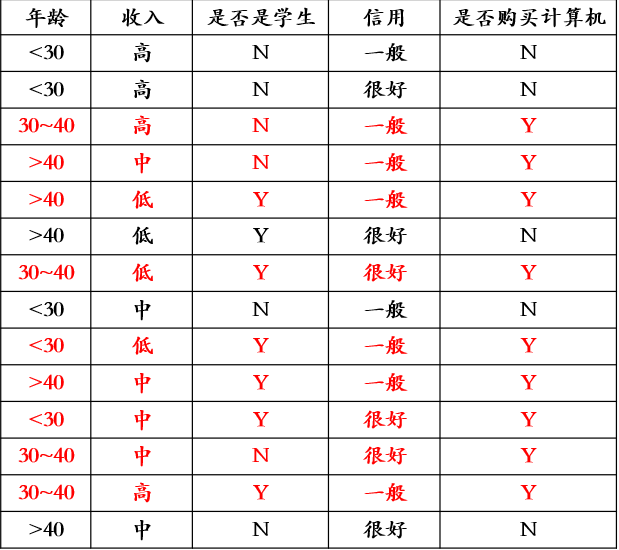
　　　　一个销售顾客的数据库如右表所示，利用贝叶斯法则预测，符合下列条件的人员购买计算机的可能性x=（年龄<30,收入=中,学生否=Y,信用=一般)。

　　解：

　　　　假定C₁={购买计算机},C₂={不购买计算机},

　　　　先验概率：

　　　　　　　　P(C1)=9/14=0.643,

                   　　   P (C2)=5/14=0.357,

　　　　条件概率：

　　　　　　　　P(年龄<30|C₁)=2/9,      　　P(年龄<30|C₂)=3/5

　　　　　　　　P(收入=中|C₁)=4/9,        　  P(收入=中|C₂)=2/5

　　　　　　　　P(学生否=Y|C₁)=6/9,           P(学生否=Y|C₂)=1/5

　　　　　　　　P(信用=一般|C₁)=6/9,          P(信用=一般|C₂)=2/5

　　　　因此

　　　　　　　 P(x|C₁)=(2/9)*(4/9)*(6/9)*(6/9)=0.044

        　　　　    P(x|C₂)=(3/5)*(2/5)*(1/5)*(2/5)=0.019

　　　　最后计算：

　　　　　　P(x|C₁)*P(C₁) =0.044*0.643=0.028

                      P(x|C₂)*P(C₂)=0.019*0.357=0.007

　　　　因为P(x|C₁)*P(C₁)>P(x|C₂)*P(C₂) ，顾客x购买计算机的可能性比较大。

 3、拉普拉斯平滑　

　　拉普拉斯平滑：为了避免其他属性携带的信息被其他未出现过的属性值“抹去”，在估计概率值时通常要进行平滑。具体的说，令N表示训练集D中的类别数，N_i表示第i个属性可能的取值数，则：