《机器学习(周志华)》笔记--贝叶斯分类器（1）--贝叶斯决策：条件概率、联合概率、全概率、贝叶斯公式

一、贝叶斯决策

　　贝叶斯决策论是概率框架下实施决策的基本方法，对分类任务来说，在所有相关概率已知的理想情形下，贝叶斯考虑如何基于这些概率和误判损失来选择最优的类别标记。

      朴素贝叶斯分类算法是基于贝叶斯定理与特征条件独立假设的分类方法。

1、条件概率

　　概率指的是某一事件A发生的可能性，表示为P(A)。

　　条件概率指的是某一事件A已经发生了条件下，另一事件B发生的可能性，表示为P(B|A)。

　　　　今天有25%的可能性下雨，即P(下雨)=0.25;

　　　　今天75%的可能性是晴天，即P(晴天)=0.75;

　　　　如果下雨，我有75%的可能性穿外套，即P(穿外套|下雨)=0.75;

　　　　如果下雨，我有25%的可能性穿T恤，即P(穿T恤|下雨)=0.25;

　　从上述例子可以看出，条件概率描述的是|右边的事件已经发生之后，左边的事件发生的可能性，而不是两个事件同时发生的可能性！

2、联合概率

　　设A，B是两个事件，且P(A)>0，则

　　　　P(B|A)=P(AB)/P(A)

　　联合概率：两个事件同时发生的概率

　　　　P(AB)=P(B|A)*P(A)

　　　　当A、B独立时：P(AB)=P(A)*P(B)

　　例：

　　　　现在有一批产品共100件，次品有10件，从中不放回地抽取2次，每次取1件。计算第一次为次品，第二次为正品的概率。

　　解：

　　　　假设事件A为第一次为次品，事件B为第二次为正品。则P(AB)=P(A)*P(B|A)=(10/100)*(90/99)=0.091

3、全概率

　　全概率就是表示达到某个目的，有多种方式（或者造成某种结果，有多种原因），问达到目的的概率是多少（造成这种结果的概率是多少）

　　若事件B₁ ,B₂,…,B_n 两两互不相容，并且其概率和为1。那么对于任意一个事件A都满足：

　　　　　　

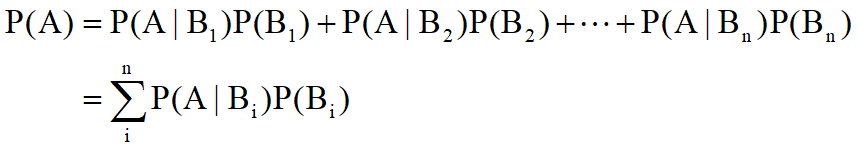
 　　例：

　　　　小明从家到学校有三条路：L1、L2、L3，选择每条路的概率分别为：0.5，0.3，0.2，每条路通畅的概率分别为：0.2，0.4，0.7。　　

　　　   计算小明不迟到（不拥堵就不会迟到）的概率。

　　解：

　　　　A，B1，B2，B3分别表示小明没有迟到，小明选择道路L1，道路L2，道路L3，则

　　　　P(A)=P(AB₁)+P(AB₂)+P(AB₃)

       　　 　　=P(A|B₁)*P(B₁)+P(A|B₂)*P(B₂)+P(A|B₃)*P(B₃)

       　　 　　=0.2*0.5+0.4*0.3+0.7*0.2=0.36

 4、贝叶斯公式

 　　贝叶斯公式：已知事件已经发生了，计算引发该事件的各种原因的概率。

　　　　　　　　　　　

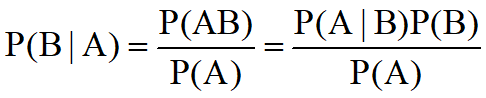
　　例：

　　　　设某工厂有甲、乙、丙三个车间生产同一种产品，已知各车间的产量分别占全厂产量的25%，35%，40%，而且各车间的次品率分别为5%，4%，2%，现从待出厂的产品中检查出一个次品，试判断它是由甲车间生产的概率。

　　解：

　　　　A表示产品为次品，B₁，B₂，B₃表示产品由甲、乙、丙三个车间生产，求P(B₁|A)

　　　　P(A|B₁)*P(B₁)=0.05*0.25=0.0125

　　　　P(A)=P(A|B₁)*P(B₁)+P(A|B₂)*P(B₂)+P(A|B₃)*P(B₃)

      　　　　  =0.05*0.25+0.04*0.35+0.02*0.4=0.0345

　　　　P(B₁|A)=P(A|B₁)*P(B₁)/P(A)=0.362