《机器学习(周志华)》笔记--支持向量机（4）--序列最小优化算法：smo算法基本思想、SMO算法目标函数的优化、SMO算法代码实现

四、序列最小优化算法（smo算法）

1、smo算法基本思想

　　支持向量机的学习问题可以形式化为求解凸二次规划问题。 这样的凸二次规划问题具有全局最优解， 并且有许多最优化算法可以用于这一问题的求解。 但是当训练样本容量很大时， 这些算法往往变得非常低效， 以致无法使用。 所以，如何高效地实现支持向量机学习就成为一个重要的问题。

　　目前人们已提出许多快速实现算法。其中最具代表的就是序列最小最优化算法（sequential minimaloptimization，smo）。

　　smo算法要解如下凸二次规划的对偶问题：

　　　　　　

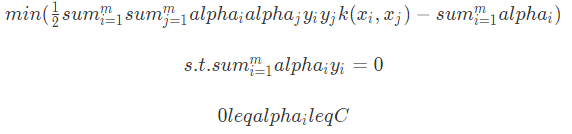
 　　算法是一种启发式算法， 其基本思路是：如果所有变量的解都满足此最优化问题的KKT条件，那么这个最优化问题的解就得到了。因为KKT条件是该最优化问题的充分必要条件。否则,选择两个变量，固定其他变量，针对这两个变量构建一个二次规划问题。这个二次规划问题关于这两个变量的解应该更接近原始二次规划问题的解，因为这会使得原始二次规划问题的目标函数值变得更小。重要的是，这时子问题可以通过解析方法求解，这样就可以大大提高整个算法的计算速度。子问题有两个变量,一个是违反KKT条件最严重的那一个，另一个由约束条件自动确定。如此，smo算法将原问题不断分解为子问题并对子问题求解，进而达到求解原问题的目的。具体如下：

　　选择两个变量 alpha1​ , alpha2​，其它变量 alphai​ , i = 3 , 4 , .. m是固定的。

　　于是，smo的最优化问题的子问题可以写成：

　　　　　　

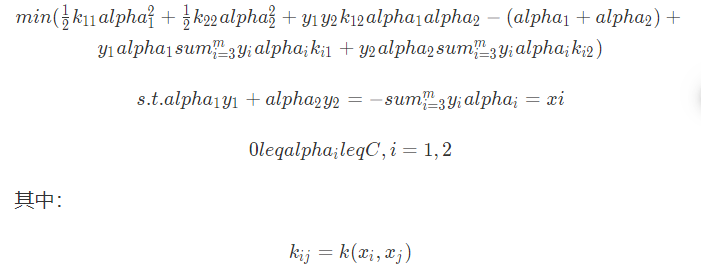
 2、SMO算法目标函数的优化

　　为了求解上面含有这两个变量的目标优化问题，我们首先分析约束条件，所有的 alpha1​ , alpha2​ 都要满足约束条件，然后在约束条件下求最小。

　　　　　　

 　　　　　　

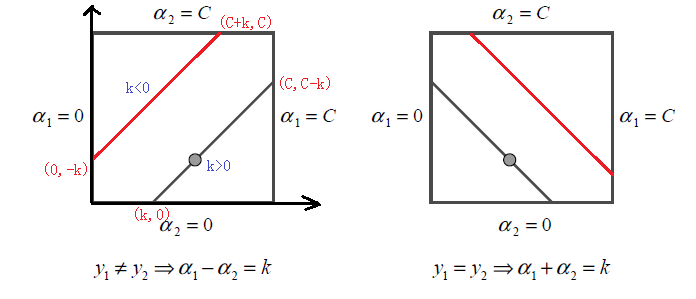
 3、SMO算法代码实现

 （1）数据集介绍

　　数据集共包括400个样本，有年龄跟工资两个特征，标签为是否购买房产，1表示购买，0表示未购买。我们取300个样本作为训练集，100个样本作为测试集。部分数据如下：

　　　　　　　　

 （2）获取数据代码

#获取数据
import pandas as pd
dataset = pd.read_csv('./step3/Social_Network_Ads.csv')
x = dataset.iloc[:, [2, 3]].values
x = x.astype(float)
y = dataset.iloc[:, 4].values
#将0替换为-1
for i in range(len(y)):
    if y[i]==0:
        y[i]=-1
from sklearn.model_selection import  train_test_split
train_data, test_data, train_label, test_label = train_test_split(x, y, test_size = 0.25, random_state = 61)
#特征标准化
from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
train_data = sc.fit_transform(train_data)
test_data = sc.transform(test_data)

  （3）整体代码

#encoding=utf8
import numpy as np
class smo:
    def __init__(self, max_iter=100, kernel='linear'):
        '''
        input:max_iter(int):最大训练轮数
              kernel(str):核函数，等于'linear'表示线性，等于'poly'表示多项式
        '''
        self.max_iter = max_iter
        self._kernel = kernel
    #初始化模型
    def init_args(self, features, labels):
        self.m, self.n = features.shape
        self.X = features
        self.Y = labels
        self.b = 0.0
        # 将Ei保存在一个列表里
        self.alpha = np.ones(self.m)
        self.E = [self._E(i) for i in range(self.m)]
        # 错误惩罚参数
        self.C = 1.0
   
    #kkt条件    
    def _KKT(self, i):
        y_g = self._g(i)*self.Y[i]
        if self.alpha[i] == 0:
            return y_g >= 1
        elif 0 < self.alpha[i] < self.C:
            return y_g == 1
        else:
            return y_g <= 1

    # g(x)预测值，输入xi（X[i]）
    def _g(self, i):
        r = self.b
        for j in range(self.m):
            r += self.alpha[j]*self.Y[j]*self.kernel(self.X[i], self.X[j])
        return r

    # 核函数,多项式添加二次项即可
    def kernel(self, x1, x2):
        if self._kernel == 'linear':
            return sum([x1[k]*x2[k] for k in range(self.n)])
        elif self._kernel == 'poly':
            return (sum([x1[k]*x2[k] for k in range(self.n)]) + 1)**2    
        return 0

    # E（x）为g(x)对输入x的预测值和y的差
    def _E(self, i):
        return self._g(i) - self.Y[i]

    #初始alpha
    def _init_alpha(self):
        # 外层循环首先遍历所有满足0<a<C的样本点，检验是否满足KKT
        index_list = [i for i in range(self.m) if 0 < self.alpha[i] < self.C]
        # 否则遍历整个训练集
        non_satisfy_list = [i for i in range(self.m) if i not in index_list]
        index_list.extend(non_satisfy_list)
        for i in index_list:
            if self._KKT(i):
                continue
            E1 = self.E[i]
            # 如果E2是+，选择最小的；如果E2是负的，选择最大的
            if E1 >= 0:
                j = min(range(self.m), key=lambda x: self.E[x])
            else:
                j = max(range(self.m), key=lambda x: self.E[x])
            return i, j

    #选择alpha参数   
    def _compare(self, _alpha, L, H):
        if _alpha > H:
            return H
        elif _alpha < L:
            return L
        else:
            return _alpha

    #训练
    def fit(self, features, labels):
        '''
        input:features(ndarray):特征
              label(ndarray):标签
        '''
        self.init_args(features, labels)
        for t in range(self.max_iter):
            i1, i2 = self._init_alpha()
            # 边界
            if self.Y[i1] == self.Y[i2]:
                L = max(0, self.alpha[i1]+self.alpha[i2]-self.C)
                H = min(self.C, self.alpha[i1]+self.alpha[i2])
            else:
                L = max(0, self.alpha[i2]-self.alpha[i1])
                H = min(self.C, self.C+self.alpha[i2]-self.alpha[i1])
            E1 = self.E[i1]
            E2 = self.E[i2]
            # eta=K11+K22-2K12
            eta = self.kernel(self.X[i1], self.X[i1]) + self.kernel(self.X[i2], self.X[i2]) - 2*self.kernel(self.X[i1], self.X[i2])
            if eta <= 0:
                continue
            alpha2_new_unc = self.alpha[i2] + self.Y[i2] * (E2 - E1) / eta
            alpha2_new = self._compare(alpha2_new_unc, L, H)
            alpha1_new = self.alpha[i1] + self.Y[i1] * self.Y[i2] * (self.alpha[i2] - alpha2_new)
            b1_new = -E1 - self.Y[i1] * self.kernel(self.X[i1], self.X[i1]) * (alpha1_new-self.alpha[i1]) - self.Y[i2] * self.kernel(self.X[i2], self.X[i1]) * (alpha2_new-self.alpha[i2])+ self.b 
            b2_new = -E2 - self.Y[i1] * self.kernel(self.X[i1], self.X[i2]) * (alpha1_new-self.alpha[i1]) - self.Y[i2] * self.kernel(self.X[i2], self.X[i2]) * (alpha2_new-self.alpha[i2])+ self.b 
            if 0 < alpha1_new < self.C:
                b_new = b1_new
            elif 0 < alpha2_new < self.C:
                b_new = b2_new
            else:
                # 选择中点
                b_new = (b1_new + b2_new) / 2
            # 更新参数
            self.alpha[i1] = alpha1_new
            self.alpha[i2] = alpha2_new
            self.b = b_new
            self.E[i1] = self._E(i1)
            self.E[i2] = self._E(i2)     

      
    def predict(self, data):
        '''
        input:data(ndarray):单个样本
        output:预测为正样本返回+1，负样本返回-1
        '''
        r = self.b
        for i in range(self.m):
            r += self.alpha[i] * self.Y[i] * self.kernel(data, self.X[i])
        return 1 if r > 0 else -1