《机器学习(周志华)》笔记--支持向量机（3）--核函数：核技巧、核函数计算过程、特殊映射函数

三、核函数

　1、核技巧　

　　若不存在一个能正确划分两类样本的超平面, 怎么办 ?

　　数学上可以证明，如果原始空间是有限维，即属性数有限，则一定存在一个高维特征空间使样本可分。将样本从原始空间映射到一个更高维的特征空间 , 使样本在这个特征空间内线性可分。

　　我们的数据集有时候是非线性可分的情况，如下图：

　　　　　　　　

 　　对于非线性的情况，SVM 的处理方式就是选择一个核函数。简而言之：在线性不可分的情况下，SVM 通过某种事先选择的非线性映射（核函数）将输入变量映到一个高维特征空间，将其变成在高维空间线性可分，在这个高维空间中构造最优分类超平面。如将本关上图数据集映射成如下情况：

　　　　　　　　　　　　

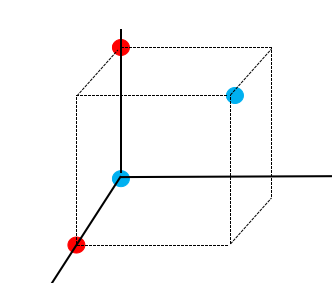
　2、核函数计算

　　　　　　

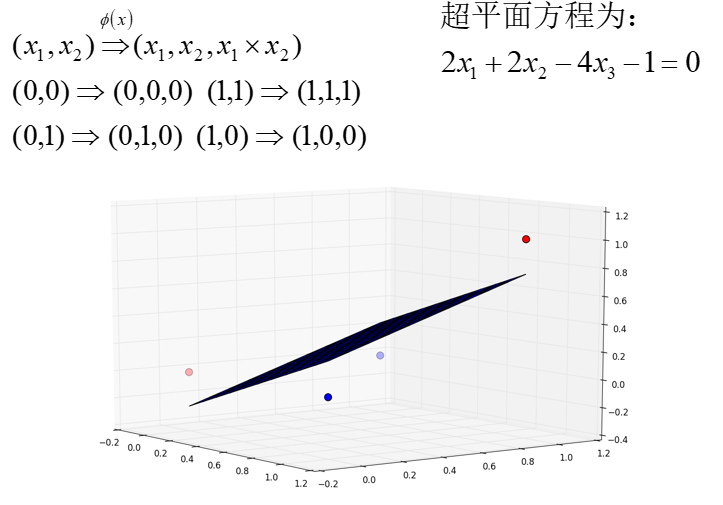
　　这里涉及到两个样本在特征空间内的内积，由于特征空间的维数可能很高，甚至无穷维，直接计算通常是困难的，为了避开这个障碍，我们可以设想这样一个函数。

 　　　　　　

　　任意两个样本的核函数值构成的矩阵，任何一个核函数都隐式的定义了一个特征空间，当样本线性不可分时，我们需要将样本映射到高维空间内，但我们不知道哪个核函数合适，因此说核函数的选择成为决定支持向量机性能的关键。

　　　　　　　　

　　基本经验：文本数据常用线性核，情况不明时可先尝试高斯核。