《机器学习(周志华)》笔记--支持向量机（1）--间隔与支持向量：线性二分类问题、支持向量机基本思想、间隔与支持向量、间隔与支持向量数学推导、支持向量机基本型

　　支持向量机 (Support Vector Machine) 是由Vapnik等人于1995年提出来的，之后随着统计理论的发展，支持向量机 SVM 也逐渐受到了各领域研究者的关注，在很短的时间就得到了很广泛的应用。支持向量机是被公认的比较优秀的分类模型。同时，在支持向量机的发展过程中，其理论方面的研究得到了同步的发展，为支持向量机的研究提供了强有力的理论支撑。

一、间隔与支持向量

1、线性二分类问题

　　线性二分类问题其本质上就是找到一条决策边界，将我们的数据分成两类。如下图：

　　　　　　

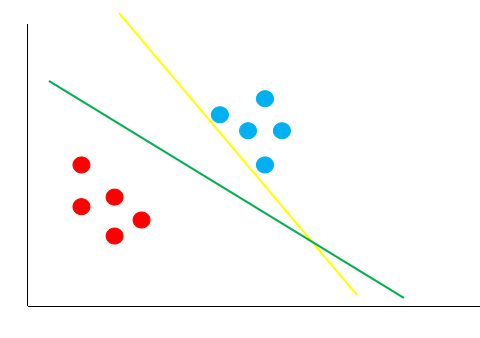
　　图中的绿线与黄线都能很好的将图中的红点与蓝点给区分开。但是，哪条线的泛化性更好呢？（泛化性也就是说，我们的这条直线，不仅需要在训练集(已知的数据)上能够很好的将红点跟蓝点区分开来，还要在测试集(未知的数据)上将红点跟蓝点给区分开来。）

　　假如经过训练，我们得到了黄色的这条决策边界用来区分我们的数据，这个时候又来了一个数据，即黑色的点，那么你觉得黑色的点是属于红的这一类，还是蓝色的这一类呢？

 　　　　　　

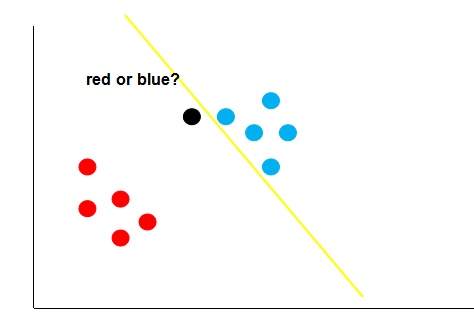
　　如上图，根据黄线的划分标准，黑色的点应该属于红色这一类。可是，我们肉眼很容易发现，黑点离蓝色的点更近，它应该是属于蓝色的点。这就说明，黄色的这条直线它的泛化性并不好，它对于未知的数据并不能很好的进行分类。那么，如何得到一条泛化性好的直线呢？这个就是支持向量机考虑的问题。

2、支持向量机基本思想

　　支持向量机的思想认为，一条决策边界它如果要有很好的泛化性，它需要满足一下以下两个条件：

　　　　（1）能够很好的将样本划分


　　　　（2）离最近的样本点最远

　　比如下图中的黑线：

　　　　　　

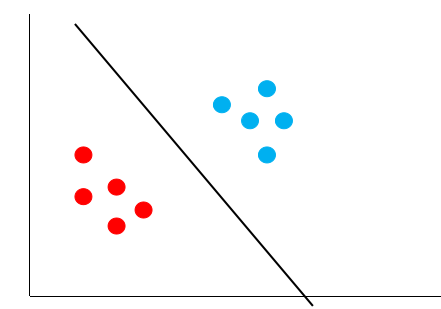
 　　它能够正确的将红点跟蓝点区分开来，而且，它还保证了对未知样本的容错率，因为它离最近的红点跟蓝点都很远，这个时候，再来一个数据，就不会出现之前黄色决策边界的错误了。

　　　　　　

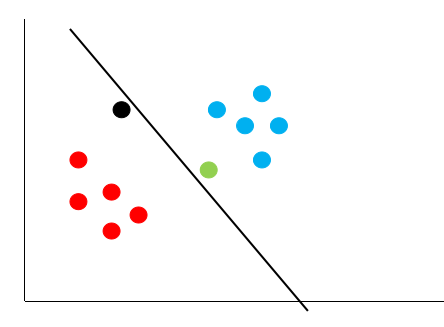
 　　无论新的数据出现在哪个位置，黑色的决策边界都能够很好的给它进行分类，这个就是支持向量机的基本思想。

3、间隔与支持向量

　　　　　　　

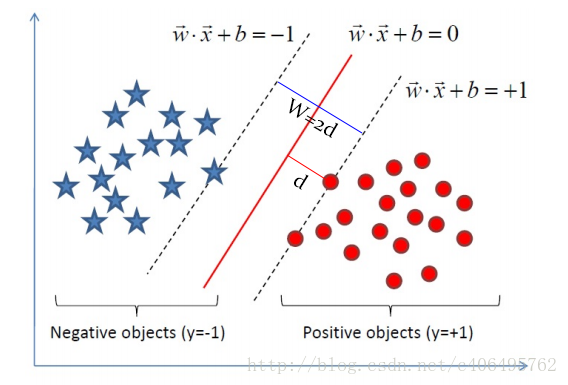
　　 支持向量:距离超平面最近的样本点；

　　间隔：两个异类支持向量到超平面的距离之和。

　　支持向量机就是要寻找具有最大间隔的超平面。

　　在样本空间中，决策边界可以通过如下线性方程来描述：

　　　　　　　　　　　　

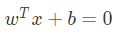
 　　其中 w = ( w1​ , w2 ​, .. , wd ​) 为法向量，决定了决策边界的方向。b 为位移项，决定了决策边界与原点之间的距离。

　　显然，决策边界可被法向量和位移确定，我们将其表示为（w , b）。样本空间中的任意一个点x,到决策边界（w , b）的距离可写为：

　　　　　　　　　　　　 

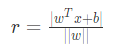
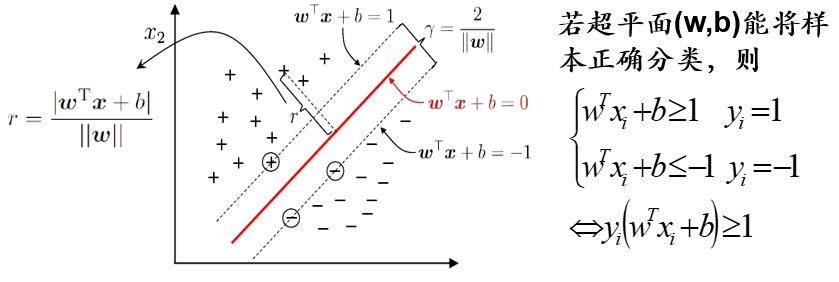
　　假设决策边界（w , b）能够将训练样本正确分类，即对于任何一个样本点 (xi ​, yi​) ,若它为正类，即 yi ​= +1 时， ；若它为负类，即 yi ​= −1时， 。

 　　　　

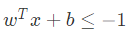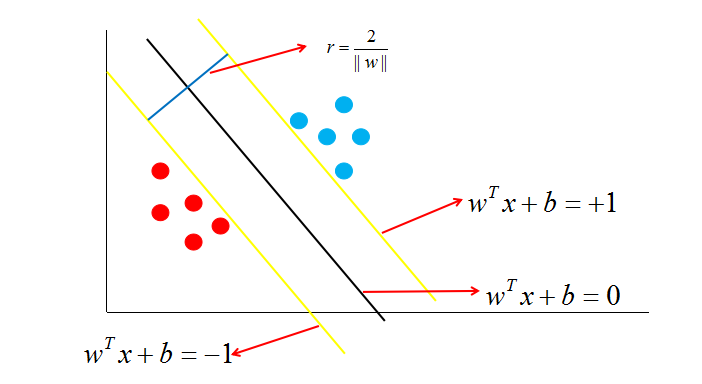
　　如图中，距离最近的几个点使两个不等式的等号成立，它们就被称为支持向量，即图中两条黄色的线。两个异类支持向量到超平面的距离之和为： 。它被称为间隔，即蓝线的长度。

　　欲找到具有“最大间隔”的决策边界，即黑色的线，也就是要找到能够同时满足如下式子的  w 与  b :

　　　　　　

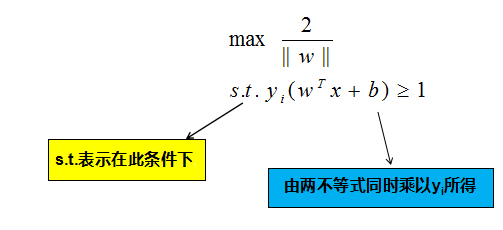
 4、间隔与支持向量数学推导

　　　　

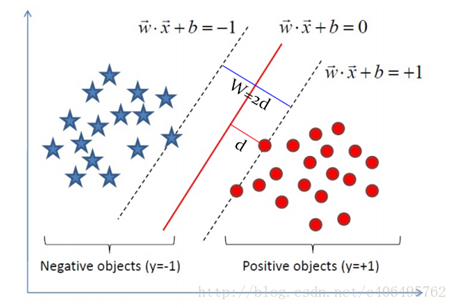
 推导过程：

　　　　　　　　

　　　　　　　　

　　　　　　　　

　　　　　　　　

实例计算：　

　　假设下面使两类中的一些点集：

　　　　　　

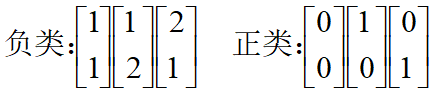
　　划分它们并找到最优分类线。支持向量是什么？间隔是是什么？

 解得：

　　　　   

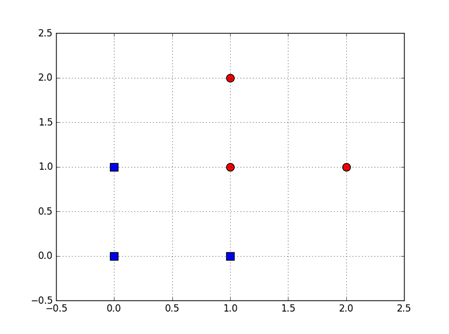
5、支持向量机基本型