《机器学习(周志华)》笔记--神经网络（3）--感知机与多层网络：感知机与逻辑操作、多层前馈神经网络

二、感知机与多层网络

3、感知机与逻辑操作

（1）线性模型

　　感知机只有输出层神经元进行激活函数处理，即只拥有一层功能神经元，其学习能力十分有限。有些逻辑运算（与、或、非问题）可以看成线性可分任务。若两类模式是线性可分的，即存在一个线性超平面能将它们分开，则感知机的学习过程一定会收敛而求得适当的权向量w；否则感知机学习过程会发生振荡，w难以稳定下来，不能求得合适的解。

　　利用感知机可以实现一些逻辑操作，也就是我们可以为感知机找到一组权值和阈值，实现操作。

　　　　1）逻辑或

　　　　  

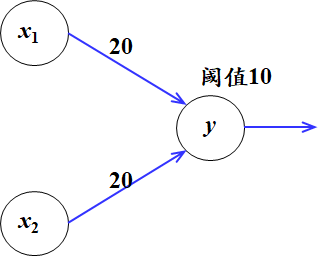
　　　　2）逻辑与

　　　　

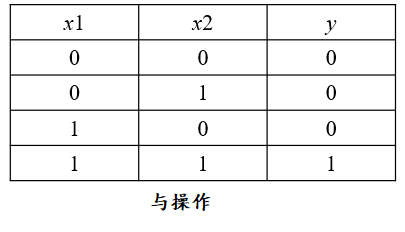
　　　　3）与非操作

　　　　

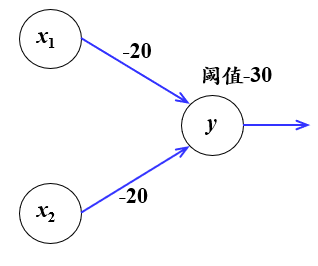
（2）非线性模型　

　　感知机是线性模型，对于线性可分的任务能够找到分类边界，但对于线性不可分的任务，需考虑多层功能神经元。

　　异或运算可以通过其他逻辑运算实现。单个神经元智能实现线性任务，将多个神经元进行堆叠就可以实现非线性任务。输出层和输入层之间的一层神经元，被称为隐层或隐含层，隐含层和输出层神经元都是拥有激活函数的功能神经元。

  

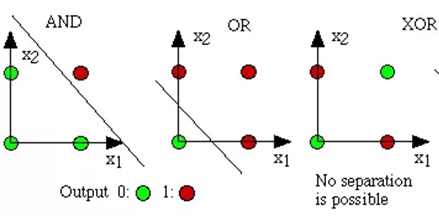
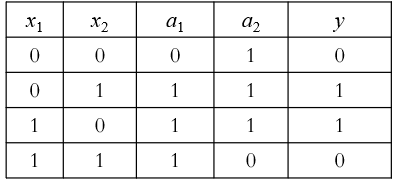
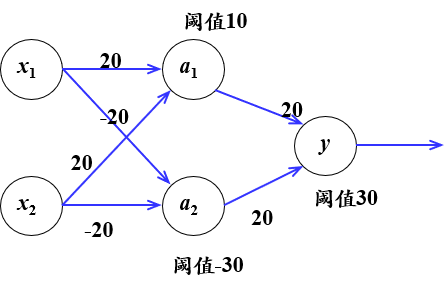
　　也就是说，若将三个神经元进行叠加，便能够解决异或问题。在上图中，输出层和输出层之间的一层神经元，被称为隐层或隐含层。

感知机与逻辑运算代码实现：

#逻辑与
import numpy as np
import matplotlib.pyplot as plt
X0 = np.array([[0,0],
              [0,1],
              [1,0]])
X1 = np.array([[1,1]])
ones = -np.ones((X0.shape[0],1))
X0 = np.hstack((ones,X0))
ones = -np.ones((X1.shape[0],1))
X1 = np.hstack((ones,X1))
X = np.vstack((-X0,X1))
W = np.ones((X.shape[1],1))
flag = True
while(flag):
    flag = False
    for i in range(len(X)):
        x = X[i,:].reshape(-1,1)    
        if np.dot(W.T,x)<=0:
            W = W + x
            flag = True
plt.grid()
plt.scatter(X0[:,1],X0[:,2],c = 'r',marker='o',s=500)
plt.scatter(X1[:,1],X1[:,2],c = 'g',marker='*',s=500)
p1=[0,1]
p2=[(W[0]-p1[0]*W[1])/W[2],(W[0]-p1[1]*W[1])/W[2]]
plt.plot(p1,p2)
plt.show()
print(W)

#逻辑或非
import numpy as np
import matplotlib.pyplot as plt
X1 = np.array([[0,0]])
X0 = np.array([[0,1],
               [1,0],
               [1,1]])
ones = -np.ones((X0.shape[0],1))
X0 = np.hstack((ones,X0))
ones = -np.ones((X1.shape[0],1))
X1 = np.hstack((ones,X1))
X = np.vstack((-X0,X1))
Y = np.array([[0],[0],[0],[0],[1],[1],[1],[1]])
W = np.ones((X.shape[1],1))
flag = True
while(flag):
    flag = False
    for i in range(len(X)):
        x = X[i,:].reshape(-1,1)    
        if np.dot(W.T,x)<=0:
            W = W + x
            flag = True
plt.grid()
plt.scatter(X0[:,1],X0[:,2],c = 'r',marker='o',s=500)
plt.scatter(X1[:,1],X1[:,2],c = 'g',marker='*',s=500)
p1=[0,1]
p2=[(W[0]-p1[0]*W[1])/W[2],(W[0]-p1[1]*W[1])/W[2]]
plt.plot(p1,p2)
plt.show()
print(W)

#逻辑或
import numpy as np
import matplotlib.pyplot as plt
X0 = np.array([[0,0]])
X1 = np.array([[0,1],
               [1,0],
               [1,1]])
ones = -np.ones((X0.shape[0],1))
X0 = np.hstack((ones,X0))
ones = -np.ones((X1.shape[0],1))
X1 = np.hstack((ones,X1))
X = np.vstack((-X0,X1))
Y = np.array([[0],[0],[0],[0],[1],[1],[1],[1]])
W = np.ones((X.shape[1],1))
flag = True
while(flag):
    flag = False
    for i in range(len(X)):
        x = X[i,:].reshape(-1,1)    
        if np.dot(W.T,x)<=0:
            W = W + x
            flag = True
plt.grid()
plt.scatter(X0[:,1],X0[:,2],c = 'r',marker='o',s=500)
plt.scatter(X1[:,1],X1[:,2],c = 'g',marker='*',s=500)
p1=[0,1]
p2=[(W[0]-p1[0]*W[1])/W[2],(W[0]-p1[1]*W[1])/W[2]]
plt.plot(p1,p2)
plt.show()
print(W)

#异或
import numpy as np
import matplotlib.pyplot as plt
X0 = np.array([[0,0],
               [1,1]])
X1 = np.array([[0,1],
               [1,0]])

plt.grid()
plt.scatter(X0[:,0],X0[:,1],c = 'r',marker='o',s=500)
plt.scatter(X1[:,0],X1[:,1],c = 'g',marker='*',s=500)
plt.show()

4、多层前馈神经网络

　　更一般的，常见的神经网络是形如下图的层级结构，由输入层，隐藏层，输出层构成。

　　特点：每层神经元与下层神经元完全互连，神经元之间不存在同层连接，也不存在跨层连接。

　　这样网络也称为前馈神经网络。

　　　　　　

　　当隐藏层只有一层时，该网络为两层神经网络，由于输入层未做任何变换，可以不看做单独的一层。实际中，网络输入层的每个神经元代表了一个特征，输出层个数代表了分类标签的个数（在做二分类时，如果采用sigmoid分类器，输出层的神经元个数为1个；如果采用softmax分类器，输出层神经元个数为2个），而隐藏层层数以及隐藏层神经元是由人工设定。

　　神经网络的学习过程，就是根据训练数据来调整神经元之间的连接权以及每个功能神经元的阈值，换言之，神经网络学到的东西，蕴涵在连接权和阈值中。