《机器学习(周志华)》笔记--决策树（5）--轴平行划分：单变量决策树、多变量决策树

七、多变量决策树

 1、从“树”到“规则”

　　一棵决策树对应于一个“规则集”，每个从根结点到叶结点的分支路径对应于一条规则。

举例：

　　　　　　

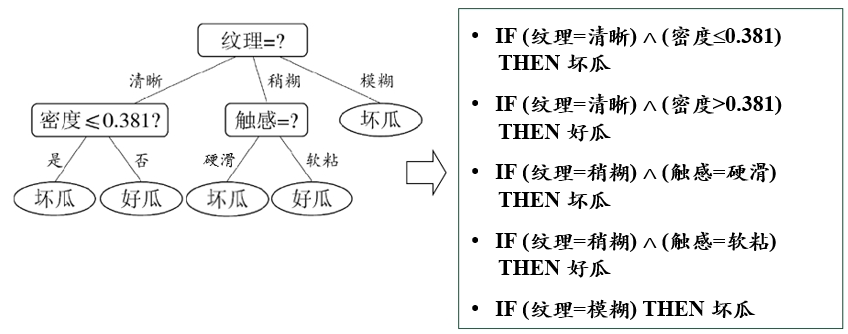
　　好处：

　　　　（1）改善可理解性

　　　　（2）进一步提升泛化能力（ 由于转化过程中通常会进行前件合并、泛化等操作，C4.5Rule 的泛化能力通常优于 C4.5决策树）

2、轴平行划分

　　若我们把每个属性视为坐标空间中的一个坐标轴，则 d 个属性描述的样本就对应了 d 维空间中的一个数据点，对样本分类则意味着在这个坐标空间中寻找不同类样本之间的分类边界，决策树所形成的决策边界有一个明显的特点：轴平行（axis-parallel），即它的分类边界由若干个与坐标轴平行的分段组成。

（1）单变量决策树

　　单变量决策树：在每个非叶结点仅考虑一个划分属性，产生“轴平行”分类面，寻找分类边界。

举例：

　　　　

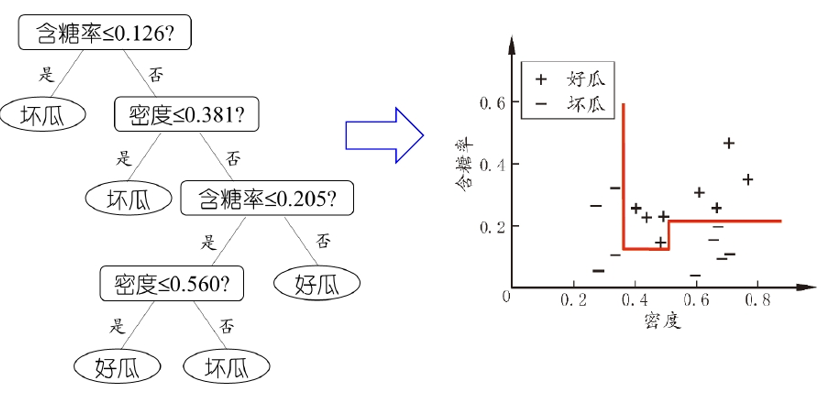
　　当学习任务所对应的分类边界很复杂时，需要非常多段划分才能获得较好的近似。

　　　　　　

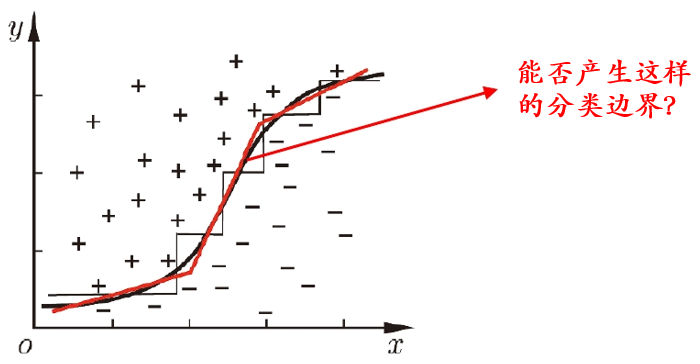
　　若能使用斜的划分模型，则决策树模型就会大大简化。这就引入了“多变量决策树”。

（2）多变量决策树

　　多变量决策树：每个非叶结点不仅考虑一个属性，例如“斜决策树” (oblique decision tree) 不是为每个非叶结点寻找最优划分属性，而是建立一个线性分类器。

举例：

　　

　　更复杂的“混合决策树”甚至可以在结点嵌入神经网络或其他非线性模型。