《机器学习(周志华)》笔记--决策树（4）--连续与缺失值：连续值处理、缺失值处理
六、连续与缺失值
1、连续值处理
到目前为止我们仅讨论了基于离散属性来生成决策树，现实学习任务中常常遇到连续属性，有必要讨论如何在决策树学习中使用连续属性。我们将相邻的两个属性值的平均值作为候选点。
基本思路：连续属性离散化。
常见做法：二分法（这正是C4.5决策树算法中采用的机制）。
对于连续属性a，我们可考察包括 n-1 个元素的候选划分集合（n 个属性值可形成 n-1 个候选点）：
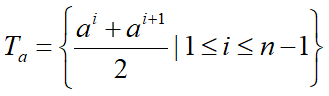
利用每个候选点对数据进行划分，得到两个子集，计算信息增益，取最大的信息增益对应作为该属性的信息增益。
举例：
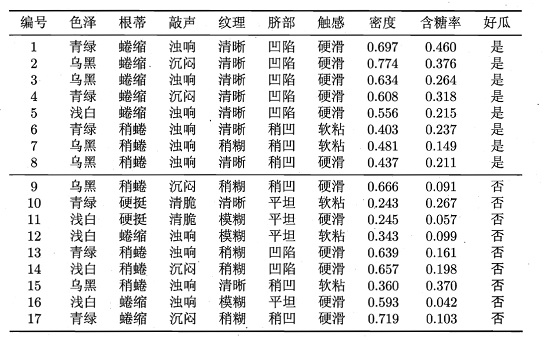
对于数据集中的属性“密度”，在决策树开始学习时，根节点包含的17个训练样本在该属性上取值均不同。该属性的候选划分点集合包括16个候选值：
T密度 = {0.244，0.294，0.351，0.381，0.42.，0.459，0.518，0.574，0.600，0.621，0.636，0.648，0.661，0.681，0.708，0.746}
计算可知属性“密度”信息增益为0.262，对应划分点0.381.
对属性“含糖率”，其候选划分点集合也包括16个候选值：
T含糖率 = {0.049，0.074，0.095，0.101，0.126，0.155，0.179，0.204，0.213，0.226，0.250，0.265，0.292，0.344，0.373，0.418}
计算可知其信息增益为0.349，对应于划分点0.126.
类似的，计算得到的各属性的信息增益值：
比较能够知道纹理的信息增益值最大，因此，“纹理”被选作根节点划分属性，下面只要重复上述过程递归的进行，就能构造出一颗决策树：
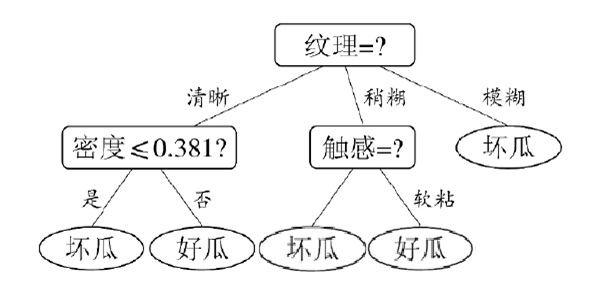
有一点需要注意的是：与离散属性不同，若当前结点划分属性为连续属性，该属性还可作为其后代结点的划分属性。
到目前为止我们仅讨论了基于离散属性来生成决策树，现实学习任务中常常遇到连续属性，有必要讨论如何在决策树学习中使用连续属性。对于连续的属性，后续进行划分属性的时候还可以继续使用。
2、缺失值处理
现实任务中常会遇到不完整样本，即样本的某些属性值缺失。如果简单地放弃不连续样本，仅使用无缺值样本来进行学习，显然是对数据信息极大的浪费。显然我们有必要考虑利用有缺失属性值的训练样例来进行学习。
在决策树中处理含有缺失值的样本的时候，需要解决两个问题：
- 如何在属性值缺失的情况下进行划分属性的选择？（比如“色泽”这个属性有的样本在该属性上的值是缺失的，那么该如何计算“色泽”的信息增益？）
- 给定划分属性，若样本在该属性上的值是缺失的，那么该如何对这个样本进行划分？（即到底把这个样本划分到哪个结点里？）
以上简单介绍了决策树在训练阶段是如何处理有缺失值的样本的，若测试样本属性也有缺失值，则：
- 如果有专门处理缺失值的分支，就走这个分支。
- 用这篇论文提到的方法来确定属性a的最有可能取值，然后走相应的分支。
- 从属性a最常用的分支走
- 同时探查所有的分支，并组合他们的结果来得到类别对应的概率，（取概率最大的类别）
- 将最有可能的类别赋给该样本。
C4.5中采用的方法是：测试样本在该属性值上有缺失值，那么就同时探查（计算）所有分支，然后算每个类别的概率，取概率最大的类别赋值给该样本。
