《机器学习(周志华)》笔记--线性模型(5)--逻辑回归实现二分类、LogisticRegression、多分类学习、纠错输出码(ECOC)
四、逻辑回归
6、逻辑回归实现二分类
(1)对于每个样本x利用线性回归模型得到输出z:
![]()
(2)将线性回归模型的输出z利用sigmoid函数得到概率:
![]()
(3)构造损失函数:
![]()
(4)损失函数关于向量W=( w0 , ... , wd )的函数,求损失函数的梯度:
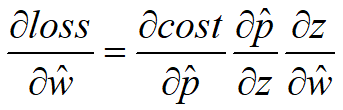
由于: ![]()
所以:![]()
由于:![]()
所以: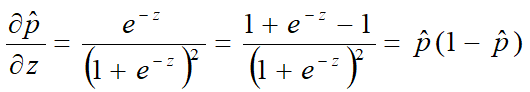
由于:![]() ,
,![]()
所以: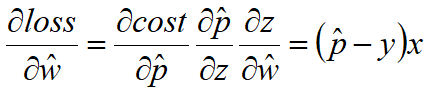
![]()
写成矩阵的形式:
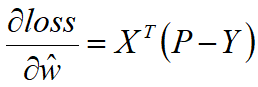
其中X为m×(d+1)的样本矩阵,Y为m维的样本类别矩阵,P为m维的概率矩阵。
利用梯度下降修改参数ŵ:
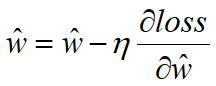
(5)代码实现
#===========1、逻辑回归模拟=========== import numpy as np import pandas as pd import matplotlib.pyplot as plt #************sigmoid函数计算********* def sigmoid(z): return 1/(1+np.exp(-z)) #***********利用迭代方法求最优的w******* def mymodel(X,Y,eta,W,iters): i=1 while (i<=iters): err = sigmoid(np.dot(X,W))-Y gradient = np.dot(X.T,err) W=W-eta*gradient i=i+1 return W #***********读取数据******************* df = pd.read_csv('ex1.csv',header=None) data = df.values X = data[:,:-1] Y = data[:,-1].reshape((-1,1)) #**********构造增广矩阵**************** ones = np.ones((X.shape[0],1)) X = np.hstack((ones,X)) #*********模型初始化****************** W = np.ones((X.shape[1],1)) eta = 0.001 #*********调用模型,求最优解********** W = mymodel(X,Y,eta,W,500) #*********绘制正例和负例************* xcord1 = []; ycord1 = [] xcord2 = []; ycord2 = [] for i in range(X.shape[0]): if int(Y[i])==1: xcord1.append(X[i,1]) ycord1.append(X[i,2]) else: xcord2.append(X[i,1]) ycord2.append(X[i,2]) plt.scatter(xcord1,ycord1,s = 20, c = 'red', marker = 's',alpha=.5) plt.scatter(xcord2, ycord2, s = 20, c = 'green',alpha=.5) #*********绘制决策边界************ x_w = np.linspace(-3,3,100) y_w = (-W[0]-W[1]*x_w)/W[2] print(W) plt.plot(x_w,y_w,c='blue') plt.show()
LogisticRegression
LogisticRegression中默认实现了 OVR ,因此LogisticRegression可以实现多分类。
LogisticRegression的构造函数中有三个常用的参数可以设置:
-
solver:{'newton-cg' , 'lbfgs', 'liblinear', 'sag', 'saga'}, 分别为几种优化算法。默认为liblinear; -
C:正则化系数的倒数,默认为 1.0 ,越小代表正则化越强; -
max_iter:最大训练轮数,默认为 100 。
和sklearn中其他分类器一样,LogisticRegression类中的fit函数用于训练模型,fit函数有两个向量输入:
-
X:大小为 [样本数量,特征数量] 的ndarray,存放训练样本; -
Y:值为整型,大小为 [样本数量] 的ndarray,存放训练样本的分类标签。
LogisticRegression类中的predict函数用于预测,返回预测标签,predict函数有一个向量输入:
X:大小为[样本数量,特征数量]的ndarray,存放预测样本。
LogisticRegression的使用代码如下:
logreg = LogisticRegression(solver='lbfgs',max_iter =10,C=10) logreg.fit(X_train, Y_train) result = logreg.predict(X_test)
#=======2、利用sklearn中logisticregression函数========= import pandas as pd from sklearn.model_selection import train_test_split from sklearn.linear_model import LogisticRegression from sklearn.metrics import accuracy_score,precision_score,recall_score,f1_score,\ roc_auc_score,confusion_matrix,classification_report filename = 'pima_data.csv' names = ['preg','plas','blood','skin','insulin','bmi','pedi','age','class'] data = pd.read_csv(filename,names=names) array = data.values X=array[:,:-1] Y=array[:,-1] test_size = 0.3 seed = 4 X_train,X_test,Y_train,Y_test = train_test_split(X,Y,test_size=test_size,random_state=seed) model = LogisticRegression() model.fit(X_train,Y_train) y_predict = model.predict(X_test) y_proba = model.predict_proba(X_test)[:,1] y_true = Y_test print(accuracy_score(y_true,y_predict)) print(y_proba) print(y_predict)
7、多分类学习
拆解法:将一个多分类任务拆分为若干个二分类任务求解。
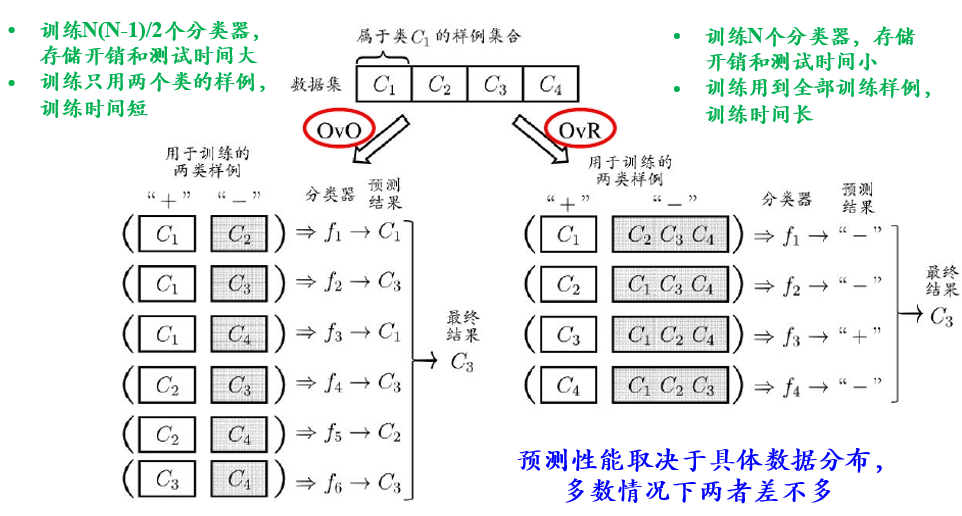
8、纠错输出码(ECOC)
多对多(Many vs Many, MvM): 将若干类作为正类,若干类作为反类。
一种常见方法:纠错输出码 (Error Correcting Output Code)
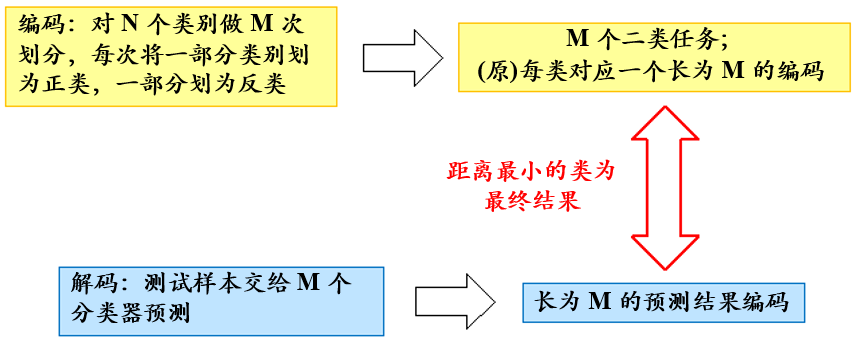
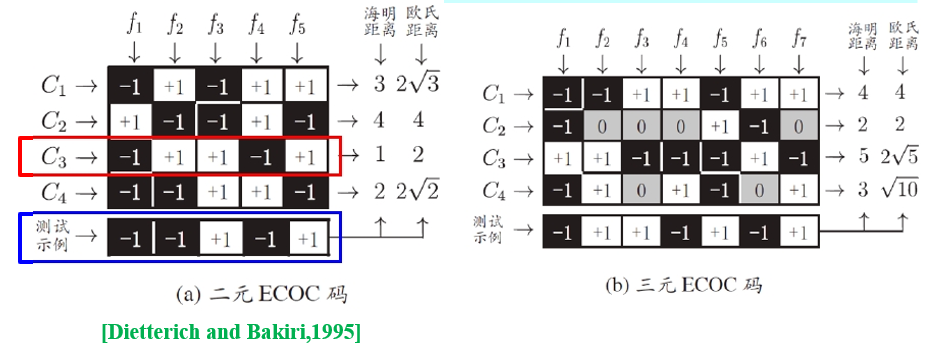
ECOC编码对分类器错误有一定容忍和修正能力,编码越长、纠错能力越强。
对同等长度的编码,理论上来说,任意两个类别之间的编码距离越远,则纠错能力越强。
根据多个分类器的分类结果综合判断,其中一个分类器出错不会影响全局判断,编码越长,纠错能力越强。编码不同的位数。


