《机器学习(周志华)》笔记--线性模型（4）--梯度解释、梯度下降法算法思想、算法原理、算法流程、代码实现

四、逻辑回归

5、梯度下降法

（1）梯度解释

　　偏导数：简单来说是对于一个多元函数，选定一个自变量并让其他自变量保持不变，只考察因变量与选定自变量的变化关系。

　　梯度：梯度的本意是一个向量，由函数对每个参数的偏导组成，表示某一函数在该点处的方向导数沿着该方向取得最大值，即函数在该点处沿着该方向变化最快，变化率最大。

　　　　　　　　

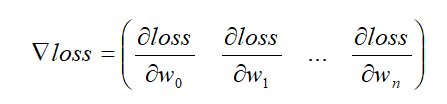
　　梯度向量的方向即为函数值增长最快的方向，沿着梯度方向可以最快地找到函数的最大值，而我们要求误差的最小值，所以在梯度下降中我们要沿着梯度相反的方向：

　　　　　　             　

　　　　其中0<=η<=1为学习率，学习率的大小会对我们的算法产生影响，学习率太小，逼近极值点的速度慢，学习率太大，逼近极值点的速度快，但容易产生震荡。

（2）梯度下降算法思想：

　　梯度下降是一种非常通用的优化算法，能够为大范围的问题找到最优解。

　　梯度下降的中心思想就是迭代地调整参数从而使损失函数最小化。

　　假设你迷失在山上的迷雾中，你能感觉到的只有你脚下路面的坡度。快速到达山脚的一个策略就是沿着最陡的方向下坡，这就是梯度下降的做法。即通过测量参数向量 θ 相关的损失函数的局部梯度，并不断沿着降低梯度的方向调整，直到梯度降为 0 ，达到最小值。

　　梯度下降公式如下：

　 　　　　　　

　　对应到每个权重公式为：

　　　　       

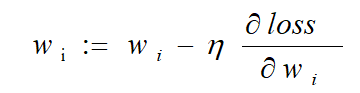
　　　　其中 ，η 为学习率，是 0 到 1 之间的值，是个超参数，需要我们自己来确定大小。

 （3）算法原理：

　　在传统机器学习中，损失函数通常为凸函数，假设此时只有一个参数，则损失函数对参数的梯度即损失函数对参数的导数。

　　①如果刚开始参数初始在最优解的左边，如图 5.3.1 。很明显，这个时候损失函数对参数的导数是小于 0 的，而学习率是一个 0 到 1 之间的数，此时按照公式更新参数，初始的参数减去一个小于 0 的数是变大，也就是在坐标轴上往右走，即朝着最优解的方向走。

　　　　                                          

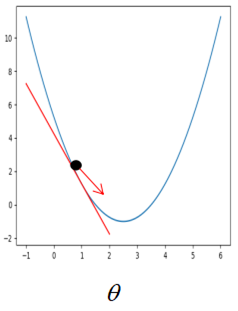
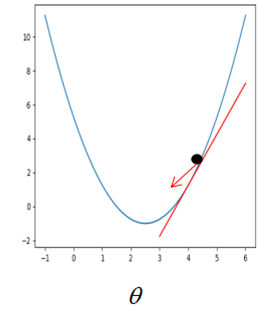
 　　　　　　　　　　　　　　　　图 5.3.1                                                    图5.3.2

　　②如果参数初始在最优解的右边，如图5.3.2。此时按照公式更新，参数将会朝左走，即最优解的方向。

　　所以，不管刚开始参数初始在何位置，按着梯度下降公式不断更新，参数都会朝着最优解的方向走。

（4）梯度下降算法流程　

　　1）随机初始参数

　　2）确定学习率

　　3）求出损失函数对参数梯度

　　4）按照公式更新参数

　　5）重复 3) 4)直到满足终止条件（如：损失函数或参数更新变化值小于某个阈值，或者训练次数达到设定阈值）

（5）代码实现梯度下降

　　要求：使用 Python 实现梯度下降算法，并损失函数最小值时对应的参数theta，theta会返回给外部代码，由外部代码来判断theta是否正确。

# -*- coding: utf-8 -*-
import numpy as np
import warnings
warnings.filterwarnings("ignore")

def gradient_descent(initial_theta,eta=0.05,n_iters=1000,epslion=1e-8):
    '''
    梯度下降
    :param initial_theta: 参数初始值，类型为float
    :param eta: 学习率，类型为float
    :param n_iters: 训练轮数，类型为int
    :param epslion: 容忍误差范围，类型为float
    :return: 训练后得到的参数
    '''
    theta = initial_theta
    i_iter = 0
    while i_iter < n_iters:
        gradient = 2*(theta-3)
        last_theta = theta
        theta = theta - eta*gradient
        if(abs(theta-last_theta)<epslion):
            break
        i_iter +=1
    return theta