《机器学习(周志华)》笔记--线性模型（3）--逻辑回归思想、概率计算、sigmoid 函数、逻辑回归的损失函数计算

四、逻辑回归

　　逻辑回归是属于机器学习里面的监督学习，它是以回归的思想来解决分类问题的一种非常经典的二分类分类器。由于其训练后的参数有较强的可解释性，在诸多领域中，逻辑回归通常用作baseline模型，以方便后期更好的挖掘业务相关信息或提升模型性能。

1、逻辑回归思想

　　当一看到“回归”这两个字，可能会认为逻辑回归是一种解决回归问题的算法，然而逻辑回归是通过回归的思想来解决二分类问题的算法。

　　逻辑回归的基本思想：将样本所属正例的概率作为模型的输出，根据此概率值对样本的类别进行预测：

　　　　                                         

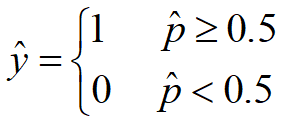
　　解释说明：逻辑回归是将样本特征和样本所属类别的概率联系在一起，假设现在已经训练好了一个逻辑回归的模型为 f(x) ，模型的输出是样本 x 的标签是 1 的概率，则该模型可以表示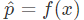。若得到了样本 x 属于标签 1 的概率后，很自然的就能想到当 时 x 属于标签 1 ，否则属于标签 0 。所以就有：

                                                          

　　(其中 ​为样本 x 根据模型预测出的标签结果，标签 0 和标签 1 所代表的含义是根据业务决定的，比如在癌细胞识别中可以使 0 代表良性肿瘤， 1 代表恶性肿瘤)。

　　由于概率是 0 到 1 的实数，所以逻辑回归若只需要计算出样本所属标签的概率就是一种回归算法，若需要计算出样本所属标签，则就是一种二分类算法。

 2、概率计算

　　那么逻辑回归中样本所属标签的概率怎样计算呢？

分析：

　　线性回归输出为的值域是(-∞,+∞)

　　概率的值域是(0,1)

　　关键：找到一个函数σ将线性回归得到的(-∞,+∞)的实数转换成(0,1)的概率值。

　　 逻辑回归中样本所属标签的概率其实和线性回归有关系，学习了线性回归的同学肯定知道线性回归无非就是训练出一组参数和 b 来拟合样本数据，线性回归的输出为。不过的值域是 (−∞,+∞) ，如果能够将值域为 (−∞,+∞) 的实数转换成 (0,1) 的概率值的话问题就解决了。要解决这个问题很自然地就能想到将线性回归的输出作为输入，输入到另一个函数中，这个函数能够进行转换工作，假设函数为 σ ，转换后的概率为 ​，则逻辑回归在预测时可以看成

　　　　　　                     

3、sigmoid 函数

 　     中的σ 其实就是sigmoid函数。

　　sigmoid函数的公式为：

　　　　                 

　　函数曲线：

                 

　　从sigmoid函数的图像可以看出当 t 趋近于 −∞ 时函数值趋近于 0 ，当 t 趋近于 +∞ 时函数值趋近于 1 。可见sigmoid函数的值域是 (0,1) ，满足我们要将 (−∞,+∞) 的实数转换成 (0,1) 的概率值的需求。因此逻辑回归在预测时可以看成：

　　　　　　　　　　　　

4、逻辑回归的损失函数

　　（1）为什么需要损失函数？

　　训练逻辑回归模型的过程其实与之前学习的线性回归一样，就是去寻找合适的  和 b 使得模型的预测结果与真实结果尽可能一致。所以就需要一个函数能够衡量模型拟合程度

的好坏，也就是说当模型拟合误差越大的时候，函数值应该比较大，反之应该比较小，这就是损失函数。

　　（2）逻辑回归的损失函数计算

　　逻辑回归计算出的样本所属类别的概率 ，样本所属类别的判定条件为：

                                                       

 　　很明显，在预测样本属于哪个类别时取决于算出来的 。从另外一个角度来说，假设现在有一个样本的真实类别为1，模型预测样本为类别1的概率为0.9的话，就意味着这个模型

认为当前样本的类别有90%的可能性为1，有10%的可能性为0。所以从这个角度来看，逻辑回归的损失函数与有关。当然逻辑回归的损失函数不仅仅与  有关，它还与真实类别有

关。

　　①假设现在有两种情况：

　　　　情况A：现在有个样本的真实类别是1，模型预测出来该样本是类别1的概率是0.7（也就是说类别0的概率为0.3）；

　　　　情况B：现在有个样本的真实类别是1，模型预测出来该样本是类别1的概率是0.6（也就是说类别0的概率为0.4）；

　　　　问题：AB两种情况哪种情况的误差更大？

　　　　很显然，情况B的误差更大！因为情况A中模型认为样本是类别1的可能性只有70%，而B有60%。

　　　　结论：当真实类别为1时，概率越大，误差越小；

　　②假设现在有两种情况：

　　　　情况A：现在有个样本的真实类别是0，但是模型预测出来该样本是类别1的概率是0.7（也就是说类别0的概率为0.3）；

　　　　情况B：现在有个样本的真实类别是0，但是模型预测出来该样本是类别1的概率是0.6（也就是说类别0的概率为0.4）；

　　　　问题：AB两种情况哪种情况的误差更大？

　　　　很显然，情况A的误差更大！因为情况A中模型认为样本是类别0的可能性只有30%，而B有40%。

　　　　结论：当真实类别为0时，概率越小，误差越小。　

　　逻辑回归的损失函数(对数损失函数)：

　　　　                    

　　当样本的真实类别为1时，上式就变成：

　　　　　　　　    

　　当样本的真实类别为0时，上式就变成：

　　　　　　         

　　             

　　　　　　　　图4.4.1 类别为1                                                                                          图4.4.2  类别为0

　　在一般情况下需要计算的是m条样本数据的平均损失值，所以损失函数的最终形态如下：

　　　　            

　　　　其中，m 表示数据集中样本的数量，i 表示数据集中第 i 个样本：

　　知道了逻辑回归的损失函数之后，逻辑回归的训练流程就很明显了，就是寻找一组合适的W和b，使得损失值最小。找到这组参数后模型就确定下来了。