《机器学习(周志华)》笔记--线性模型(2)--线性回归训练流程、线性回归的正规方程解、LinearRegression模型、线性回归方法用于波士顿房价预测
三、线性回归
5、线性回归训练流程
线性回归模型训练流程如下:
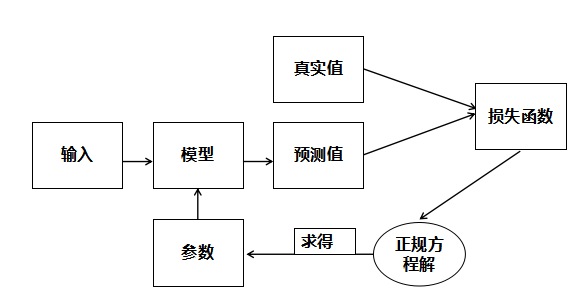
6、线性回归的正规方程解
对线性回归模型,假设训练集中 m个训练样本,每个训练样本中有 n个特征,可以使用矩阵的表示方法,预测函数可以写为:
Y = hetaX
其损失函数可以表示为:
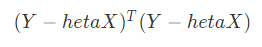
其中,标签 Y 为 mx1 的矩阵,训练特征 X 为 mx(n+1)的矩阵,回归系数 heta为(n+1)x1 的矩阵,对 heta求导,并令其导数等于0,可以得到 ![]()
所以,最优解为:
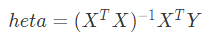
这个就是正规方程解,我们可以通过最优方程解直接求得我们所需要的参数。
7、线性回归模拟
import numpy as np import pandas as pd import matplotlib.pyplot as plt #*************读取某数据集************** df = pd.read_csv("ex0_1.csv",header=None) data = df.values X=data[:,0].reshape((-1,1)) Y=data[:,1].reshape((-1,1)) plt.scatter(X,Y) x_min = min(X) x_max = max(X) #*************构造增广矩阵*************** ones=np.ones((X.shape[0],1)) X=np.hstack((ones,X)) #************结束*********************** #***********求解正规方程解************** XT=X.T XTX=np.dot(XT,X) XTX_1=np.linalg.inv(XTX) XTX_1XT=np.dot(XTX_1,XT) W=np.dot(XTX_1XT,Y) #**********结束********************** #*********绘制拟合的直线************ x_w = np.linspace(x_min,x_max,100) x_w = x_w.reshape((-1,1)) ones = np.ones((x_w.shape[0],1)) x_w = np.hstack((ones,x_w)) y_w = np.dot(x_w,W) plt.plot(x_w[:,1],y_w) plt.show()
8、实例讲解—波斯顿房价预测
(1)数据集介绍
波斯顿房价数据集共有506条波斯顿房价的数据,每条数据包括对指定房屋的13项数值型特征和目标房价组成。用数据集的80%作为训练集,数据集的20%作为测试集,训练集和测试集中都包括特征和目标房价。
sklearn中已经提供了波斯顿房价数据集的相关接口,想要使用该数据集可以使用如下代码:
from sklearn import datasets #加载波斯顿房价数据集 boston = datasets.load_boston() #X表示特征,y表示目标房价 X = boston.data y = boston.target
数据集中部分数据与标签如下图所示:

(2)线性回归训练流程
由数据集可以知道,每一个样本有13个特征与目标房价,而我们要做的事就是通过这13个特征来预测房价,我们可以构建一个多元线性回归模型,来对房价进行预测。模型如下:
y = b + w1x1 + w2x2 + ... + wnxn
其中xi表示第i个特征值,wi表示第i个特征对应的权重,b表示偏置,y表示目标房价。
为了方便,我们稍微将模型进行变换:
y = w0x0 + w1x1 + w2x2 + ... + wnxn
其中x0等于1。
Y = heta.X
heta = ( w0 , w1 , ... , wn )
X = ( 1 , x1 , ... , xn )
而我们的目的就是找出能够正确预测的多元线性回归模型,即找出正确的参数 heta。
那么如何寻找呢?通常在监督学习里面都会使用这么一个套路,构造一个损失函数,用来衡量真实值与预测值之间的差异,然后将问题转化为最优化损失函数。既然损失函数是用来衡量真实值与预测值之间的差异那么很多人自然而然的想到了用所有真实值与预测值的差的绝对值来表示损失函数。不过带绝对值的函数不容易求导,所以采用MSE(均方误差)作为损失函数,公式如下:
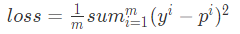
其中 p 表示预测值,y 表示真实值,m 为样本总个数,i 表示第 i 个样本。
最后,我们再使用正规方程解来求得我们所需要的参数。
(3)代码实现流程
1、数据读取
from sklearn import datasets boston = datasets.load_boston() X = boston['data'] Y = boston['target']
2、数据预处理
from sklearn import preprocessing min_max_scaler = preprocessing.MinMaxScaler() X = min_max_scaler.fit_transform(X)
3、将数据集分为训练集和测试集
from sklearn.model_selection import train_test_split test_size = 0.2 seed = 7 X_train,X_test,Y_train,Y_test = train_test_split(X,Y,test_size=test_size,random_state=seed)
4、调用线性模型,得到W
5、房价预测:X_test*W,利用sklearn提供的模型LinearRegression预测房价
LinearRegression的构造函数中有两个常用的参数可以设置:
(1)fit_intercept:是否有截据,如果没有则直线过原点,默认为Ture。
(2)normalize:是否将数据归一化,默认为False。
LinearRegression类中的fit函数用于训练模型,fit函数有两个向量输入:
(1)X:大小为[样本数量,特征数量]的ndarray,存放训练样本
(2)Y:值为整型,大小为[样本数量]的ndarray,存放训练样本的标签值
LinearRegression类中的predict函数用于预测,返回预测值,predict函数有一个向量输入:
X:大小为[样本数量,特征数量]的ndarray,存放预测样本
LinearRegression的使用代码如下:
from sklearn.linear_model import LinearRegression LinearRegression() lr = LinearRegression() #训练模型 lr.fit(X_train,Y_train) #获取预测标签 y_pred = lr.predict(X_test)
(4)具体代码实现
#============1、线性回归方法用于波士顿房价预测========= import numpy as np import pandas as pd import matplotlib.pyplot as plt from sklearn import datasets from sklearn.model_selection import train_test_split from sklearn import preprocessing #***********该函数用于求解正规方程解**************** def mylinearmodel(X,Y): ones=np.ones((X.shape[0],1)) X=np.hstack((ones,X)) XT=X.T XTX=np.dot(XT,X) XTX_1=np.linalg.inv(XTX) XTX_1XT=np.dot(XTX_1,XT) W=np.dot(XTX_1XT,Y) return W #**************均方误差************** def mse(y_predict,y_test): mse = np.mean((y_predict-y_test)**2) return mse #*************决定系数**************** def r2_score(y_predict,y_test): r2 = 1-mse(y_predict,y_test)/np.var(y_test) return r2 #***********预测房价***************** def prediction(X,W): ones=np.ones((X.shape[0],1)) X=np.hstack((ones,X)) y_predict=np.dot(X,W) return y_predict #**********读取数据****************** boston = datasets.load_boston() X = boston['data'] Y = boston['target'] #**********数据预处理-归一化********* min_max_scaler = preprocessing.MinMaxScaler() X=min_max_scaler.fit_transform(X) test_size = 0.2 seed = 7 X_train,X_test,Y_train,Y_test = train_test_split(X,Y,test_size=test_size,random_state=seed) W = mylinearmodel(X_train,Y_train) y_predict = prediction(X_test,W) loss = r2_score(y_predict,Y_test) print(loss) #=======2、利用sklearn中的Lineargression函数预测房价========= import numpy as np from sklearn import datasets from sklearn.model_selection import train_test_split from sklearn.linear_model import LinearRegression from sklearn.metrics import r2_score lr = LinearRegression() lr.fit(X_train,Y_train) y_pred = lr.predict(X_test) loss = r2_score(Y_test,y_pred) print(loss)
(5)scikit-learn线性回归实践 - 波斯顿房价预测(简化版本)
要求:使用sklearn构建线性回归模型,利用训练集数据与训练标签对模型进行训练,然后使用训练好的模型对测试集数据进行预测,并将预测结果保存到./step3/result.csv中。
实现流程:需要调用 sklearn 中的线性回归模型,并通过波斯顿房价数据集中房价的13种属性与目标房价对线性回归模型进行训练。调用训练好的线性回归模型,来对房价进行预测。
#encoding=utf8 mport numpy as np import pandas as pd from sklearn.linear_model import LinearRegression #获取训练数据 train_data = pd.read_csv('./step3/train_data.csv') #获取训练标签 train_label = pd.read_csv('./step3/train_label.csv') train_label = train_label['target'] #获取测试数据 test_data = pd.read_csv('./step3/test_data.csv') lr = LinearRegression() #训练模型 lr.fit(train_data,train_label) #获取预测标签 predict = lr.predict(test_data) #将预测标签写入csv df = pd.DataFrame({'result':predict}) df.to_csv("./step3/result.csv",index=False)


