《机器学习(周志华)》笔记--线性模型（1）--凸函数、损失函数、线性模型的基本形式、线性回归、w* 的代码实现

一、预备知识

1、凸函数

　　凸函数：对于一元函数f(x)，如果对于任意tϵ[0,1]均满足  f(tx₁+(1−t)x₂) ≤ tf(x₁)+(1−t)f(x₂) 。

　　凸函数特征：

　　　　（1）凸函数的割线在函数曲线的上方。

　　　　（2）凸函数具有唯一的极小值，该极小值就是最小值。也就意味着我们求得的模型是全局最优的，不会陷入局部最优值。

                      

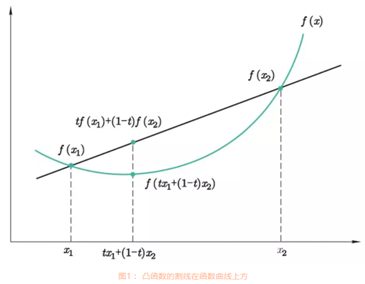
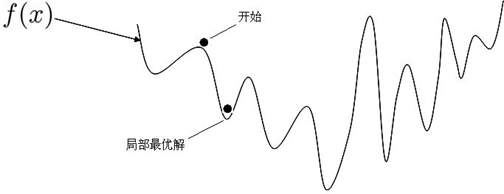
　　　　　　　　　图 1.1.1                                                                                               图 1.1.2

　　判断是否为凸函数方法：

　　（1）对于一元函数  f(x)，我们可以通过其二阶导数  f′′(x)  的符号来判断。如果函数的二阶导数总是非负，即  f′′(x)≥0，则 f(x)是凸函数；例如：f(x)=x²,  f′′(x) = 2。

　　（2）对于多元函数  f(X)，我们可以通过其 Hessian矩阵（由多元函数的二阶导数组成的方阵）的正定性来判断。如果Hessian矩阵是半正定矩阵，则是f(X)凸函数。例如：f(x,y)=x²+y²

　　　Hessian矩阵：

                                        

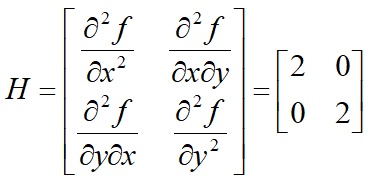
 2、损失函数

　　损失函数用来衡量模型拟合程度的好坏，也就是说当模型拟合误差越大的时候，函数值应该比较大，反之应该比较小。因此，我们的目标就是要使损失函数的值最小，这时学习算法就转化为了一个优化问题。

　　线性回归的损失函数：均方误差函数

　　逻辑回归的损失函数：对数损失函数

　　可以证明，这些都是凸函数，找到了损失函数的极值点，就找到了最优解。极值点对应的就是导数为零的点。

 3、导数

 　　求损失函数需要运用到导数知识。下面列出一些机器学习中常用的求导公式：

　　                                                       

 

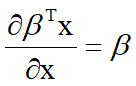
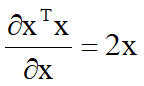
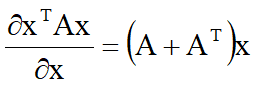
二、线性模型的基本形式

　　给定由 d 个属性描述的示例  x={x₁ ; x₂ ; ... ; x_d } , 线性模型试图学得一个通过属性的线性组合来进行预测的函数：

　　　　　　f(x) = w₁x₁ + w₂x₂ + … + w_dx_d + b

　　一般用向量形式进行表示：

　　　　　　f(x) = w^Tx + b

　　其中 w={ w₁ ; w₂ ; ... ; w_d }，w 和 b 学得之后，模型就得以确定。w 称为权值向量，b 称为偏置，如果只有一个属性，例如，由体重预测身高，f(x) = wx + b，w为斜率，b为截距。

　　线性模型形式简单，易于建模，具有很好的解释性。例如：y=0.2x_色泽+0.5x_根蒂+0.3x_敲声+1

  

三、线性回归

　　线性回归是属于机器学习里面的监督学习，与分类问题不同的是，在回归问题中，其目标是通过对训练样本的学习，得到从样本特征到样本标签直接的映射，其中，在回归问题中，样本的标签是连续值。线性回归是一类重要的回归问题。在线性回归中，目标值与特征直接存在线性关系。

 1、简单线性回归

　　简单线性回归中，一个变量跟另一个变量的变化而变化。

　　那么，到底什么是线性回归呢？如青少年的身高与体重，他们存在一种近似的线性关系：身高/cm = 体重/kg +105 。假如我们将青少年的身高和体重值作为坐标，不同人的身高体重就会在平面上构成不同的坐标点，然后用一条直线，尽可能的去拟合这些点，这就是简单的线性回归。

　　简单的线性回归模型如下：

　　　　y = wx + b

　　其中 x表示特征值(如：体重值)，w表示权重，b表示偏置，y表示标签(如：身高值)。

2、多元线性回归

　　简单线性回归中，一个变量跟另一个变量的变化而变化，但是生活中，还有很多变量，可能由多个变量的变化决定着它的变化，比如房价，影响它的因素可能有：房屋面积、地理位置等等。如果我们要给它们建立出近似的线性关系，这就是多元线性回归。

　　多元线性回归模型如下：

　　　　　　y=b + w1​x1 ​+ w2​x2​ +...+ wn​xn​
　　其中 xi​ 表示第 i个特征值，wi​ 表示第 i个特征对应的权重，b表示偏置，y表示标签。

 3、线性回归一般形式

　　 给定数据集 D = { (x₁,y₁) , (x₂,y₂) , ... ,(x_m,y_m) }, x_i = { x_i1 ; x_i2 ; ... ; x_id }，y_i 是连续的量（实数），线性回归试图学得一个线性模型以尽可能准确预测实值输出标记。即

　　　                               

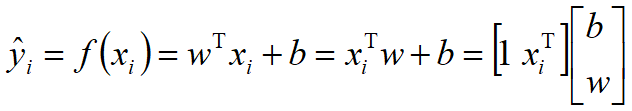
　　其中     ，为增广向量形式。

　　　　                     

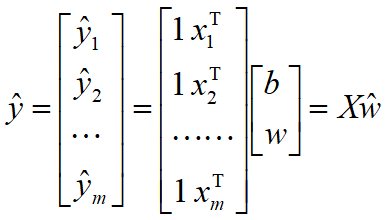
　　其中 ŵ=(b;w) ，数据集 D 表示为一个 m*(d+1) 增广矩阵 X。

　　损失函数：均方误差，用于衡量真实值与预测值之间的差异，公式如下：

                 

                   

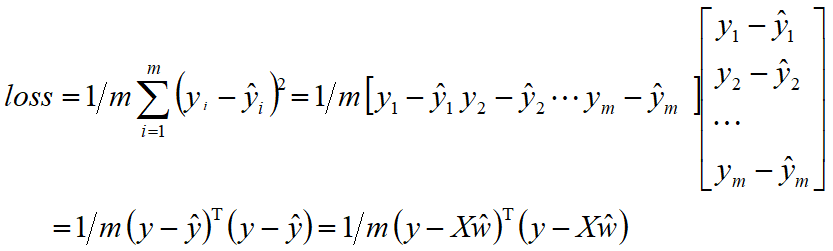
  　　令      对θ求导得到：

　　　　         

　　当X^TX满秩：   

　　其中，X为样本数据构成的m × (d+1) 的矩阵，y是m维标签列向量，上式即维线性回归的正规方程解。然而，现实任务中 X^TX 是不满秩的，这时就会有多个 w*。

　　说明：给定一个包含m个样本的数据集D，xi为第i个样本，每个样本包含d个属性，是一个d维的列向量，yi为第i个样本的标签，在回归任务中，yi是连续的实数。当权值向量w以及偏置确定后，模型就可以确定，这时我们将样本数据xi代入到模型中，就可以可到一个预测值y_hat，可以写成向量形式，其中是增广向量形式，在向量的最左端增加了一个常量1，变成了一个d+1维的行向量，这里1可以看成偏置b的系数，m个样本代入到模型中，可以得到m个预测值，将这些预测值用向量的形式表示为，每一行代表一个样本。w【0】对应的是偏置。

　　回归的目标是使得预测值与真实值之间的差异尽量小，这里使用均方误差来衡量二者之间的差异，记作loss，称为损失函数或代价函数。y所有样本的真实值构成的列向量，y_hat为所有样本的预测值构成列向量。我们的目标转化为求loss最小时权值向量w，导数等于0的点对应极值点。

4、loss最小时权值向量w——w* 的代码实现

　　        当X^TX满秩时，  

　　1、将样本数据转换为增广矩阵形式：

　　　　　　import nump as np

　　　　　　ones=np.ones((X.shape[0],1))

　　　　　　np.hstack((ones,X))

　　2、矩阵转置:

　　　　　　XT=X.T

　　3、矩阵相乘：

　　　　　　XTX=np.dot(XT,X)

　　4、矩阵的逆：

　　　　　　np.linalg.inv(XTX)