《机器学习(周志华)》笔记--模型的评估与选择(6)--衡量分类任务的性能指标:ROC曲线与AUC计算与绘制
五、衡量分类任务的性能指标
5、ROC曲线与AUC
(1)ROC曲线
ROC曲线( Receiver Operating Cha\fracteristic Curve )描述的 TPR ( True Positive Rate )与 FPR ( False Positive Rate )之间关系的曲线。
TPR 与 FPR 的计算公式如下:
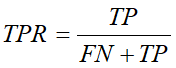

举例:
| 真实\预测 | 0 | 1 |
| 0 | 9978 | 12 |
| 1 | 2 | 8 |
FPR=12/9990=0.0012
TPR=8/10=0.8
分析:
TPR描述的是模型预测Positive并且预测正确的数量占真实类别为Positive样本的比例。
FPR描述的模型预测Positive并且预测错了的数量占真实类别为Negtive样本的比例。
(2)TPR 与 FPR 关系
假设有这么一组数据,菱形代表 Positive,圆形代表 Negtive。

现在需要训练一个逻辑回归的模型对数据进行分类,假如将从 0 到 1 中的一些值作为模型的分类阈值。若模型认为当前数据是 Positive 的概率小于分类阈值则分类为 Negtive ,否则就分类为 Positive (*假设分类阈值为 0.8,模型认为这条数据是 Positive 的概率为 0.7, 0.7 小于 0.8,那么模型就认为这条数据是 Negtive *)。在不同的分类阈值下,模型所对应的 TPR 与 FPR 如下图所示(竖线代表分类阈值,模型会将竖线左边的数据分类成 Negtive,竖线右边的分类成 Positive ):
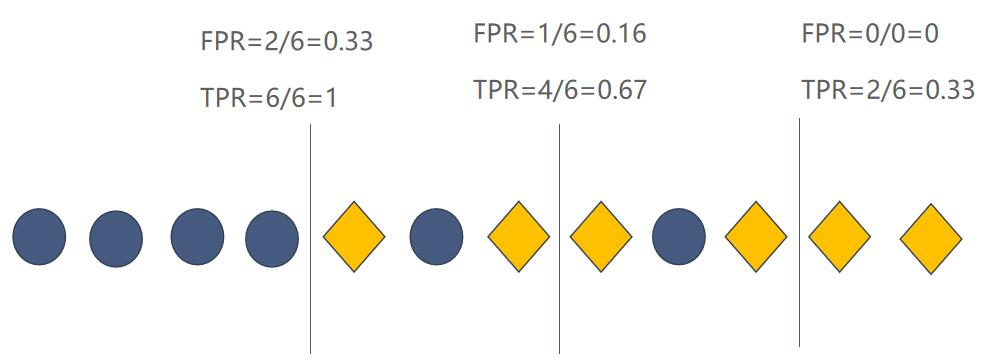
从图中可以看出,当模型的 TPR 越高 FPR 也会越高, TPR 越低 FPR 也会越低。这与精准率和召回率之间的关系刚好相反。并且,模型的分类阈值一但改变,就有一组对应的 TPR 与 FPR 。
举例:
| TPR | 0.20 | 0.35 | 0.37 | 0.51 | 0.53 | 0.56 | 0.71 | 0.82 | 0.92 | 0.93 |
| FPR | 0.08 | 0.10 | 0.111 | 0.12 | 0.13 | 0.14 | 0.21 | 0.26 | 0.41 | 0.42 |
若将 FPR 作为横轴, TPR 作为纵轴,将上面的表格以折线图的形式画出来就是 ROC曲线 :

假设现在有模型 A 和模型 B ,它们的 ROC 曲线如下图所示(其中模型A的ROC曲线为黄色,模型B的 ROC 曲线为蓝色):
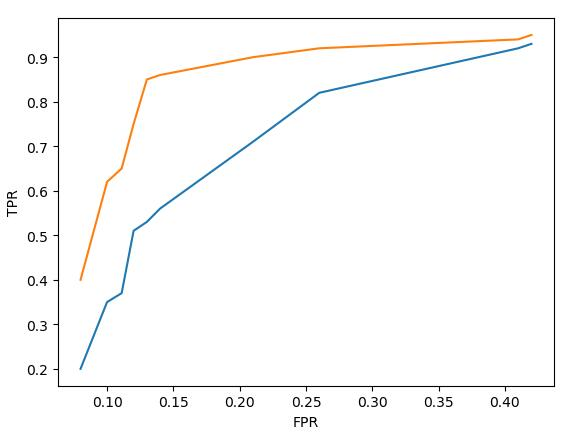
那么模型 A 的性能比模型 B 的性能好,因为模型 A 当 FPR 较低时所对应的 TPR 比模型 B 的低 FPR 所对应的 TPR 更高。由由于随着 FPR 的增大, TPR 也会增大。所以 ROC 曲线与横轴所围成的面积越大,模型的分类性能就越高。而 ROC曲线的面积称为AUC。
(3)AUC
很明显模型的 AUC 越高,模型的二分类性能就越强。AUC 的计算公式如下:
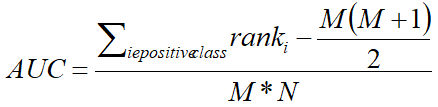
其中 M 为真实类别为 Positive 的样本数量,N 为真实类别为 Negtive 的样本数量。ranki 代表了真实类别为 Positive 的样本点额预测概率从小到大排序后,该预测概率排在第几。
举例:
现有预测概率与真实类别的表格如下所示(其中 0 表示 Negtive, 1 表示 Positive ):
| 编号 | 预测概率 | 真实类别 |
|---|---|---|
| 1 | 0.1 | 0 |
| 2 | 0.4 | 0 |
| 3 | 0.3 | 1 |
| 4 | 0.8 | 1 |
想要得到公式中的 rank,就需要将预测概率从小到大排序,排序后如下:
| 编号 | 预测概率 | 真实类别 |
|---|---|---|
| 1 | 0.1 | 0 |
| 3 | 0.3 | 1 |
| 2 | 0.4 | 0 |
| 4 | 0.8 | 1 |
排序后的表格中,真实类别为 Positive 只有编号为 3 和编号为 4 的数据,并且编号为 3 的数据排在第 2 ,编号为 4 的数据排在第 4。所以 rank=[2, 4] 。又因表格中真是类别为 Positive 的数据有 2 条, Negtive 的数据有 2 条。因此 M 为2, N 为2。所以根据 AUC 的计算公式可知:
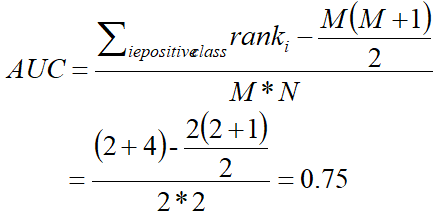
绘制AUC曲线,代码实现:
import numpy as np
def calAUC(prob, labels):
'''
计算AUC并返回
:param prob: 模型预测样本为Positive的概率列表,类型为ndarray
:param labels: 样本的真实类别列表,其中1表示Positive,0表示Negtive,类型为ndarray
:return: AUC,类型为float
'''
f = list(zip(prob,labels))
#zip函数能将列表序列。依次取出组成一个由元组组成的列表
rank = [values2 for values1,values2 in sorted(f,key = lambda x:x[0])]
# 按概率从小到大排序
rankList = [i+1 for i in range(len(rank)) if rank[i] == 1]
# 得到rank
posNum = 0
negNum = 0
for i in range(len(labels)):
if(labels[i] == 1):
posNum += 1
else:
negNum += 1
# 根据公式计算AUC
auc = (sum(rankList) - (posNum*(posNum+1))/2)/(posNum*negNum)
return auc


