《机器学习(周志华)》笔记--绪论（1）--机器学习基本术语、假设空间、归纳偏好

一、引言

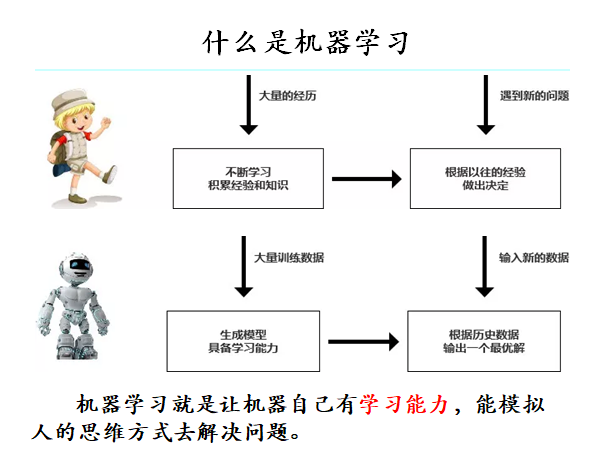
　　机器学习致力于研究如何通过计算的手段，利用经验来改善系统自身的性能。

　　在计算机系统中，“经验”通常以“数据”的形式存在，因此，机器学习所研究的主要内容，是关于在计算机上从数据中产生的“模型”的算法，即“学习算法”。有了学习算法，我们就把经验数据提供给它，它就能基于这些数据产生模型，在面对新的情况时，模型会给我们提供相应的判

                

二、基本术语             　

　　1、属性：反映事件或对象在某方面的表现或性质的事项

　　2、属性值：属性的取值

　　3、属性空间：属性张成的空间

　　4、特征向量：空间中每个点的坐标向量

　　5、标记：关于示例结果的信息

　　6、样例：拥有了标记信息的示例

　　7、数据集：所有样例组成的集合

　　8、学习：从数据中学得模型的过程

　　9、训练集：训练样本组成的集合

　　10、真相(ground-truth):数据的潜在的某种规律

　　11、测试：学得模型后，使用其进行预测得过程

　　12、测试集：测试样本组成得集合

　　13、泛化能力：学得模型应用新样本的能力。

举例：

　　我们已经知道了，机器学习是利用数据，从数据中归纳出规律，并用来对新事物进行预测。所以，机器学习首先要有数据，假设我们收集了一份关于西瓜的数据：

　　               

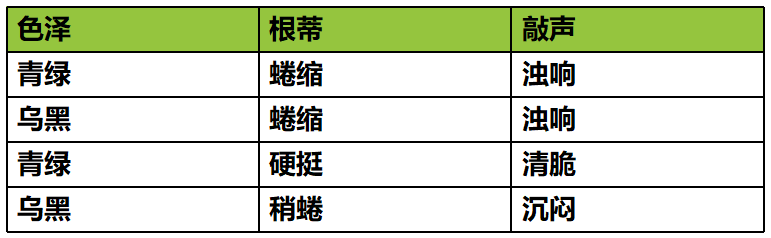
• 我们看到的诸如西瓜数据集这样的一个二维表格就是数据集；

• 我们把数据中的每一行称为一个示例或样本；

• 反映事件或对象在某方面的表现或性质的事项，如：色泽、根蒂、敲声，称为属性或特征；

• 属性上的取值，例如：青绿、乌黑。称为属性值或特征值；

• 属性值形成的集合称为属性空间；

• 我们把一个示例（样本）称为一个特征向量。　　

　　一般地，令 D={x1 , x2 , .. , xm ​} 表示包含 m 个示例的数据集，每个示例由 d 个属性描述（例如上面的西瓜数据使用了三个属性），则每个示例：

　　　　　　　　　　xi = ( xi1; xi2   ...; xid )

　　　　是 d 维样本空间X中的一个向量，xi​∈X，其中 xi​j 是xi在第 j 个属性上的取值。d 称为样本xi​ 的维数。

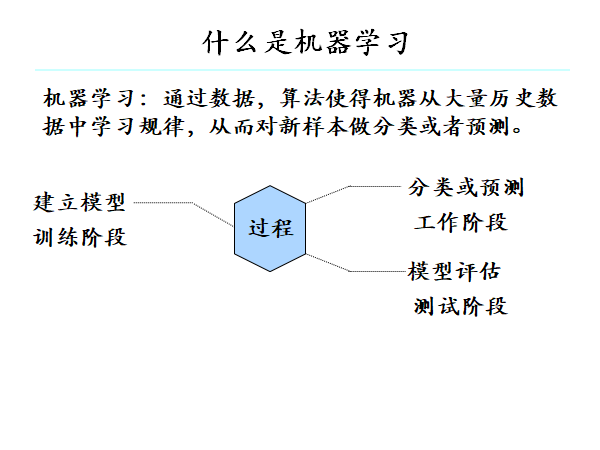
　　有了数据后，机器就可以从数据中进行学习。从数据中学得模型的过程称为“学习”或“训练”，这个过程通过执行某个学习算法来完成。

　　训练过程中使用的数据称为“训练数据”，其中每个样本称为一个“训练样本”，训练样本组成的集合称为“训练集”，学习过程就是为了找出或逼近真相。

　　数据分为训练集和测试集，在测试集上的表现称为泛化能力。在评估泛化能力，通常比较预测值与真实值。

　　根据数据是否有标签，可以将机器学习方法分为有监督方法和无监督方法。

　　如果数据有标签，则为有监督方法。有监督方法的两大类任务，一个是回归，一个是分类。如果标签为连续值，它就是一个回归任务。如果标签数据是离散值，那就是一个分类任务。

　　如果数据没有标签，就属于无监督方法，聚类是一种典型无监督学习方法。俗话说“物以类聚、人以群分”，聚类算法就是将数据划分成不同的组，组内的样本具有很强的相似性，组间的样本具有很强的差异性。

 三、假设空间

　　14、归纳：特殊到一般的泛化过程

　　15、演绎：从一般的特殊的特化过程

　　16、概念学习：要求从训练数据学得概念。

　　17、布尔概念学习：对是、不是这样的可以表示成0/1布尔值的目标概念学习。

　　假设空间在已知属性和属性可能取值的情况下，对所有可能满足目标的情况的一种毫无遗漏的假设集合。

　　归纳和演绎是推理的两大手段，归纳是特殊到一般的泛化过程，即从具体的事实归结出一般性的规律，演绎是从一般到特殊的特化过程。

　　从样例中学习的过程很显然是一个归纳的过程，因此也成为归纳学习。归纳学习有狭义和广义之分，广义的归纳学习大致相当于从样例中学习，而狭义的归纳学习则要求从训练数据中学的概念(concept)，因此亦称为“概念学习”或“概念形成”。

　　概念学习最基本的形式是布尔概念学习，即对“是”“不是”这样的可表示为0/1布尔值的目标概念的学习。

举例：

　　       

　　学习得“好瓜”这样一个概念可以用一个布尔表达式进行表示：

　　　　　　      

　　问号表示尚未确定的取值，我们学习目标为“好瓜”，通过学习，将这些问号确定下来，确定问号的取值就是学习的过程。

　　学习的过程可以看作一个在所有假设组成的空间中进行搜索的过程。搜索目标是找到与训练集“匹配”的假设，即能够将训练集中的瓜判断正确的假设。除此还有一种取值用通配符*表示，表示无论取什么值都合适。空集符号表示一种极端的概念，也许世界上根本不存在好瓜。假设的表示一旦确定，假设空间及其规模大小就确定了。

　　举个例子，假设西瓜的好坏由“色泽”，“根蒂”以及“敲声”决定，且"色泽"、"根蒂"和"敲声"分别有3、3、3 种可能取值。

　　　　假设空间的大小即为：(3+1)*(3+1)*(3+1)+1=65

　　     　　

　　可以有许多策略对这个假设空间进行搜索，例如自顶向下、从一般到特殊，或是自底向上、从特殊到一般，搜索过程中可以不断删除与正例不一样的假设、和（或）与反例一致的假设。最终将会获得与训练集一致（即对所有训练样本能够进行正确判断）的假设，这就是我们学得的结果。

　　现实问题中我们常面临很大的假设空间，但学习过程是基于有限样本训练集进行的，因此，可能有多个假设和训练集一致，即存在着一个与训练集一致的“假设集合”，我们称之为“版本空间”(version space)。

　　版本空间构建过程：对假设空间进行搜索，可以自顶向下（一般到特殊），也可以自底向上（特殊到一般），在搜索过程中只保留与训练集正例一致的假设。

分析：

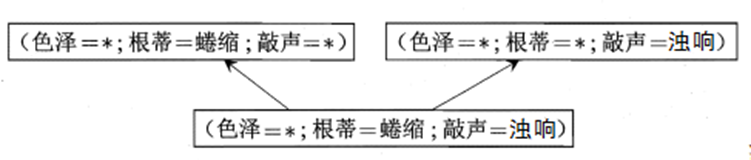
　　新瓜：（色泽=青绿，根蒂=蜷缩，敲声=沉闷），

　　　　（1）对于假设  (色泽=*) ⋀ (根蒂=蜷缩) ⋀ (敲声=*)，判断好瓜

　　　　（2）对于假设（色泽=*) ⋀ (根蒂=蜷缩) ⋀ (敲声=浊响)，判断坏瓜。

                  

四、归纳偏好

　　归纳偏好(简称"偏好")：机器学习算法在学习过程中对某种类型假设的偏好。说白了就是“什么样的模型更好”这一问题。

　　归纳偏好可看作学习算法自身在一个可能很庞大的假设空间中对假设进行选择的启发式或“价值观”。而在具体的现实问题中，学习算法本身所做的假设是否成立，也即算法的归纳偏好是否与问题本身匹配，大多数时候直接决定了算法能否取得好的性能。

　　“奥卡姆剃刀”(Occam's razor)：是一种常用的、自然科学研究中最基本的原则，即“若有多个假设与观察一致，则选最简单的那个”。

　　没有免费的午餐定理（NFL）：无论一个算法多么笨拙，无论一个算法多么聪明，他们的期望性能相同。脱离具体问题，空泛谈论“什么学习算法更好”毫无意义。