python之递归

递归就是不断的调用自己示例：

import sys

# print(sys.getrecursionlimit())  # 默认最大递归限制：1000
# sys.setrecursionlimit(999999999)  # 不管数值多大，最多到20963册


def recursion(n):
    print(n)
    recursion(n + 1)


recursion(1)递归与栈的关系

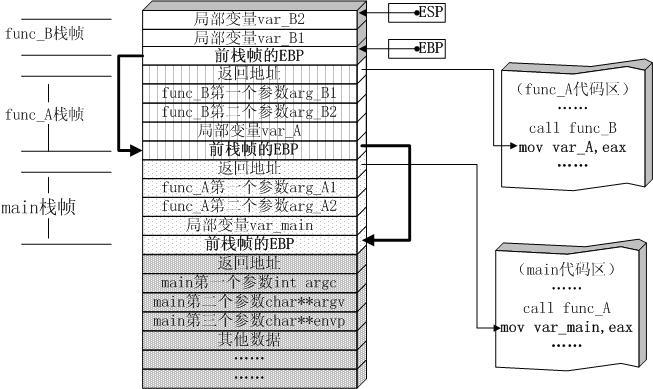
在计算机中，函数调用时通过栈(stack)这种数据结构实现的，每当进入一个函数调用，栈就会加一层栈帧，每当函数返回，栈就会减一层栈帧。

由于栈的大小不是无限的，所以，递归调用的次数过多，就会导致栈溢出。

 

递归的特点：

1. 必须有一个明确的结束条件，要不就会变成死循环了，最终撑爆系统
2. 每次进入更深一层递归时，问题规模相比上次递归都应有所减少
3. 递归执行效率不高，递归层次过多会导致栈溢出

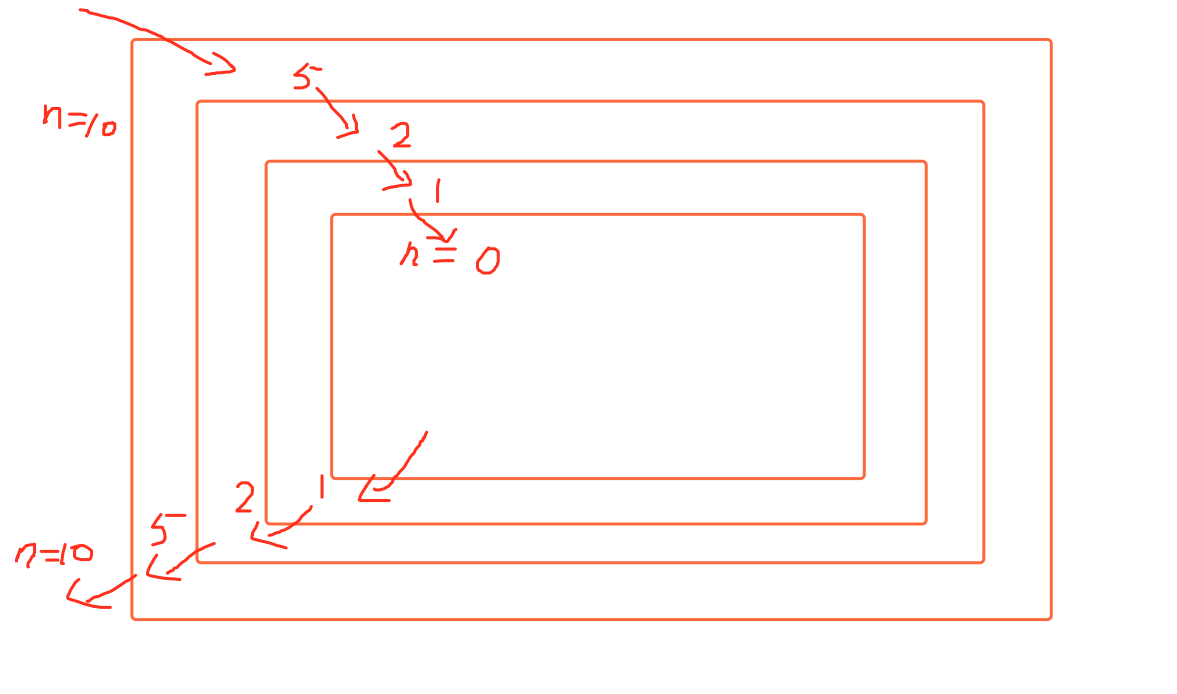
def zero(n):
    n = n // 2
    print(n)
    if n == 0:
        return 'Done'
    zero(n)
    print(n)  # 1 2 5


'''
第一层会n=5，第二层会n=2，第三层会n=1，第四层n=0,符合条件程序停止。停止之后，程序的控制权会回到第三层调用第四层的位置，也就是zero(n)，然后print出1，然后回到第二层print出2,最后回到第一层print出5。
整个程序是先一层层进去，然后在一层层出来。
'''
zero(10)  # 5 2 1 0 1 2 5

图示：

 

 

阶乘
n! = n * (n-1)

def factorial(num):
    if num == 1:
        return 1
    return num * factorial(num - 1)


print(factorial(10))

 

二分查找

data_set = list(range(101))


def b_search(num, low, high, data):
    mid = int((low + high) / 2)
    if low == high:
        print('cannot find it ')
        return
    if data[mid] > num:
        b_search(num, low, mid - 1, data)
    elif data[mid] < num:
        b_search(num, mid + 1, high, data)
    else:
        print('find it', data[mid])


b_search(33, 0, len(data_set), data_set)

尾递归优化
执行完一层调用下一层的时候，把这一层的数据给销毁掉,并且下一层和这一层没有关系，叫尾递归。
阶乘不是尾递归  return num * factorial(num - 1) 因为num还在等着factorial(num - 1)的结果。

def cal(n):
    print(n)
    return cal(n + 1)  # 虽然这用的是尾递归优化，但是python不支持尾递归优化，C语言和JS支持。


cal(1)