算法图解之广度优先算法

一、用途

广度优先算法是为了解决两样东西之间的最短距离，其中最短距离的含义很多，如：

• 编写国际跳棋AI，计算最少走多少步就可获胜
• 编写拼写检查器， 计算最少编辑多少个地方就可将错拼的单词改成正确的单词
• 根据你的人际关系网络找到关系最近的医生

二、图

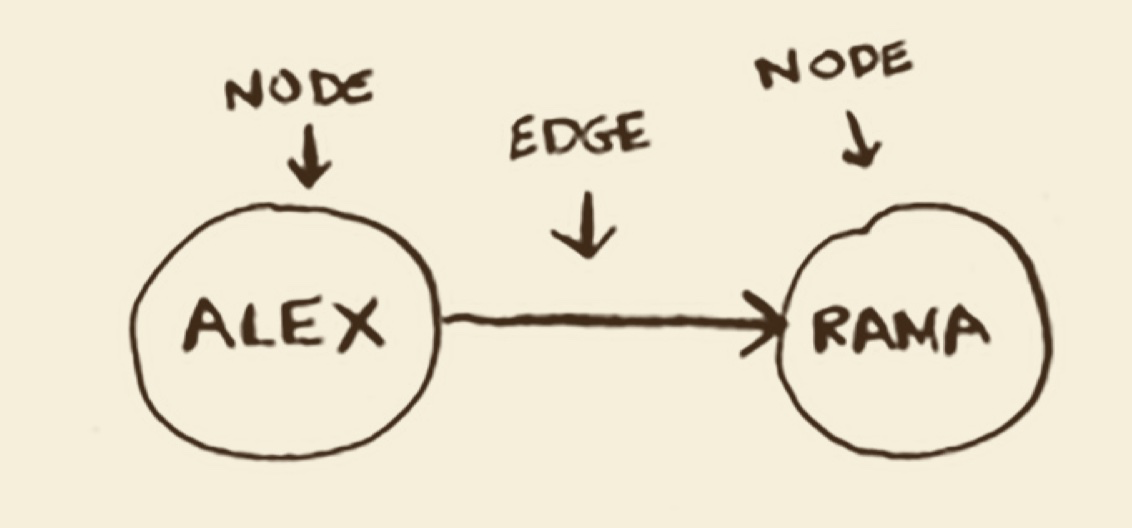
图由节点和边组成，模拟一组链接。

 

 三、广度优先搜索

应用场景

• 从节点A出发，有前往节点B的路径吗？
• 从节点A出发，前往节点B的哪条路径最短？

问题：你经营着一个芒果农场，你要找一个芒果销售商并把芒果卖给他。

解决思路：你需要优先从你的朋友中开始找，朋友中没有，再从朋友的朋友中找，在找完所有朋友之前，不去找朋友的朋友。以此类推。如下图所示：

 

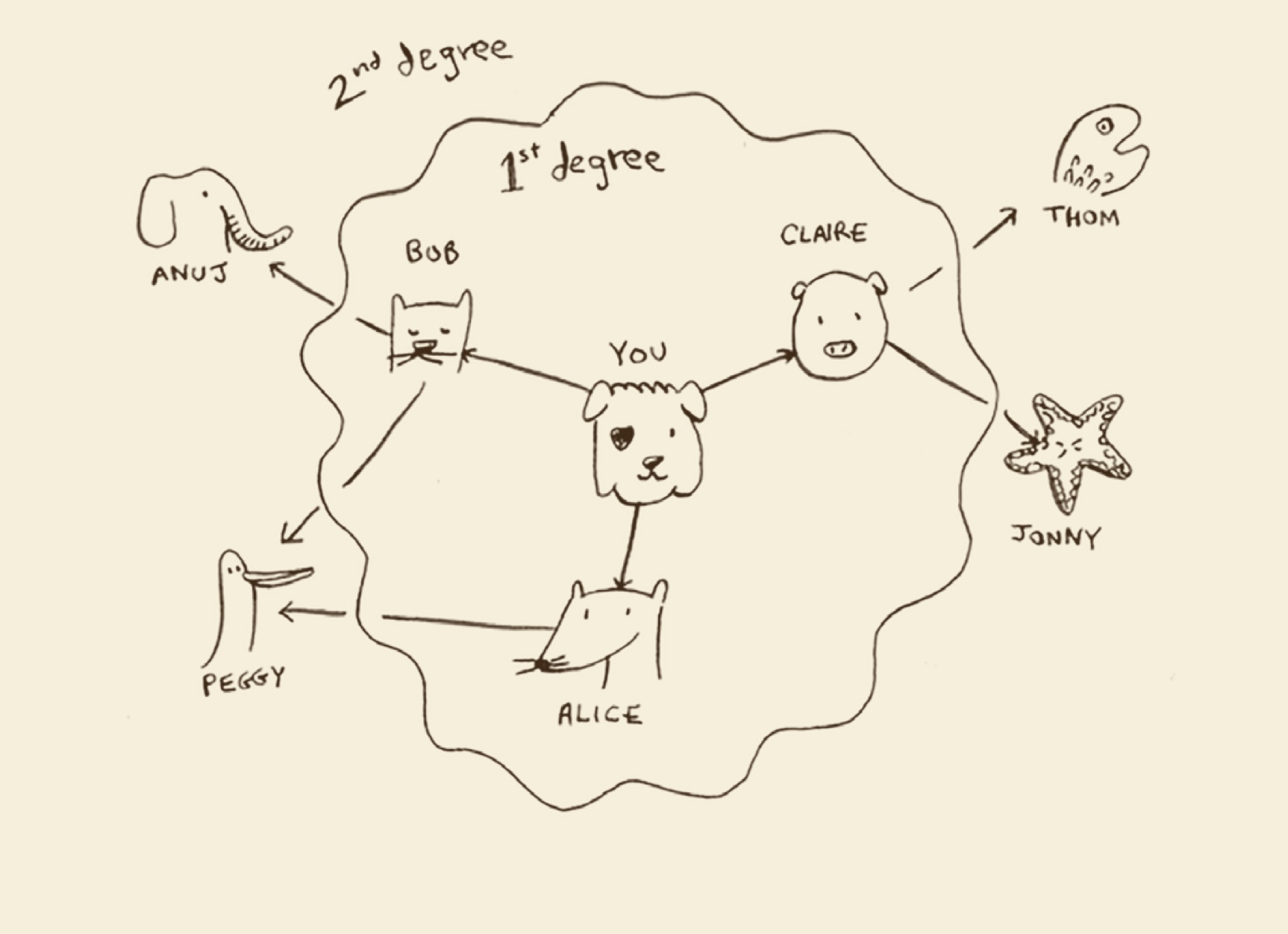
这就需要按顺序进行添加，并按顺序进行查找，有一种数据结构可以实现这个目的，就是队列。

 

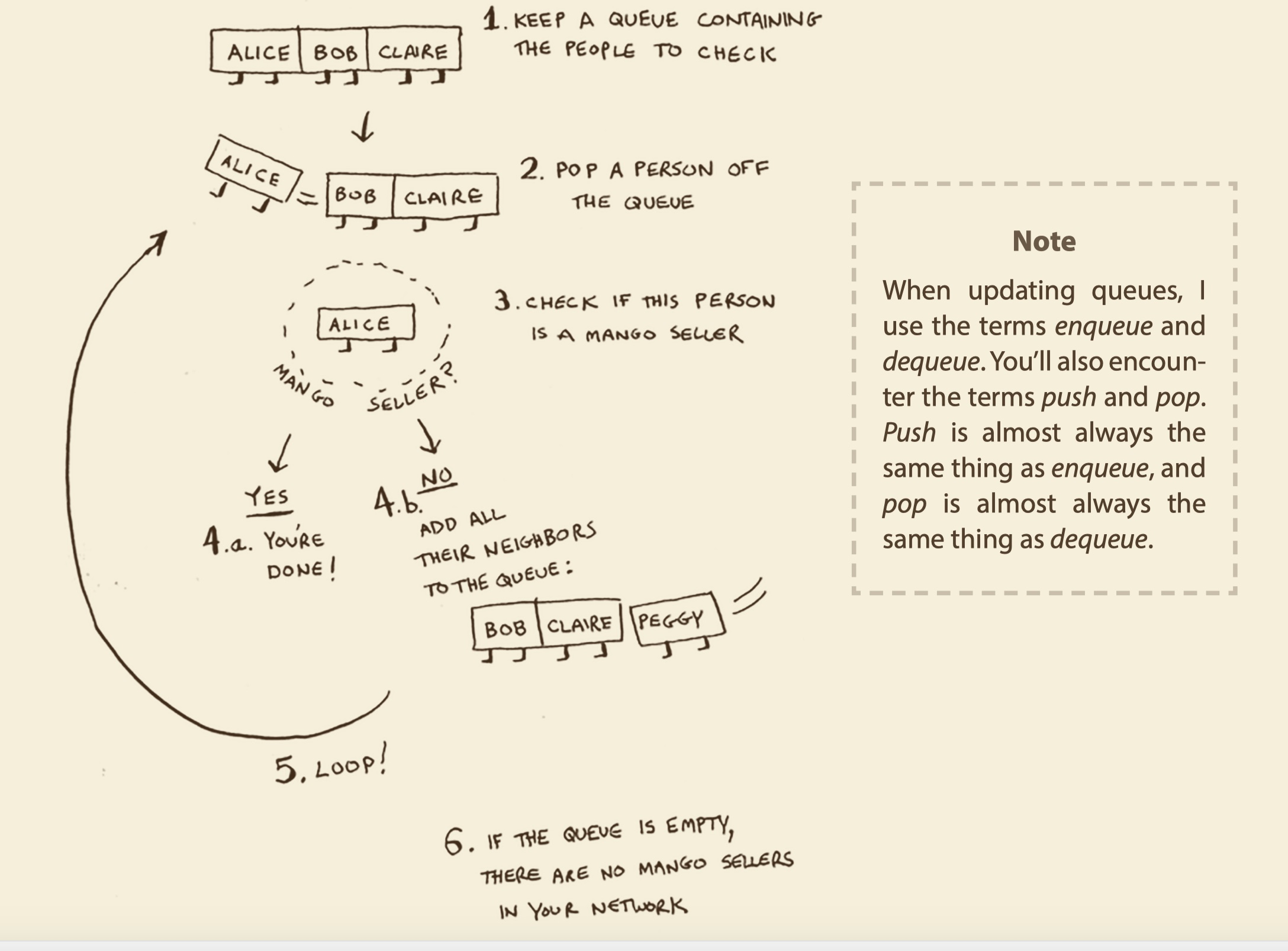
四、队列（Queues）

队列的工作原理就和在医院排队挂号一张，排在前面的先挂号。

队列是一种先进先出（First In First Out）的数据结构，而栈是一种后进先出（Last In First Out，LIFO）的数据结构。

队列图示：

 

 

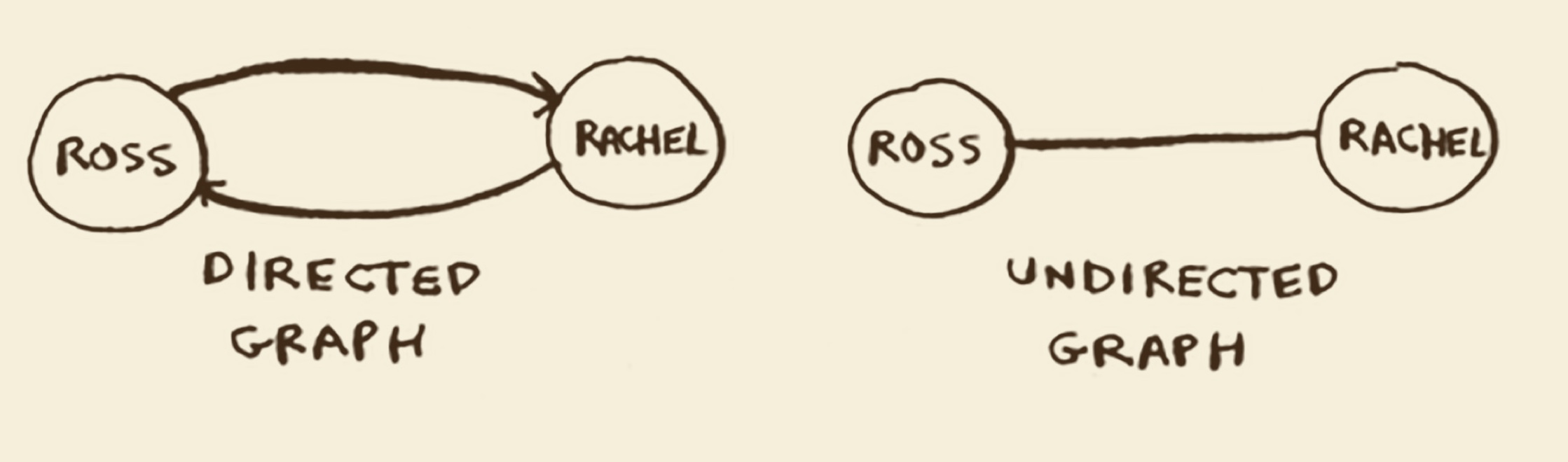
五、有向图和无向图

 

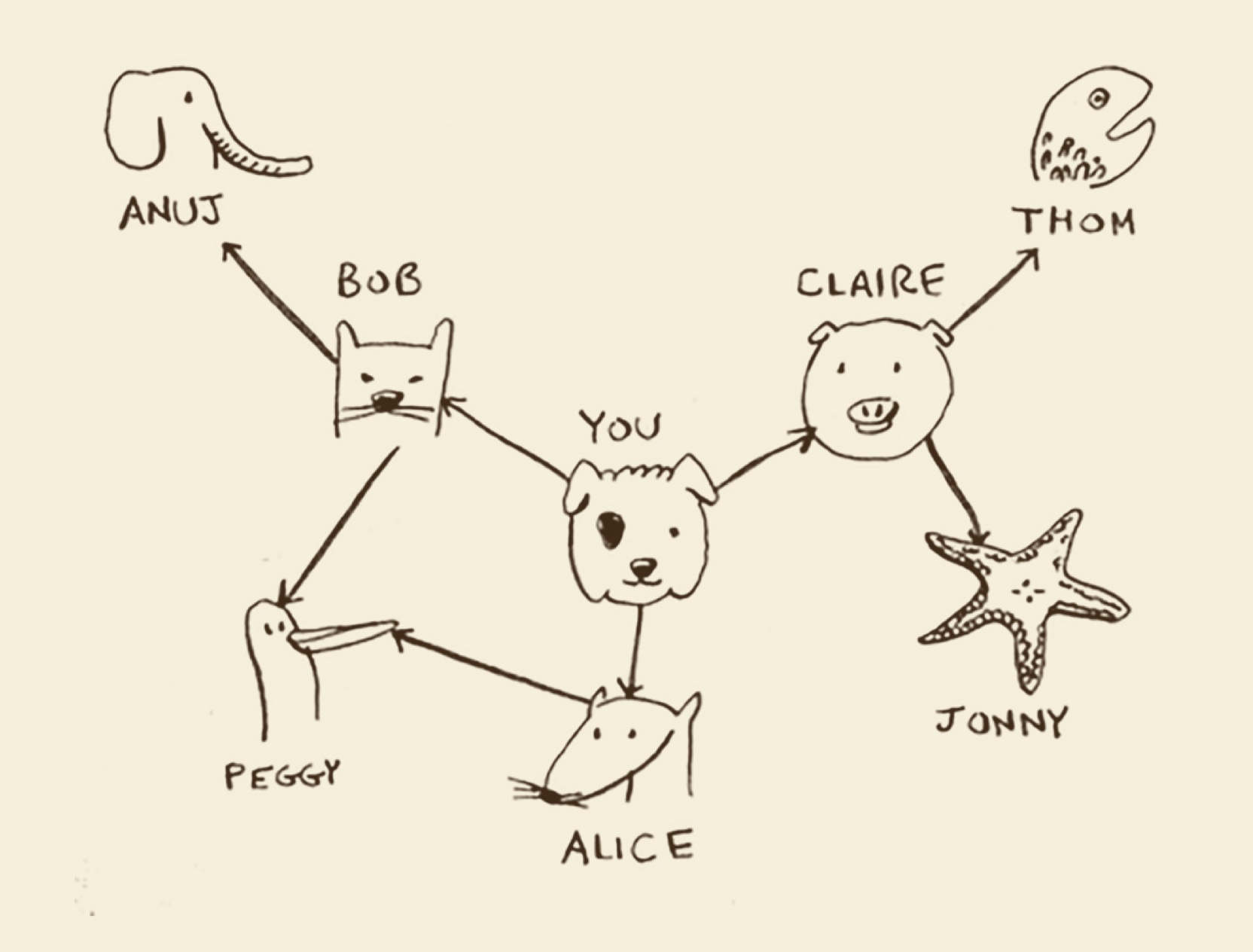
有箭头指向自己，但是没有从自己指向其他人的箭头，这被称为有向图（directed graph），其中的关系是单向的。 （Anuj、Peggy、Thom、Jonny）

直接相连的节点互为邻居，被称为无向图。

 

六、实现算法

from collections import deque

graph = {}
graph['you'] = ['alices', 'bobs', 'claires']
graph['bobs'] = ['anujs', 'peggys']
graph['alices'] = ['peggys']
graph['claires'] = ['thoms', 'jonnys', 'jack']
graph['anujs'] = []
graph['peggys'] = []
graph['thoms'] = []
graph['jonnys'] = []
graph['jack'] = ['lucy', 'mango_andrew']
graph['lucy'] = []
graph['mango_andrew'] = []


def person_is_seller(name):
    return 'mango' in name


def search(name):
    search_queue = deque()
    search_queue += graph[name]
    searched = []

    while search_queue:
        person = search_queue.popleft()

        if person not in searched:
            if person_is_seller(person):
                print(person[6:] + ' is a mongo seller')
                return True
            else:
                search_queue += graph[person]
                searched.append(person)
    print('Not find mango seller')
    return False


search('you')

 

顺便提一下，字典这么写是为了看起来更清晰，它的添加顺序对结果是没有影响的，因为散列表是无序的。

graph['you'] = ['alices', 'bobs', 'claires']
graph['bobs'] = ['anujs', 'peggys']

# 写成下面这样对结果一点影响都没有
graph['bobs'] = ['anujs', 'peggys']
graph['you'] = ['alices', 'bobs', 'claires']

 

 

 

 

七、运行时间

你在整个人际关系网中搜索芒果销售商，就意味着你需要沿每条边前行（一个人到另一个人的箭头），时间至少为O(边数）。将每一个人添加到队列的时间是O(1)，因此广度搜索的运行时间为O（人数 + 边数），通常写作O(V+E)，其中V为定点（vertice），E为边数。