算法图解之分而治之

谓“分而治之” 就是把一个复杂的算法问题按一定的“分解”方法分为等价的规模较小的若干部分，然后逐个解决，分别找出各部分的解，把各部分的解组成整个问题的解。注意分而治之不是算法，而是一种解决问题的思路

工作原理

1) 找出简单的基线条件；

(2) 确定如何缩小问题的规模，使其符合基线条件。

 

例子

 假设你要将一块地（1680m * 640）均匀地分成方块，且分出的方块要尽可能大。

首先找出基线条件：最容易处理的情况是，一条边的长度是另一条边的整数倍。如果一边长25 m，另一边长50 m，那么可使用的最大方块为 25 m×25 m。换言之，可以将 这块地分成两个这样的方块。

然后找出递归条件：，这正是D&C的用武之地。根据D&C的定义，每次递归调用都必须 缩小问题的规模。

具体操纵

把这块土地划出两个640m * 640m 

 

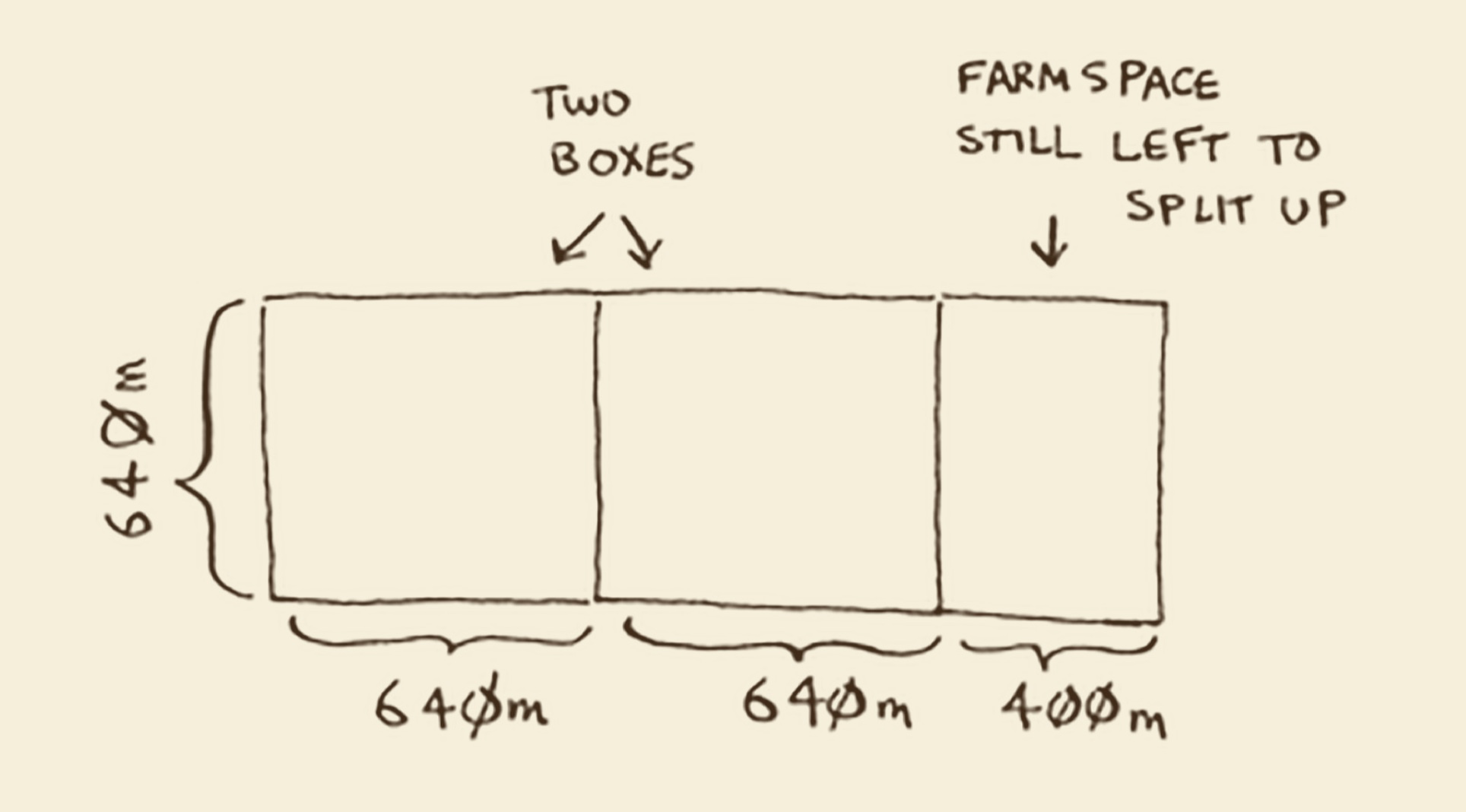
然后我们的问题就成了640 * 400 ,我们只需要去关心这小块土地的划分就好了。当我们从这小块土地划分出了它的最大方块，我们就剩下了这小块土地的一块小土地，我们这时候只去关心新划分的这一块土地就好。这其实用到了递归的思想，需要注意的是适用于这小块地的最大方块，也是适用于整块地的最大方块。这用到了欧几里得算法，这里有证明：欧几里得算法。 最后我们划分出80 * 80m。