超计算（Hyper computation）模型

作者：Xyan Xcllet
链接：https://www.zhihu.com/question/21579465/answer/106995708
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

超计算，是一个研究比图灵机计算能力更强的计算能力的计算机器的理论计算机科学分支。

主要有以下部分模型：

A.谕示机.带“黑箱”的图灵机。由图灵本人亲自提出，“黑箱”就是一个谕示，经过一个谕示就可以得到一个问题的判定结果。所有Hypercomputation的“原型机”。后来的大部分计算模型都是基于谕示机的概念，将其他特性引入图灵机中使其不受先前的计算能力限制而得到新的模型。

B.Blum–Shub–Smale machine. 可以在实数域内计算并可以储存无限精度的实数（而经典图灵机只能储存可计算数。）而它对应的计算时间是离散的。但是，如果图灵-丘奇论题在我们宇宙中为真，那么宇宙中就不存在实数，只存在可计算数。

P.S. Blum–Shub–Smale machine 的配置是一个四元组： $(k,r,w,x)$ ，其中 k 是当前执行指令的数量, r 和 w 是复制寄存器（copy registers）， x 是存储在 BSS machine 所有寄存器内的内容。机器的计算由配置 $(0,0,0,x)$ 开始，在 k = N （N 为 indexed）时结束计算。而 x 的最终内容被认为是该机器的输出。

C.量子计算机. 曾经有量子计算机可以使用一个无限叠加状态的量子力学系统来计算不可计算函数的提议，不过在现实的量子计算机中不可能做到。量子计算机的计算能力在本质上与图灵机等价，但在计算复杂度上可以优于图灵机（如果这也算是计算能力的话。）。现实中的量子计算机的计算能力可以在多项式时间内解决 BQP ，并没有想象中的那么强。

但是，尽管目前可以通过结构与算法优化使计算能力不断提高，但量子计算机的计算能力还是有真正的上限的：即布莱梅曼极限（Bremermann's limit）。在量子物理框架下，我们宇宙中所有物质的计算能力都不可能超过每千克 $\frac{c^{2} }{\hbar }$ bits/s（h为普朗克常数，c为光速）这也是量子计算机真正无法逾越的计算速度极限。而且你也不可能真正地达到该极限，因为所需能量会使你的计算机直接坍塌成一个黑洞。

最后值得一提的是，只要对量子力学中算符的线性要求做些微的放宽，例如，温伯格引入的非线性算符（这些工作出现在温伯格试图研讨的所谓非线性量子力学中）得到允许，则我们可以在新型量子计算机上用多项式时间求解 PSPACE 完全问题（ NP 完全问题自然不在话下）。

D.相对论时间效应

在相对论中，不同物体参考系的时间流逝不一样，如果我们能让计算机参考系在时间流逝上快很多，那我们也变相得解决了这个问题。

一台计算机留在地球上让它做一个复杂的计算问题，然后操作者登上一个航天器，加速到接近光速，一段时间后减速再返回地球。根据：

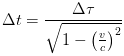
$\Delta t$ 为地球计算机的时间， $\Delta \tau$ 为操作者的时间，c 为光速。如果操作者可以找到电脑并且它还在运行的话，就可以知道那个复杂问题的答案了。

不过这要使计算机进行指数级的加速，必须让速度指数级接近于光速，这也意味着所需要的能量指数级增长，而因为能量密度不可能大于黑洞，这也意味着计算机的大小必须指数级增长，某种程度上来说就是 EXPSPACE ，这是不可取的(建造指数级数量的计算机同时计算可达到同样效果)。

E. 封闭类时曲线计算机. 依靠广义相对论中拥有闭合时间曲线的封闭类时曲线 (closed timelike curve, CTC) 时空来计算—给计算机配一台时间机器。

在计算理论中，人们比较感兴趣的问题之一是，NP 问题，比如哈密尔顿回路问题（判断一个图是否有圈经过每个顶点恰好一次），是否可以在多项式时间内被解决。然而即使是引入了量子计算后，这个问题也一直悬而未决。

20世纪后期，学者们开始探讨是否存在在计算能力上可以超越量子计算的模型以及它们的物理实现可能性。

物理学家 Deutsch 提出，如果我们在时间本身上做手脚呢？

于是就有了利用封闭类时曲线来进行加速计算的提议。

但是，利用 closed timelike curve 来做时间旅行的话，就不得不面对一个悖论，即祖父悖论。

目前解决祖父悖论的方法有很多，封闭类时曲线计算机采用的是这个（虽然有很多科学家并不认同这种解决方法。）：

你回到过去杀掉祖父的可能性为 50%，于是你祖父生下你的父母可能性也为 50%，这样你回到过去的可能性就是 50%，如此循环。于是你和你的祖父其实都是“存在”和“不存在”的叠加，可能性各是 50% （ $\frac{1}{2}$ ）。

那么为什么是 50% 的可能性呢？试想，如果你有 1/3 （ $\frac{1}{3}$ ）的可能性回去杀掉祖父，那么他生下你父母的可能性就变为 2/3，于是你回到过去杀人的可能性就是 2/3（ $\frac{2}{3}$ ），而不是我们所假设的 1/3。这样就出现了因果不连续。大自然不允许这样的情况存在（出现悖论），所以它强迫你必须以 50% 的可能性存在。也就是说，如果你进行了“回到过去杀掉祖父”这一行动，那么大自然说，你的存在必然是 50% 的可能。在量子机制框架下，CTC是自洽的。简单的解释下，就是这个世界是个概率空间，以马尔可夫过程的方式进行运作，如果每次新的概率分布和原来的一样，马尔可夫过程的稳定分布则是一组解。那么，这样就可以避免祖父悖论了。没有任何矛盾。

（补充内容）也就是说，如果我们让 $|\varphi \rangle$ 为"更年轻"版载体粒子的初始态，让 $\hat{\rho }$ 为与其互动的"更老"版载体粒子的密度算符。然后进入一区域这两个粒子进行相互作用的联合密度算符是：

$|\varphi \rangle \langle\varphi |\otimes \hat{\rho }$

而两粒子在相互作用后的密度算符为： $U\left ( |\varphi \rangle \langle\varphi |\otimes \hat{\rho } \right )U^{\dagger }$

而量子一致性条件要求, 当它离开交互区域时, 更年轻版的粒子的密度算子(符)与它进入交互区域时的更老版相同：

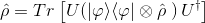
这个 $\frac{1}{2}$ 为 Fixed-point，即不动点。这个不动点确保了自然的运行依然符合因果定律。而且大自然会以某种神奇的机制自动的寻找这个“不动点”，以使整个系统因果连续（历史自治）。

封闭类时曲线计算机具体的计算原理是这个："莎士比亚戏剧"。

一个人抄下莎士比亚全集，然后回到过去将其交给莎士比亚本人。

于是莎士比亚全集就这么凭空产生了。

原因是，为了保证“那个人”能够“阅读到”莎士比亚全集（否则他不可能知道有这么个东西），它必须足够出名。而既然他已经带着它回到过去，那么为了维护因果连续，大自然这个系统为我们“写”了一个足够出名的东西出来。这个东西就是莎士比亚全集，即不动点。

当然，系统同时也曾经尝试过无数其他的“作品”，甚至一些不成话的乱码。

这样一台计算机，能够随时进行指向过去的时间旅行。并且，它能够利用我前面提到的封闭类时曲线（CTC）来解决一些一般情况下非常难以解决的问题。

具体地，比如说“大数分解”问题。

首先，我得给它一个大数，并期望它输出这个数的任一个因数（除了1）。一般来说，普通计算机也许会在运行100万年以后给出答案（如果它一直不死机），而封闭类时曲线计算机却能在短短1秒钟之内（也许更短）给出答案。

它怎样工作呢？首先，在输入数据 A 之后，它记下这个时刻 t ，同时，它得到了一个神秘的输入数据 x。然后它检查“ x 是否是 A 的因数 ”。如果不是，则 x = x+1，同时如果 x > A ，则 x = 2。之后输出 x，并利用封闭类时曲线进行时间旅行回到 t 时刻，将 x 输入自身。

很明显，这是一个循环，只不过这个循环运行在时间上。而大自然为了维护因果连续，会不断的做这个循环，寻找这个让因果连续和历史自治的不动点，即 "x 是 A 的因数" ；直到输入的 x 与输出的 x 相同为止，即直到 x 确实是 A 的因数为止。所以在我们看来，这台电脑会在1秒钟内直接输出我们想要的 x。

这就相当于是这个时间机器的时间循环帮我们计算了所有可能性，在一秒钟内的不断循环计算之内给出了答案。也就是说，如果封闭类时曲线存在，计算机可以“强迫”自然去解决复杂的组合问题，仅为了让宇宙的历史保持一致(比如，去阻止类似祖父悖论这样的东西的出现)。而且在这些复杂的组合问题里面就包括了 PSPACE（包括 PSPACE -complete ， NP 类型，也包括了 NP-complete ），甚至可能包涵图灵不可计算问题。

另外，记 $P_{CTC}$ , 为允许封闭类时曲线的多项式时间可计算的问题。 $BQP_{CTC}$ 是结合量子计算机时多项式时间可计算的问题。它们俩能解决地的计算问题级别是等价的：都可以解决PSPACE。

如果 Deutsch 的封闭类时曲线可以允许计算任意长度的字符串，则封闭类时曲线计算机可以判定停机问题。

P.S. 补充说明，以上的 CTC 计算机的计算原理和计算能力是基于 Deutsch 的模型。除此之外，学术界还存在着其他解决祖父悖论的方法，在此之上提出了另一种 CTC 计算机模型。

2009年，另一位物理学家 Seth Lloyd 给出了利用另一种 CTC 模型进行计算的方法，该模型中封闭类时曲线的存在是基于量子态隐形传输和事后选择（post-selection）算法。与 Deutsch 的封闭类时曲线不同的是，Deutsch 的模型会导致相关性破坏效应，即时间旅行者从 Deutsch 的 CTC 出来进入的宇宙，与他在未来的退出（即他之前所在的那个宇宙）无关。相比之下,后选择 CTC 保持了相关性,这样时间旅行者回到他记忆中的同一个宇宙。

Seth Lloyd 的模型解决祖父悖论的方式如下：

运用 Post-selection 算法能够确保某一特定类型的量子信息态进行隐形传输，而将其他量子信息过滤掉。只有经“后选择”算法认定传输前后能自相一致的量子信息态，才有资格得到这种“通行证”，进行隐形传输，形成一个自治、不产生矛盾的环境状态。而且 Post-selection 会决定只有有限类型的量子态能被远距传输，即在远距传输前原始物体的量子态也被局限了，由于时间旅行的结果属于有限概率，祖父悖论将不可能发生。

但是，Seth Lloyd 的模型会削弱封闭类时曲线的计算能力。在 Deutsch 模型中，无论是配经典图灵机还是量子图灵机，都可以解决全部 PSPACE。而在 Seth Lloyd 模型中，配经典图灵机只可以解决 $BPP_{path}$ ，配量子图灵机可以解决 PP。

F.我们熟知的神经网络.前提是具有无限精度，然而现实中不可能做到，因为现实中存在热力学制约和量子基本单位的制约。

G.无限时间图灵机. 由 Joel Hamkins 和 Andy Lewis 提出。作为芝诺机的泛化模型，可以在离散时间内执行超限数计算步骤（例如 $\omega$ . $\omega$ +1...2 $\omega$ ... $\omega ^{2}$ ... $\omega ^{\omega }$ ... $\varepsilon _{0}$ ...）。在限定的超限序数时间内, 计算机的组态是根据所有之前的组态定义的。当机器进入一个特殊的极限状态（limit-state）时,操作带的方格将取其如下数值：

0, if the square has settled down to 0
1, if the square has settled down to 1
1, if the square alternates between 0 and 1 unboundedly often

读写头被放回第一个操作带方格上, 然后机器从这个极限状态继续它的计算。如果在某一时刻没有 appropriate step 来执行，则该机器停机。因此, 它可以在有限的计算步骤内停机, 或无限计算步骤内停机, 或继续在超限序数时间内运行, 永不停机。

无限时间图灵机可以用 $\omega$ 步骤来计算任何递归可枚举函数, 通过将其操作带上的第一个方格设置为 0, 然后开始计算函数。如果 f（n）=1 ，则第一方格字符再设置为1。具体地，如果 f（n）=1，经过 $\omega$ 步骤计算后其第一方格数值保留为1；如果 f（n）=0，经过 $\omega$ 步骤计算后其第一方格数值保留为0。类似的方法也计算任何递归可枚举实数。由于无限时间图灵机在计算过程中可以使用它们的全部方格, 因此，它们接受无限输入时 , 也可以产生无限输出。

无限时间图灵机是图灵机计算时间延长至超限序数的自然延伸。该模型需要在完全连续的（不存在最小时间单位）的时间里进行计算，然而在现实中不可能做到，因为这样该机的读写头的速度会违背相对论速度极限。

H.模糊图灵机.（Fuzzy Turing Machine）

模糊图灵机会采用基于模糊逻辑的模糊算法，可以在“不经意间”解决经典图灵机不能解决的“停机问题”，由 Wiedermann 提出并证明了该类型图灵机可以解决不可判定问题，允许非递归函数的计算。模糊图灵机的形式七元组是一个模糊系统 $M=(Q,\Sigma ,\Gamma ,\delta ,q_{0},B.F )$ ,其中 $Q,\Sigma ,q_{0} ,\Gamma$ 的定义与经典图灵机的定义一致， $\delta$ 为 $Q*\Gamma *Q*\Gamma*\left\{ L,R \right\}$ 的模糊子集，即函数 $\delta$ ： $Q*\Gamma$ * $Q*\Gamma *\left\{ L,R \right\} \rightarrow \left[ 0,1 \right]$ 表示模糊转移函数，F为Q的模糊子集，表示模糊终状态或模糊接受状态。

模糊图灵机的计算本身只要求一个大概的分布，而不要求精确值。精确并不是必须的，从而整个计算过程并不要求离散化，至少对输入不作要求，只要在输出的时候离散化到某几个特定范畴。这样的话，由于计算精度要求带来的约束就可以放宽。

I.广义相对论中的 Malament-Hogarth 时空。

这些时空拥有一条奇怪的世界线，世界线的本征时间（proper time）是无限的，但时空中存在一个 event p ，沿着世界线发生的所有事件都可以包涵于 event p 中的过去有限区间中。这个 event p 称为 Malament-Hogarth event 。

一个标准的 Malament-Hogarth 时空模型是这样的：

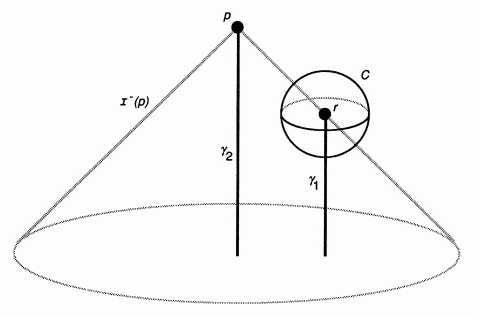
首先，在 Minkwski 时空 $\left( \Re ^{4} ,\eta _{ab} \right)$ ，考虑一个紧致集（compact set）C 且 $C\subset M$ ；选定一个位于 M 上的标量场（scalar field）Ω ，位于紧致集 C 之外且 Ω=1；时空中存在一个 point r 属于紧致集 C，在接近 point r 时，Ω 迅速变为无限。

则时空 $\left( \Re ^{4} -r,\Omega ^{2} \eta _{ab} \right)$ 是一个 Malament-Hogarth 时空。

时空中的任何类时曲线在接近 point r 时本征时间将变为无限（图中的 $\gamma _{1}$ ），而一条类时曲线在接近时空的 endpoint p 时则它的本征时间却是有限的（图中的 $\gamma _{2}$ ），而在 $\gamma _{1}$ 上发生的所有事件都已经成为过去。

即：在时空 $\left( M,g \right)$ 中，M 为连贯四维豪斯多夫 $C^{\infty }$ 流形，g 为洛伦兹度规：

I. 如果存在类时半曲线（timelike half-curve） $\gamma _{1} \subset M$ ；

II.存在一个 event point p，其中：

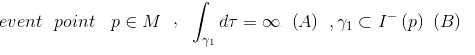
其中（B）表示为 p 的过去区间。则它为 Malament-Hogarth 时空。此外：

还存在一条未来定向类时半曲线 ( future-directed timelike half curve) ：

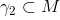
III.存在一个 event point q ，其中：

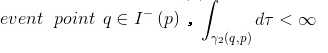
于是有了以下的提议：

让一台计算机（图灵机）沿着类时曲线 $\gamma _{1}$ 移动，由于它的本征时间是无限的，图灵机就有时间来进行无限步骤的计算过程。而一个观测者则沿着类时曲线 $\gamma _{2}$ 移动，时间是有限的，当观测者到达 p 时，图灵机的无限计算也已经完成了。

更正一下，Malament-Hogarth 时空不是单一的时空结构，事实上它是一类特殊时空结构的统称。

它们包括：

I. anti-de Sitter 时空

II. Reissner-Nordström 时空（RN 黑洞中）

III.Kerr-Newman 时空（克尔-纽曼黑洞中）

IV.一个"卷起来"的 Minkowski 时空（补充说明，该 Malament-Hogarth 时空中的时间维被卷了起来，形成封闭类时曲线。）

这些时空相当于是把Malament-Hogarth 时空塑造成一台时空版的无限机器。使得计算机器任意的无限枚举都可以在一个常数时间内完成。

Malament-Hogarth 时空的时空结构允许超计算能力逐级递增，利用这些时空结构，

数学家 Mark Hogarth 把 Malament-Hogarth 时空构造成一个叫 SAD -计算机（SAD machine）的非图灵计算机，它们各部分依次能判定不可解度不同的集合。

简要地讲，在 Malament-Hogarth 时空中进行操作， $\gamma_{1}$ 为无限图灵机， $\gamma _{2}$ 为观测者。

它可以判定任何的任一如下关系形式：

$S(z)= \exists xR\left( x,z \right)$ 或者 $S\left( z \right) = \forall xR\left( x,z \right)$ ，其中 R 是递归关系。上述方式就相当于构造了一台 $SAD_{1}$ 计算机。一台时空版的芝诺机。

在 Malament-Hogarth 时空的操作区域为 $O_{i} ,i=1,2,3,...n$ ，则：

I. $O_{i} \subset I^{-} \left( O_{i+1} \right)$ ；

II. $O_{i } \subset I^{-} \left( p \right)$ 。

在 Malament-Hogarth 时空区域中重复 $SAD_{1}$ 操作， $\gamma _{1}$ 为一台无限图灵机来判定 $\forall yR(i,y)$ ,

然后另外一台无限图灵机来收集各部分结果判定 $\exists x\forall yR(x,y)$ 。 $\gamma _{2}$ 为观测者，收集结果。

最终构造了 $SAD_{2}$ 计算机。它可以判定：

$S_{2} \left( x_{3} \right) =\forall x_{}\exists yR\left( x,y \right) =\forall x_{1} \exists x_{2} R\left( x_{1} ,x_{2} ,x_{3} \right)$

或者

$S_{2}^{'}\left ( x_{3} \right )=\exists x\forall yR\left ( x,y \right )=\exists x_{1}\forall x_{2}R\left ( x_{1} ,x_{2},x_{3}\right )$

重复 $SAD_{2}$ 操作，得到 $SAD_{3}$ 计算机；重复 $SAD_{3}$ 操作，得到 $SAD_{4}$ 计算机 ........

最终，重复所有的操作后。可得到如下递归关系：

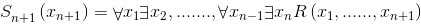
或

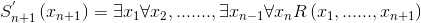
于是，我们得到了一台 $SAD_{n}$ 时空计算机.

在 $SAD_{n}$ 时空中：

I.当 n=1时，为 Malament-Hogarth 时空；

II. 当 n >1 时， $SAD_{n}$ 时空计算机由 i 台 $SAD_{n-1}$ 计算机“串联”构成；

III. $SAD_{1}$ 计算机可以判定克林算数层级中的 $\Sigma _{1}^{0} \cup \Pi _{1}^{0}$ 层级； $SAD_{2}$ 计算机可以判定 $\Sigma _{2}^{0} \cup \Pi _{2}^{0}$ 层级； $SAD_{3}$ 计算机可以判定 $\Sigma _{3}^{0} \cup \Pi _{3}^{0}$ 层级； .......而最终 $SAD_{n}$ 计算机可以判定 $\Sigma _{n }^{0} \cup \Pi _{n}^{0}$ 层级。

通过这样操作, SAD-计算机的计算能力可以覆盖完整的克林算数层级。使其计算能力达到

Hyperarithmetical。

最终，把所有操作全部 "串连" 在一起。相当于构造了 AD ( Arithmetical sentence deciding ) machine。

AD machine 可以精确地求解 $\aleph _{0}$ 函数和判定 Arithmetic 。

P.S. 对 Kerr 时空进行操作步骤如图所示：

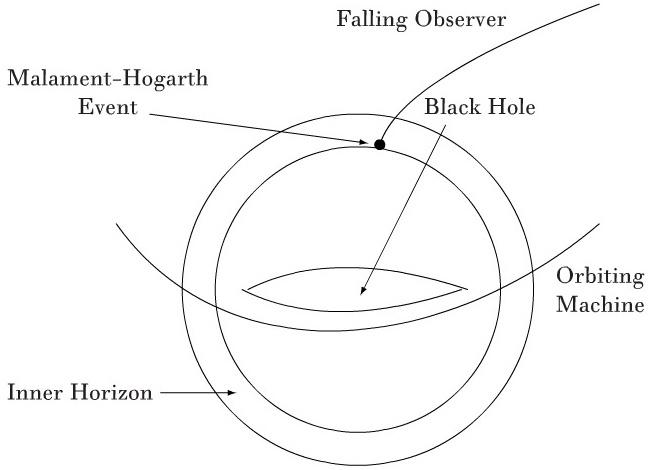
首先，对黑洞时空世界线（位于克尔-纽曼黑洞的赤道平面的轨道）运行的图灵机（Orbiting Machine）进行设置计算任务。

接着，图灵机开始无穷无尽的计算任务。计算任务的计算步骤与计算时间为无限。计算机将会经历无限数量于观测者的本征时间。

然后，观测者（操作人员）（Falling Observer）进入 Malament-Hogarth event ，“图灵无限计算任务”这一事件在 Malament-Hogarth event 的有限时间内被观测者（操作人员）所经过。（观测者的这一路径只会用掉有限的本征时间。）

接着，观测者穿过 Malament-Hogarth event 并从内视界离开黑洞，最终观测者离开黑洞时，图灵机的无限计算任务也已经完成。在观测者的参考系来看就相当于是图灵机在有限时间内完成了无限多次的计算步骤。

最后，在图灵机确认完成计算任务（停机）后发送计算结果给观测者，观测者收到计算结果后，（操作人员）发出终止指令。计算完成。

Malament-Hogarth 时空具体可以干些什么呢？

答：如果 Malament-Hogarth 时空存在且计算操作可以实现，则它可以实现超级任务（Supertask）！

超级任务（Supertask），是芝诺悖论的现代变体。指的是有限时间内完成无限多次操作序列的任务。比如说 π 的最后一位数字；汤姆逊灯；等等。

完成该任务的机器称为 infinite machine 。

目前主流的认识是：超级任务是不可能完成的， infinite machine 不存在。

不过，在 Malament-Hogarth 时空中，在有限时间内完成无限多次操作的过程，理论上是可以完成的。

J.芝诺机.该模型使用 $\frac{1}{2^{n} }$ 的时间来完成算法的第n步。可以在有限的时间内完成无限的运算步骤。举个例子，一种算法第一步需要0.5s，第二步需要0.25s，第三步需要0.125s，...在1秒钟之后，这段无穷步骤的算法就可以完成。

另外经典图灵机的“停机问题”就可以在芝诺机上由如下的算法给出解答：

begin program
  write 0 on the first position of the output tape;
  begin loop
    simulate 1 successive step of the given Turing machine on the given input;
    if the Turing machine has halted, then write 1 on the first position of the output tape and break out of loop;
  end loop
end program

该算法的另一种形式：

begin 
write 1 to the first cell of the tape (output)
 i ← 1
 while i > 0 do
    run given TM m for given input n for i steps 
         if m halts then
            write 0 to the first cell of the tape
            i ← i + 1 
         end if 
    end while
 end

P.S.该模型同样需要可以无限分割的时间，同时保证计算机器的计算步骤可以无限的加速。可惜我们的宇宙中造不出这样的计算机器。

虽然在量子理论的普朗克时间限制和相对论的光速限制下物理不允许这样的机器出现在现实世界。但是，在现有的理论，比如广义相对论，或许允许我们利用特殊的时空结构以另外一种方式——"计算机的无限计算步骤可以在另一个观察者有限的本征时间内完成"来达到同样的效果，即 Malament-Hogarth 时空。

K.Fast-growing constructs Oracle.

Dmytro Taranovsky 提出了一个传统非有限分析分支的有限模型，围绕一个配备一个具有以不可计算速率快速增加功能的增长函数作为谕示的图灵机，能够给出一个二阶算术的解答。

L.Fair nondeterminism .

曾有提议一种叫Fair nondeterminism 或Unbounded nondeterminism 的技术可能允许不可计算函数的计算.不过至今对此存在质疑。我们需要访问一些可以直接实现 Fair nondeterminism 的物理过程。最有前途实现的物理途径似乎是量子力学。但量子计算的标准模型不允许的任何非递归计算函数，而是使用非决定论的形式来进行加速计算（也就是量子计算机）。所以，目前尚未找到任何一种物理方法可以实现它。

M.实计算机（Real computer）.和Blum–Shub–Smale machine一样可以对无限精度的实数进行实际计算的计算机。它的计算能力允许在多项式时间内解决NP完全问题甚至是Sharp-P （#P）完全问题。这是在 Real computer 可以计算可计算的实数的情况下的结果。

当然，Real computer 也可以进行 hypercomputation 并判定图灵停机问题，当 Real computer对所有实数进行计算时可得此结果。前提是物理上允许无限精度实数的存在，并且需要能够将对真实物理值测量为任意精度的能力。

N.极限递归.由Gold提出的极限递归理论中图灵停机问题可以在一个有限时间里得到判定结果，不过我们不能知道这个结果在确切何时取得，于是大部分学者认为在无限长时间后才能取得结果。

O.演化计算机. 该模型对应着一个可以能够进行自我复制和随机调整其结构的计算系统，该系统可以和生物一样也能够演化，并产生适应环境的特征。如果该计算系统所对应的初始状态和随机变量概率分布函数是图灵不可计算的，则它可能在常数时间内演化出可以解决停机问题的个体。

（实验.Evolving digital ecological networks，wikipedia）

P.波计算机. 在物理学家费曼的演讲《The Character of Physical Law》中提及，对于物理现象的计算机仿真时，即使做了全面离散化也不保证仿真的有效性，从而所谓有限自然假说的初衷无法满足。在实数域上可以存在无限多不可计算的连续函数，并且求导和积分不保持可计算性。那么描述某个物理体系的微分方程完全可以有一个不可计算的解，不满足“总能用有限步运算逼近到充分的精度”的条件。上世纪80年代，文献 Advances in mathematics 39,215-239（1981）中就证明了：可以用机械波构造出了初始条件可计算，但解一般不可计算的一个范例。曾被提议制造利用机械波为计算介质进行超计算的波计算机。

P.S. 在上述论文中，机械波的存在遵循着三维波动方程（wave equation）：

$\frac{\partial^2 u}{d x^{2}}+\frac{\partial^2 u}{\partial y^2}+\frac{\partial^2u }{\partial z^2}-\frac{\partial^2u }{\partial t^2}=0$

而为了使该波动方程具有唯一的解，这个唯一解 u 将由两个初始条件（initial conditions）所决定：

当 t = 0 时： $\frac{\partial u}{\partial t}\left( x,y,z,0 \right)=0$ 和 $u\left( x,y,z,0 \right)$

而初始条件可由一个图灵可计算函数 f 所对应： $u\left( x,y,z,0 \right)=f\left( x,y,z \right)$

但在 t 时刻后，f 在波动方程中的解 $u\left( x,y,z,t \right)$ 不可计算，且该解的数值 $u\left( 0,0,0,1 \right)$ 是一个不可计算的实数。

Q.超递归算法（Super-recursive algorithm）.由Mark Burgin提出，并在此基础上提出好几种新的计算模型（例如Gold提出的极限递归就是其中之一。）。他的论述依赖于对算法更广泛的定义，这种定义上的扩展使得一些归纳性图灵机包含的不可计算函数变得可计算。并且Mark Burgin相信他的超递归算法理论可用于反证丘奇-图灵论题。不过这种对邱奇-图灵论题的解读与计算机科学的常规解读不同，把超递归算法归于邱奇-图灵意义上的算法的这种看法并未受到计算领域的广泛接受。

R.量子引力计算机

著名的数学物理学家罗杰·彭罗斯 ( Roger Penrose ) 走出了更加大胆的一步，他推测量子引力不可能用普通计算机或者量子计算机来模拟，即使有可以任你处置的无限的时间和内存。彭罗斯认为应把模拟量子引力的问题归入逻辑学家阿兰.图灵( Alan Turing )和库尔特·科德尔( Kurt Godel )在1930年代所研究的一类问题中，这些问题里有的比 NP 完全问题还要难解--比如确定一个给定的计算机程序是否会停止运行的问题( 比如说“停机问题” )。

最新的量子引力学的进展好像支持一个相反的结论，即它们暗示一台标准的量子计算机甚至可以模拟量子引力过程，比如黑洞的形成与消失。最值得一提的是源自弦理论的 Ads/CFT 对偶，它断定了两种看起来极为不同的理论之间的“对偶性”。对偶的一边是反德西特空间( Anti de Sitter )理论:它是关于一个假想宇宙的一个理论，这个假想宇宙有一个负的宇宙常数，它导致整个宇宙被一个反射边界所包围。而另一边则是共场理论( Conformal Field Theory ):一个没有引力，只存在于 AdS 空间的边界上的“普通”量子场理论。Ads/CFT 对偶原理已有压倒性的(虽非确凿的)证据指出，任何关于在 AdS 空间中是什么情况的问题都可以转化为关于 CFT 的一个“相当的”问题，反之亦然。

这就意味着，如果我们想在AdS空间中模拟量子引力现象，我们就可能可以先把这个问题转化到CFT 那一边，然后在量子计算机中模拟这个 CFT ，最后再将结果转化回 AdS 中。这其中最关键的一点是，因为 CFT 不包括引力，在量子计算机中模拟它的难度就“仅仅”是相对简单的如何在量子计算机中模拟量子场论的问题。更广义地说，我们能从 AdS/CFT 中所了解到的是，即便量子引力论看起来“疯狂”--即使它包括了非定域性、虫洞及其他的新奇事物--它也可能有一个更加“驯服”的与之对偶的叙述方式。(要让这成为可能， AdS 与 CFT 描述之间的转化需要在计算上是高效的--也有可能有些情形下它没办法高效。)

S. Asynchronous Networks of Turing Machines

虽然拥有信息网络的图灵机群的能力与单一图灵机等价。不过这一结果只在 synchronous networks 中成立。在文献 “Beyond the Universal Turing Machine” 中，Copeland 和 Sylvan 探讨了 Asynchronous Networks ，其中每一个图灵机使用一个定时函数（timing function）： $\Delta _{k} :N\rightarrow N$ 代表执行 $n^{th}$ 处理与执行 $\left( n+1 \right) ^{th}$ 处理之间的时间间隔。如果两台计算机器在同一条操作带上运行这个定时函数，则它们可以判定图灵停机函数（停机问题）。

T. Error Prone Turing Machines

这个模型是作为 unharnessable hypercomputation 的自然拓展。该模型经常会有意输出一个不同的符号，即会故意出错。对于字母表只有0与1的图灵机来说，输出一个错误符号仅仅意味着在1的位置输出0或反之亦然。

在 Error Prone Turing Machines 中这种错误行为可以定义为由于误差函数（error function）， $e:N \rightarrow \left\{ 0,1 \right\}$ 在机器写入其错误的 $n^{th}$ 符号的情况下当且仅当 $e\left( n \right) =1$ 。这类模型可以利用 error function 来判定停机函数和其他的非递归函数。

U.Coupled Turing Machines

该模型也由 Copeland 和 Sylvan 提出。这是在计算过程中拥有一个或多个输入通道来提供输入的计算模型。这一输入可以以机器的字母表中的一个符号的形式写在机器的操作带的第一个方格上。这个方格是为特殊的输入而保留，不能由读写头写入。与谕示机一样, 特定的输入序列决定了 Coupled Turing Machines 可以执行的功能。例如，如果模型有一个又一个的 $\tau$ 位输入，则该模型可以计算所有其他的递归可枚举函数。

V.量子模型.

在计算理论历史上，也有人提出过量子版本的 hypercomputation 模型。

1990年，Norton 探讨了 Supertask 在量子领域实现的可能性。他考虑了一个具有无限晶格点阵（Infinite lattice）的交互谐振子（Harmonic oscillators）系统。如下图所示：

Norton 假设每两个谐振子之间的 spring 都具有相同张力以及相同的系统运动方程解，Norton 发现它可以自发地在有限的时间内产生无限连续的振荡。利用这个系统作为模型, Norton 制造了一个类似 Supertask 的谐振子量子晶格点阵。

以一个无限晶格点阵的 2 维量子系统作起始，其每一个谐振子都具有一个基态 | $\phi$ ⟩ 和一个激发态 | $\chi$ ⟩ 。考虑其向量集（Collection of vectors）：

......

之后 Norton 得到了这交互系统薛定谔方程的微分形式：

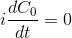
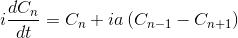
Norton 争辩说, 他的解决方案中在无限晶格中的所有节点开始由基态转变为激发态的时间是有限的。

Norton 的量子 Supertask 需要一个非标准（Non-standard）的量子系统，因为他所提出的动力学演化不是单一的, 即使它服从一个微分方程形式的薛定谔方程的波函数空间中。

W. 量子模型二.

如果我们不断地监控一个量子系统, 比如一个不稳定的原子, 会发生什么？预测的效果是系统不会改变, 即使它是一个不稳定的原子，也会迅速衰变。

1977年，Misra 和 Sudarshan 提出对一个芝诺式 supertask 的系统进行“精确监测”。假设一个不稳定的原子是根据某种幺正演化定律（law of unitary evolution ） $U_{t}$ 而演化的。假设我们衡量的原子是否已经发生衰变是遵循芝诺二分法的回归形式。即我们在时间 $t$ 进行测量；而后在时间 $\frac{t}{2}$ 进行测量；接着在时间 $\frac{t}{4}$ 进行测量，等等。让 $E$ 为粒子初始未衰变状态的射影（projection）。在 supertask 的每个阶段找到原子未衰变阶段然后对应于每个序列：

$EU_{\frac{t}{2^{-n}}}E,\left (n \geq 0 \right )$

Misra 和 Sudarshan 使用此序列作为一种模型进行连续测量，假设上面的序列收敛于一个算子： $T\left ( t \right )=E$ 而这样做的所有时间大于或等于零。然后在固定时间 t=0 对原子进行连续观测。他们从这个假设证明, 对于大多数合理的量子系统, 如果初始状态在 $Tr\left ( \rho E \right )=1$ 的意义上是未衰变的，那么原子在任意给定时间间隔 $\left [ 0,1 \right ]$ 中衰变的概率等于零。也就是说, 持续的监测意味着原子不会衰变。

也就是说，如果我们可以连续地测量一个不稳定原子以观察它是否仍然处于初始状态，则始终能发现该原子处于初始状态。

这个提议引发了大量的反响。Ghirardi 等人和 Pati 反对这样的芝诺式量子测量模型，因为它与量子理论的其他特征，如时间-能量不确定关系（time-energy uncertainty relations）相抵触。不过 Bokulish 认为，这种 Supertask 仍然可以进行，当对易测量（measurement commutes）呈幺正演化（例如 E 为能量本征态的投影。）。

物理学家 Deutsch 所设想的 “终极超计算模型” ，即存在一台可以仿真所有其他物理系统的通用仿真机。这是一个未定的假说：CTD原理（Church–Turing–Deutsch principle ）。如果该论题为真，那么计算机的计算能力一定是存在上限的，虽然说上限不一定是图灵机。

除此之外，超计算模型还有很多很多，例如概率图灵机，无限状态图灵机，等等等等。这里不再一一列举了。

P.S. 这里的的超计算模型介绍是不太严谨的，如有错误，请多包涵。仅仅是高度科普高度口水化的介绍。

不过，对于任何一台谕示机，无论所带谕示的谕示能力多么强大，都存在其自身谕示不能判定，必须由更高一阶的谕示机才能判定的停机问题。通过添加能力越来越强的“谕示”来让经典图灵机不断突破计算能力限制，而谕示机的停机问题的层级为原先谕示机的层级的图灵跳跃（Turing jump），是一种顺序关系，于是得到一个 $0^{\left( n \right) }$ n为超穷序数的超穷层级，称为图灵度层级（不可解度）。

经典图灵机可以计算的可判定问题位于最最底层，是最最简单的层级，记作0。

除了0以外的全部层级都是不可计算的不可判定问题。而且层级越高，问题越难。

从经典图灵机的层级0出发，经过一次图灵跳跃得到 $0^{'}$ ；即图灵停机问题所在的图灵度。经过二次图灵跳跃得到 $0^{''}$ ；即可以判定图灵停机问题的谕示机的停机问题的图灵度，以此类推。

另外，在一个关于自然数的逻辑公式P(x)中，只有一个自由变元x，那么，使这个公式成立的所有值组成的集合为P(x)定义的自然数集。在这其中没有量词的命题被称为零阶命题，而有量词的命题，它们开头必定由存在量词和全称量词交错组成，这样交错的段数，就是命题的阶数。对于一个n阶命题，如果它的开头是存在量词，我们就称它为n阶存在命题，反之则是n阶全称命题。

在这些这些类别的命题能定义的自然数集中，0阶命题定义的自然数集组成的集合称为 $\Delta _{0}$ ，而将n阶存在命题和n阶全称命题定义的自然数集组成的集合分别称为 $\Sigma _{n}$ 和 $\Pi _{n}$ ，这些集合组成了一个向上无限绵延的层级，每一层都是自然数集组成的集合，阶数越高，命题能定义的自然数集也越多，表达能力也越强。对于每一层，总有存在这样的集合，它只能被这一层及以上的命题定义，而不能被下方更弱的层定义。这就是除了图灵度以外可以判定一个计算机器计算能力的另一个层级：克林算数层级（Kleene arithmetical hierarchy）。

部分 Hypercomputation 计算能力比较：

经典图灵机： $\Delta _{0}^{0} \left( =\Delta _{1}^{0} \right)$ ；芝诺机： $\Sigma _{1}^{0}$ ；模糊图灵机： $\Sigma _{1}^{0} \cup \Pi _{1}^{0}$ ；

Malament-Hogarth 时空（SAD machine）： $\Sigma _{n }^{0} \cup \Pi _{n }^{0}$ ，（等价于 $\Delta _{1}^{1}$ ）。

无限时间图灵机：介于 $\Sigma _{1}^{1} \cup\Pi _{1}^{1}$ 和 $\Delta _{2}^{1}$ 之间；

无限状态图灵机：ALL （超过整个算数层级）；

Fair nondeterminism 谕示： $\Sigma _{1}^{0}$ ；Dmytro Taranovsky 谕示： $\Delta _{1}^{1} \rightarrow\left( \Sigma_{n}^{1}\cup \Pi_{n}^{1} \right)$ 。

Asynchronous Networks ： recursive timing functions 计算能力与图灵机等价，但使用 arbitrary timing functions 可以判定 ALL 。

至于基于超算模型的计算机能否在我们的宇宙中制造，也就是超计算的物理实现可能性，我们目前无法得知，因为：

1.我们宇宙可能会受到“图灵-丘奇”论题的制约，如果该论题在我们的宇宙中成立，那么超计算在我们的宇宙中就无法实行，就目前来说，我们能实际运用的计算模型都严格等价于经典图灵机。

2.我们的宇宙计算能力存在的布莱梅曼极限（Bremermann's limit）。

3.贝肯斯坦界限（Bekenstein Bound）：量子物理框架下一个质量为 m 半径为 R 的球体所能储存的最多信息量为 $\frac{2\pi cRm}{\hbar ln2}$ bits 。该上限使得真正处理实数的计算机（如 Blum–Shub–Smale machine 和 Real computer）不可实现，即便是在没有热噪声的假想环境里也不例外。

4.热力学极限和相对论极限，使得无限神经网络和芝诺机不可实现。

5.目前在所有的 Hypercomputation 模型中绝大部分都只是只能在数学上成立的"数学机器"，在物理上是无法实现的。

不过并不是所有的超计算模型都只能在数学上存在，已经有部分模型在物理上找到了对应对象。

它们的实现在物理上是可能的。

不过这些模型学术界对它们是否能真正地在物理上突破图灵屏障至今存在质疑和争议。比如说：

I.SAD machine 所需要的 Malament-Hogarth 时空只是单纯在广义相对论框架下得出的结果，并未考虑量子引力。而且在 Malament-Hogarth 时空中，未来并不是完全地由当前的时空来决定。

II.即使在现实的物理中 Malament-Hogarth 时空确实存在。那利用它进行超图灵计算之前还得克服一个问题：计算机中的热噪音。要让 Malament-Hogarth 时空的超计算确实可行，计算机中就不能存在热噪音。因为 Malament-Hogarth 时空中的蓝移问题会导致其噪音被放大而掩盖通讯信号。而计算机为抵抗噪音造成的耗散不可避免，这将导致计算机需要无限大的能量维持运作，这是非常不现实的。

III.封闭类时曲线计算机所需要的可以进行时间旅行的类时闭曲线时空的特殊时空结构在数学上是可能的。但如果在正能量条件普世的条件下现实的物理系统就不允许它的出现和存在。著名数学家丘成桐就曾证明遵循正能量条件的时空中就不存在封闭类时曲线。最直接的让其存在最有效的方案，就是放弃正能量条件，也就是说让自然规律允许负能量的物质出现。

IV.封闭类时曲线计算机可以明确的计算能力的问题判定范围是全部 PSPACE 。即使用一个 Polynomial - size 字符串，封闭类时曲线计算机可以在多项式时间内准确判定 PSPACE。但有学者认为还存在一个（在 Unbounded case 情况下）达到了图灵不可计算问题的级别（准确地说是 $\Delta _{2}^{0}$ 的级别）；也就是说封闭类时曲线计算机的计算能力不仅可以解决全部的 PSPACE，还存在可以判定图灵机的停机问题的可能。

不过这不代表它真的就"一定可以解决" 。因为这需要任意长度字符串的计算在封闭类时曲线中得到允许（这代表需要无限宽的输入通道）才有可能真正做到。

其次因为面对这类不可计算问题时，封闭类时曲线计算机所拥有的符合自治性结果将不再唯一；面对自治性结果不唯一的情况时，大自然将会让封闭类时曲线计算机从所有的自治性结果中选择令整体冯·诺依曼熵最大的结果。不过这是一个坏消息，因为直觉上计算机的电路板被烧穿，整个机器崩溃会带来更高的冯·诺依曼熵。

所以，当封闭类时曲线计算机在运行图灵不可计算问题时，面对"机器崩溃，直接坏掉。"和"吐出该问题的判定结果。"的选择可能性时，封闭类时曲线计算机更有可能会选择前者......

V.波计算机所利用的不可计算机械波，就是通过构造了一个可计算函数，其导数是非递归不可计算函数。再对其结果进行扩展，构造出一组特殊的偏微分方程，在某个特定的初始值下，某个时刻 t 后的解不可计算。但该偏微分方程组可作为某个物理系统的演化函数。这个系统理论上可以以机械波进行对应。当然，这个系统是否可以利用人为实验构造出来就另当别论了

如果宇宙不是一台图灵机。

正如费曼在他的演讲中所表达的困惑，一个描述某个物理体系的微分方程完全可以有一个不可计算的解，不满足“总能用有限步运算逼近到充分的精度”的条件。换言之，有效的数值解都不会存在（更不用说解析解了）。这种体系更符合费曼原文描述的情况：似乎我们非得用“无限的逻辑”才能理解“有限的时空”中的演化，即使做了近似也帮不上多大忙。
引用恩里科·费米的一句话：

圣经中并没有说过一切大自然的定律都可以用线性方程来表示。

引用费米的话以强调非线性研究的人可能会非常看重数值计算的作用，经验告诉他们，面对没有解析解的非线性方程，数值近似是有力的武器——但是那同时也就不知不觉假设了算法可解性，一个同样是“圣经里”没有的假设。

再加上目前已经构造出了机械波这一不可计算物理现象的范例。是否可以说，存在着一部分物理体系，它们无法用图灵机的有限步运算步骤进行模拟和重现，即不可计算的物理现象。也就是说，物理定律不是图灵可计算的。

同理，用于构造不可计算机械波的方式，说明理论上我们可以通过构造出一个物理系统，让其演化出的物理系统可以计算一个图灵不可计算函数。理论上超越图灵机的函数在物理上是可以存在的。

另外，如果我们的万物理论（Theory of everything）是基于弦理论的 M-theory 的话，会有一个不可思议的结果：M-theory 具有 T-对偶性（T-duality），采用弦论把一个维度包进一个半径为 R 的圆圈中，在采用另外一个弦论把一个维度包进一个半径为 1/R 的圆圈中，两者对比会发现，完全一样。

即使让 R 变得非常小，甚至小于普朗克长度，也成立。因为在普朗克尺度时空会呈现出泡沫状，而远大于和远小于普朗克尺度的时空则会是平滑的，二者完全一致。如果它最终是正确的，也就意味着，即使目前的物理给出了一个最小距离：普朗克长度，物理也并不以普朗克长度而戛然终止。弦论最小的普朗克距离以内，也可以有一个完整的宇宙。在大大小于普朗克距离内，我们也可以利用场论而非数字化结构来描述整个宇宙。从这点看，宇宙也不是一台图灵机，物理系统也不是一个计算机程序。

既然物理理论上允许不可计算的现象存在，在最乐观的情况下，可以用于制造突破现有计算设备根本限制,不受丘奇-图灵论题约束的强力装置：超计算机（Hypercomputer），完成跨越图灵屏障（Turing's barrier）。做到：

1.由不可计算的物理现象构成的Hypercomputer至少可以帮助我们完成一个经典图灵机做不好的任务：仿真它自己。因为经典图灵机的有限步运算无法给出有界连续变量的大多数取值，只能做近似模拟。而且不可计算性会导致初始条件精确已知时依然难以做长期预测，而可计算的混沌则会失去作用。单纯的混沌现象在不可计算现象面前根本就是小巫见大巫

2.Hypercomputer可以帮助我们访问图灵机不能访问的更高阶层的arithmetical hierarchy和degrees of unsolvability。解决图灵机不可判定问题。

3.Hypercomputer可以用来构建非递归枚举的形式系统。最重要的是，非递归枚举形式系统不受哥德尔不完备性的限制。

P.S.比如说True arithmetic,即把所有在 $(N,0,1,+,*)$ 上成立的一阶语句抽取出来，令数论中的所有真命题组成一个集合，把里面所有的真命题当作公理。这样的形式系统既包涵了皮亚诺公理（足够强），又是自治完备的。自治性与完备性兼得且两不误。那么哥德尔不完备性对它无效。不过我们是没有办法构建这样强大的形式系统的，因为它们对于我们来说是不可计算的。由于它的不可计算性，其次是因为使用图灵机的话我们很可能无法在一个有限时间里获得它的公理（因为它是非可枚举的。）。想要获得非可枚举形式系统中的公理，除非使用超计算。

当然最悲观的可能性就是：这些不可计算现象仍然是不可能利用的。可实行的计算最终还是脱离不了图灵机的能力范围，图灵屏障仍旧无法跨越。那么还有一件事情是很值得做的：弄清楚这种异常背后的原因。

posted @ 2017-11-07 18:29 lsgxeva 阅读(6655) 评论(0) 编辑收藏举报

刷新页面返回顶部

云水

MyGitee - https://gitee.com/lsgx/
MyGithub - https://github.com/lsgxeva/
Download - https://d.serctl.com
Proxy - tcp://frpgz1.idcfengye.com:10000

超计算（Hyper computation）模型

超计算（Hyper computation）模型

公告

云水

MyGitee - https://gitee.com/lsgx/ MyGithub - https://github.com/lsgxeva/ Download - https://d.serctl.com Proxy - tcp://frpgz1.idcfengye.com:10000

超计算（Hyper computation）模型

超计算（Hyper computation）模型

公告

MyGitee - https://gitee.com/lsgx/
MyGithub - https://github.com/lsgxeva/
Download - https://d.serctl.com
Proxy - tcp://frpgz1.idcfengye.com:10000