KAN: Kolmogorov–Arnold Networks 学术论文全译
KAN: Kolmogorov–Arnold Networks 学术论文全译
来源 https://zhuanlan.zhihu.com/p/696001648
KAN: Kolmogorov–Arnold Networks https://arxiv.org/pdf/2404.19756
讨论
Application aspects: We have presented some preliminary evidences that KANs are more effective than MLPs in science-related tasks, e.g., fitting physical equations and PDE solving.
We expect that KANs may also be promising for solving Navier-Stokes equations, density functional theory, or any other tasks that can be formulated as regression or PDE solving.
We would also like to apply KANs to machine-learning-related tasks, which would require integrating KANs into current architectures, e.g., transformers – one may propose “kansformers” which replace MLPs by KANs in transformers.
KAN as a “language model” for AI + Science
目前,KANs 最大的瓶颈在于训练速度较慢。在相同数量的参数下,KANs 通常比 MLPs 慢 10 倍。
老实说,作者并没有努力优化 KANs 的效率,认为 KANs 的训练速度更多地是一个未来需要改进的工程问题,而不是一个基本限制


摘要 (翻译供大家快速参考)
受科尔莫戈洛夫-阿诺尔德表示定理的启发,我们提出科尔莫戈洛夫-阿诺尔德网络(KANs)作为多层感知机(MLPs)的有希望的替代方案。虽然 MLPs 在节点(“神经元”)上具有固定的激活函数,但 KANs 在边缘(“权重”)上具有可学习的激活函数。KANs 没有任何线性权重 - 每个权重参数都被一个作为样条参数化的单变量函数替换。我们展示了这个看似简单的改变使得 KANs 在准确性和可解释性方面优于 MLPs。在准确性方面,较小的 KANs 在数据拟合和 PDE 求解方面可以达到与较大的 MLPs 相媲美或更好的准确性。在理论和实证方面,KANs 拥有比 MLPs 更快的神经扩展定律。在可解释性方面,KANs 可以直观地可视化,并且可以轻松地与人类用户交互。通过数学和物理学中的两个示例,KANs 被证明是有用的“合作者”,帮助科学家(重新)发现数学和物理定律。总之,KANs 是 MLPs 有希望的替代品,为进一步改进依赖于 MLPs 的当今深度学习模型开辟了机会。
1 引言
多层感知机(MLPs)[1, 2, 3],也称为全连接前馈神经网络,是当今深度学习模型的基础构建块。MLPs 的重要性不言而喻,因为它们是机器学习中用于逼近非线性函数的默认模型,其表达能力由普适逼近定理[3]保证。然而,MLPs 是否是我们可以构建的最佳非线性回归器呢?尽管 MLPs 的使用普遍,但它们有着显著的缺点。例如,在变压器[4]中,MLPs 几乎消耗所有非嵌入参数,并且通常在没有后续分析工具[5]的情况下(相对于注意力层)不太可解释。
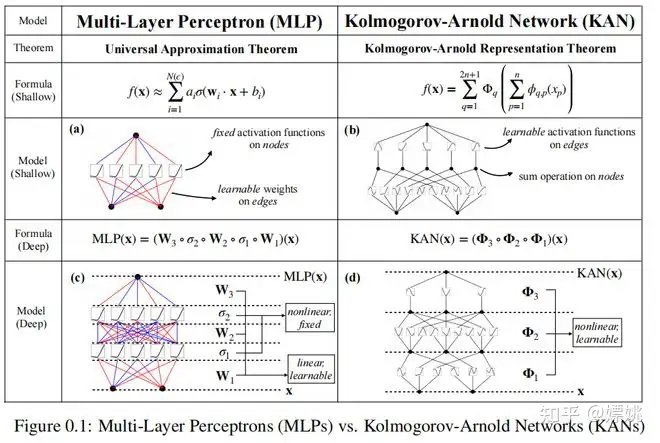
我们提出了 MLPs 的一个有希望的替代方案,称为科尔莫戈洛夫-阿诺德网络(KANs)。虽然 MLPs 受到普适逼近定理的启发,但 KANs 受到科尔莫戈洛夫-阿诺德表示定理[6, 7]的启发。与 MLPs 类似,KANs 具有全连接结构。然而,MLPs 在节点(“神经元”)上放置固定的激活函数,而 KANs 在边缘(“权重”)上放置可学习的激活函数,如图0.1所示。因此,KANs 完全没有线性权重矩阵:相反,每个权重参数都被一个可学习的一维函数替代,作为样条进行参数化。KANs 的节点只是简单地对传入信号进行求和,不应用任何非线性。有人可能担心 KANs 的计算成本过高,因为每个 MLP 的权重参数都变成了 KAN 的样条函数。幸运的是,KANs 通常允许比 MLPs 更小的计算图。例如,我们展示了对于 PDE 求解,一个 2 层宽度为 10 的 KAN 比一个 4 层宽度为 100 的 MLP 精度高 100 倍(10^(-7) vs 10^(-5) 均方误差)并且参数效率高 100 倍(102 vs 104 参数)。
毫不奇怪,利用科尔莫戈洛夫-阿诺德表示定理构建神经网络的可能性已经被研究过[8, 9, 10, 11, 12, 13]。然而,大多数工作都固守原始的深度为 2、宽度为 (2n + 1) 的表示,并且没有机会利用更现代的技术(例如,反向传播)来训练网络。我们的贡献在于将原始的科尔莫戈洛夫-阿诺德表示推广到任意宽度和深度,将其复兴并置于今天的深度学习世界中,并利用广泛的实证实验来突出其作为 AI + 科学基础模型的潜在作用,由于其准确性和可解释性。
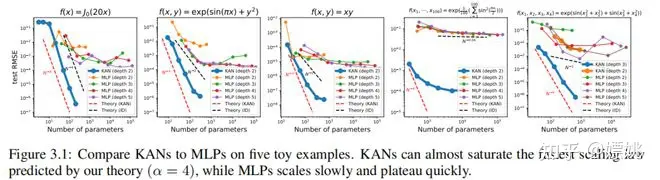
尽管 KANs 具有优雅的数学解释,但它们实质上不过是样条和 MLPs 的组合,利用了它们各自的优势并避免了各自的弱点。样条适用于低维函数,易于在局部进行调整,并能够在不同分辨率之间切换。然而,由于无法利用组合结构,样条存在严重的维度灾难(COD)问题。另一方面,MLPs 由于特征学习,受 COD 的影响较小,但在低维度下精度不如样条,因为无法优化单变量函数。为了准确地学习函数,模型不仅应该学习组合结构(外部自由度),还应该很好地近似单变量函数(内部自由度)。KANs 是这样的模型,因为它们在外部具有 MLPs,在内部具有样条。因此,KANs 不仅可以学习特征(由于它们外部类似于 MLPs),还可以将这些学习到的特征优化到很高的精度(由于它们内部类似于样条)。例如,对于高维函数,样条会因为 COD 而在 N 较大时失败;MLPs 可能可以学习到广义加性结构,但是用 ReLU 激活函数来近似指数函数和正弦函数非常低效。相反,KANs 可以很好地学习组合结构和单变量函数,因此在性能上大幅优于 MLPs(见图 3.1)。

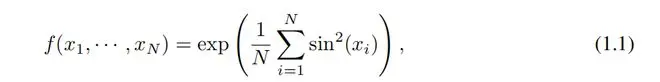
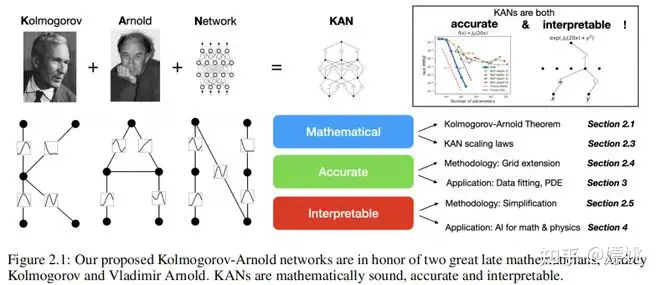
在本文中,我们将使用大量的数值实验来展示 KANs 相对于 MLPs 可以带来显著的准确性和可解释性改进。本文的组织结构如图 2.1 所示。在第 2 节中,我们介绍了 KAN 结构及其数学基础,介绍了网络简化技术以使 KANs 更易解释,并介绍了网格扩展技术以使 KANs 变得更加精确。在第 3 节中,我们展示了 KANs 在数据拟合和 PDE 求解中比 MLPs 更准确:当数据中存在组合结构时,KANs 可以击败维度灾难,实现比 MLPs 更好的缩放规律。在第 4 节中,我们展示了 KANs 具有解释性,并可用于科学发现。我们使用了数学(结扎理论)和物理学(安德森定位)中的两个例子来展示 KANs 可以成为科学家的有益“合作者”,帮助科学家(重新)发现数学和物理定律。第 5 节总结了相关工作。在第 6 节中,我们通过讨论广泛的影响和未来方向来总结。代码可在 https://github.com/KindXiaoming/pykan 找到,并且也可以通过 pip install pykan 安装。
2 柯尔莫哥洛夫-阿诺德网络 (KAN)
多层感知器(MLPs)受到了通用逼近定理的启发。相比之下,我们专注于科尔莫戈洛夫-阿诺尔德表示定理,这可以通过一种称为科尔莫戈洛夫-阿诺尔德网络(KAN)的新型神经网络来实现。我们在第 2.1 节回顾科尔莫戈洛夫-阿诺尔德定理,以启发第 2.2 节中科尔莫戈洛夫-阿诺尔德网络的设计。在第 2.3 节,我们提供了关于 KAN 的表达能力和神经扩展规律的理论保证。在第 2.4 节,我们提出了一种网格扩展技术,以使 KANs 变得越来越准确。在第 2.5 节,我们提出了简化技术,以使 KANs 更易解释。

2.1 柯尔莫哥洛夫-阿诺德表示定理
弗拉基米尔·阿诺尔德(Vladimir Arnold)和安德烈·科尔莫戈洛夫(Andrey Kolmogorov)证明了,如果 f 是定义在有界域上的多变量连续函数,那么 f 可以被写成单变量连续函数的有限组合以及加法的二元运算。更具体地说,对于光滑函数
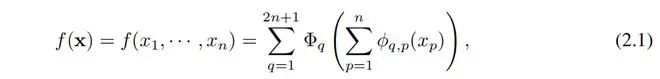
其中 。从某种意义上说,他们证明了唯一真正的多元函数是加法,因为每个其他函数都可以用单变量函数和求和来表示。
有人可能天真地认为这对机器学习是个好消息:学习高维函数归结为学习一系列 1D 函数。然而,这些 1D 函数可能是非光滑甚至是分形的,所以在实践中可能无法学习到它们。由于这种病态行为,科尔莫戈洛夫-阿诺尔德表示定理基本上被判定为在机器学习中理论上合理但实际上无用 [14]。
然而,我们对科尔莫戈洛夫-阿诺尔德定理在机器学习中的用处更加乐观。首先,我们不必局限于原始的方程(2.1),该方程仅具有两层非线性和隐藏层中的少量项(2n + 1):我们将将网络推广到任意宽度和深度。其次,科学和日常生活中的大多数函数通常是光滑的,并具有稀疏的组合结构,潜在地促进了光滑的科尔莫戈洛夫-阿诺尔德表示。这里的哲学与物理学家的思维方式接近,他们通常更关心典型情况而不是最坏情况。毕竟,我们的物理世界和机器学习任务必须具有结构,才能使物理学和机器学习具有任何用处或可推广性[15]。
2.2 KAN架构
假设我们有一个包含输入输出对 的监督学习任务,我们想要找到一个函数 f,使得对于所有数据点都有 。方程(2.1)暗示着如果我们能找到合适的单变量函数 ,那么我们就完成了。这启发我们设计一个神经网络,明确地参数化方程(2.1)。由于要学习的所有函数都是单变量函数,我们可以将每个 1D 函数参数化为 B 样条曲线,其中的局部 B 样条基函数的可学习系数(见图 2.2 右侧)。现在我们有了 KAN 的原型,其计算图由方程(2.1)精确指定,并在图 0.1(b)中示出(输入维度 n = 2),呈现为一个两层神经网络,其激活函数放置在边上而不是节点上(简单的求和操作在节点上执行),并且在中间层具有宽度 2n + 1。
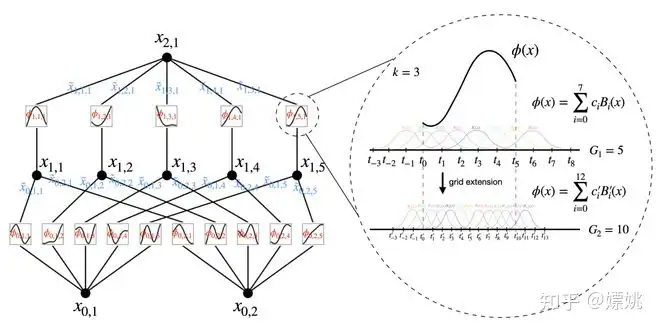
正如前文提到的,实践中已知这样的网络过于简单,无法使用平滑样条任意良好地逼近任何函数!因此,我们将我们的 KAN 推广为更宽更深的结构。如何使 KANs 更深并不是立即清晰的,因为科尔莫哥洛夫-阿诺德表示对应于两层 KANs。
据我们所知,尚不存在与更深的 KANs 对应的“泛化”版本的定理。突破发生在我们注意到 MLPs 和 KANs 之间的类比时。在 MLPs 中,一旦我们定义了一个层(由线性变换和非线性组成),我们可以堆叠更多的层来使网络更深。要构建深度 KANs,我们首先应该回答:“什么是 KAN 层?”事实证明,具有 维输入和 维输出的 KAN 层可以定义为一组 1D 函数的矩阵。
其中,函数 ϕq,p 具有可训练参数,如下所述。在科尔莫哥洛夫-阿诺德定理中,内部函数形成一个 KAN 层,其中 ,而外部函数形成一个 KAN 层,其中 。因此,在方程 (2.1) 中,科尔莫哥洛夫-阿诺德表示简单地由两个 KAN 层的组合构成。现在,深度科尔莫哥洛夫-阿诺德表示的含义变得清晰:只需堆叠更多的 KAN 层!
让我们引入一些符号。这一段会有点技术性,但读者可以参考图 2.2(左)以获得具体示例和直观理解。KAN 的形状由一个整数数组表示。


这里 是对应于第 l 层 KAN 层的函数矩阵。一个一般的 KAN 网络是 L 层的组合:给定一个输入向量 ,KAN 的输出是

我们还可以重新写上述方程,使其更类似于方程(2.1),假设输出维度 ,并定义
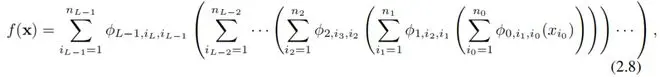
很明显,MLP将线性变换和非线性分别处理为 W 和 σ,而 KAN 将它们整合到 Φ 中。在图 0.1 (c) 和 (d) 中,我们可视化了一个三层 MLP 和一个三层 KAN,以澄清它们之间的区别。
实现细节。虽然 KAN 层方程 (2.5) 看起来非常简单,但要使其具有良好的优化性能并不容易。关键技巧包括:
(1)残差激活函数。我们包含一个基函数 b(x)(类似于残差连接),使得激活函数 ϕ(x) 是基函数 b(x) 和样条函数的和:
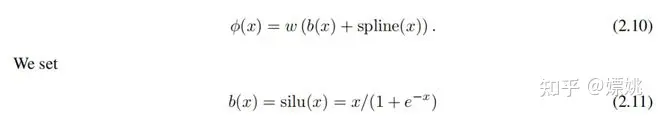
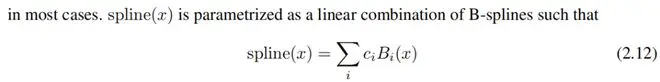
其中 ci 是可训练的。原则上,w 是多余的,因为它可以吸收到 b(x) 和 spline(x) 中。然而,我们仍然包含这个 w 因子来更好地控制激活函数的整体幅度。
(2) 初始化比例。每个激活函数的初始化设置为 spline(x) ≈ 0。w 根据 Xavier 初始化进行初始化,这已经被用于初始化 MLP 中的线性层。
(3) 样条格更新。我们根据其输入激活实时更新每个格点,以解决样条函数在有界区域上定义,但在训练过程中激活值可能会演化出固定区域的问题。
参数计数 为简单起见,让我们假设一个网络
总共有 个参数。相比之下,深度为 L、宽度为 N 的 MLP 只需要 个参数,似乎比 KAN 更高效。
幸运的是,KAN 通常需要比 MLP 更小的 N,这不仅节省了参数,而且实现了更好的泛化(见例如图 3.1 和 3.3),并且有助于解释性。我们用下面的定理来描述 KAN 的泛化行为。

2.3 KAN 的逼近能力和缩放定律
回想一下,在公式(2.1)中,2层宽度为(2n + 1)的表示可能是不平滑的。然而,更深层的表示可能带来更平滑激活函数的优势。例如,4个变量函数
这个函数可以通过一个 [4, 2, 1, 1] 的 KAN 表示,该 KAN 是 3 层的,但可能无法使用平滑的激活函数表示为 2 层的 KAN。为了方便近似分析,我们仍然假设激活函数是平滑的,但允许表示任意宽度和深度,就像公式 (2.7) 中那样。为了强调我们的 KAN 对有限格点集的依赖,我们在下文中使用 来代替公式 (2.5) 和 (2.6) 中使用的符号 。

证明。根据经典的一维 B 样条理论 [19] 以及连续函数 在有界区域上可以一致有界的事实,我们知道存在有限格点 B 样条函数 ,对于任意的 0 ≤ m ≤ k,都有

我们知道,从渐近角度来看,只要定理2.1中的假设成立,有限网格大小的KAN可以很好地逼近函数,其残差率与维度无关,从而打破了维度诅咒!这是很自然的,因为我们只使用样条来逼近一维函数。特别是对于m = 0,我们恢复了L∞范数中的精度,进而提供了有限域上RMSE的界限,这给出了一个尺度指数k + 1。当然,常数C取决于表示方式;因此,它将取决于维度。我们将把常数对维度的依赖性讨论留作未来的工作。
我们注意到,尽管Kolmogorov-Arnold定理(2.1式)对应于形状为[d, 2d + 1, 1]的KAN表示,但其函数未必平滑。另一方面,如果我们能够确定一个平滑的表示(可能要付出额外的层次或使KAN比理论规定更宽),那么定理2.1表明我们可以打破维度诅咒(COD)。这应该不会让人感到惊讶,因为我们可以本质上学习函数的结构,并使我们的有限样本KAN逼近具有可解释性。
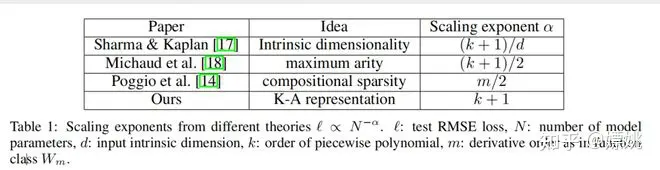
神经缩放定律:与其他理论的比较。神经缩放定律是指随着模型参数的增加,测试损失减少的现象,即 ℓ ∝ N −α,其中 ℓ 是测试 RMSE,N 是参数数量,α 是缩放指数。较大的α意味着通过简单地扩展模型可以获得更多的改进。已经提出了不同的理论来预测α。Sharma & Kaplan [17] 提出α来自于在固有维度d的输入流形上的数据拟合。如果模型函数类别是k阶分段多项式(ReLU的k = 1),那么标准的逼近理论暗示 α = (k + 1)/d。这个界限受到维度诅咒的影响,因此人们试图通过利用组合结构来寻找与d无关的其他界限。特别是,Michaud等人 [18] 考虑了仅涉及一元(例如,平方、正弦、指数)和二元(+ 和 ×)运算的计算图,发现 α = (k + 1)/d∗ = (k + 1)/2,其中d∗ = 2是最大的阶数。Poggio等人 [14] 利用了组合稀疏性的思想,并证明了对于给定的函数类别 Wm(其导数连续到m阶),需要N = O(ϵ−2m)数量的参数才能达到误差 ϵ,这相当于 α = m/2。我们的方法假设存在平滑的Kolmogorov-Arnold表示,将高维函数分解为多个一维函数,从而得到 α = k+1(其中k是样条的分段多项式阶数)。我们选择k = 3的三次样条,因此 α = 4,这是与其他工作相比最大和最好的缩放指数。我们将在第3.1节中展示,实际上KAN可以实现这个界限 α = 4,而先前的工作 [18] 报告说,MLP甚至在饱和较慢的界限(例如,α = 1)上也存在问题,并且很快就会出现平台。当然,我们可以增加k以匹配函数的平滑性,但是如果k过高可能会导致过于振荡,从而导致优化问题。
KAT和UAT之间的比较。全连接神经网络的强大性质由于普适逼近定理(UAT)而得到证明,该定理表明,给定一个函数和误差容限ϵ > 0,具有 k > N(ϵ)个神经元的两层网络可以在误差ϵ内近似函数。然而,UAT不保证N(ϵ)如何随ϵ扩展。实际上,它受到维度诅咒的影响,在某些情况下,N已经被证明与d呈指数增长。KAT和UAT之间的差异是KAN利用了函数的固有低维表示,而MLP没有。事实上,我们将展示KAN与符号函数很好地对齐,而MLP则没有。
2.4 准确性:网格扩展
原则上,样条可以被调整得足够精确以逼近目标函数,因为网格可以被调整得任意细。这一优点被KAN所继承。相比之下,MLP没有“细化”的概念。诚然,增加MLP的宽度和深度可能会提高性能(“神经缩放定律”)。然而,这些神经缩放定律很慢(在上一节中讨论)。而且,由于需要独立训练不同大小的模型,它们的获取成本也很高。相比之下,对于KAN,可以先训练一个参数较少的KAN,然后通过简单地使其样条网格更细,而无需从头重新训练较大的模型,将其扩展为参数更多的KAN。
接下来我们描述如何执行网格扩展(如图2.2右所示),基本上是将一个新的细网格拟合到一个旧的粗网格样条上。假设我们要在有界区间[a, b]上用k阶B样条逼近一个一维函数f。一个粗网格,有G1个间隔,在 处有网格点,它被扩展到 。有G1 + k个B样条基函数,第i个B样条Bi(x)只在 上非零 。然后在粗网格上,f可表示为这些B样条基函数的线性组合 。给定一个包含G2个间隔的更细网格,精细网格上的f相应地为 。参数c′j可以通过将 之间的距离(在某些x的分布上)最小化来从参数 初始化:

我们可以通过最小二乘算法实现这一点。我们针对KAN中的所有样条独立进行网格扩展。
玩具示例:类似楼梯状的损失曲线。我们使用一个玩具示例 来展示网格扩展的效果。在图2.3(左上角),我们展示了[2, 5, 1] KAN的训练和测试RMSE。网格点的数量从3开始,每200个LBFGS步增加到更高的值,最终达到1000个网格点。很明显,每次进行细粒度化时,训练损失都比以前下降得更快(除了具有1000个点的最细网格,由于糟糕的损失地形,优化可能停止工作)。然而,测试损失首先下降,然后上升,显示出一个U形,这是由于偏差-方差的权衡(欠拟合与过拟合)。我们推测,当参数数量与数据点数量匹配时,最佳的测试损失是在插值阈值处达到的。由于我们的训练样本有1000个,而[2, 5, 1] KAN的总参数为15G(其中G是网格间隔的数量),我们预期插值阈值为 ( G = 1000/15 approx 67 ),这大致符合我们实验观察到的值 ( G approx 50 ) 。
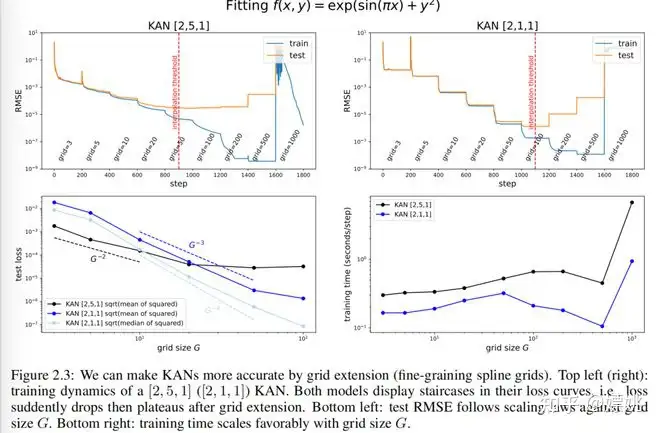
小型KAN具有更好的泛化能力。这是我们能够实现的最佳测试性能吗?请注意,合成任务可以完全由[2, 1, 1] KAN表示,因此我们训练了一个[2, 1, 1] KAN并在图2.3右上角呈现了训练动态。有趣的是,它甚至可以比[2, 5, 1] KAN实现更低的测试损失,具有更清晰的楼梯结构,并且由于参数更少,插值阈值被延迟到较大的网格大小。这凸显了选择KAN架构的微妙之处。如果我们不知道问题结构,如何确定最小的KAN形状?在第2.5节中,我们将提出一种通过正则化和剪枝自动发现这种最小的KAN架构的方法。
Scaling laws:尺度规律:与理论比较。我们还对测试损失随网格参数数量增加而减少的情况感兴趣。在图2.3(左下角),[2,1,1] KAN的测试RMSE大致按照 的比例尺进行缩放。然而,根据定理2.1,我们预期测试RMSE按照 的尺度进行缩放。
我们发现,样本间的错误不是均匀的。这可能归因于边界效应。事实上,有一些样本的误差显著大于其他样本,导致整体缩放变慢。如果我们绘制平方损失的中位数(而不是均值)的平方根,我们会得到接近 的尺度。尽管存在这种亚最优性(可能是由于优化造成的),但KAN仍然比MLP具有更好的尺度规律,用于数据拟合(图3.1)和PDE求解(图3.3)。此外,训练时间随网格点数量G的变化也是有利的,如图2.3右下所示。
外部与内部自由度。KANs突出显示的一个新概念是外部与内部自由度(参数)的区别。节点如何连接的计算图表示外部自由度(“dofs”),而激活函数内部的网格点表示内部自由度。KANs受益于它们既具有外部dofs也具有内部dofs。外部dofs(MLPs也具有但样条不具有)负责学习多个变量的组合结构。内部dofs(样条也具有但MLPs不具有)负责学习单变量函数。
2.5 为了可解释性:简化 KAN 并使其具有交互性
对于可解释性:简化KANs并使其互动化。上一小节的一个问题是我们不知道如何选择最能匹配数据集结构的KAN形状。例如,如果我们知道数据集是通过符号公式 生成的,那么我们知道[2, 1, 1] KAN能够表示这个函数。然而,在实践中,我们事先不知道这些信息,因此能够自动确定这种形状将是很好的。这个想法是从足够大的KAN开始,通过稀疏正则化和剪枝进行训练。我们将展示这些被剪枝的KANs比未剪枝的KANs更加可解释。为了使KANs最大程度上具有可解释性,我们在第2.5.1节提出了一些简化技术,并在第2.5.2节中提供了用户如何与KANs进行互动以增强可解释性的示例。
2.5.1 简化技术
1. 稀疏化。 对于MLPs,使用L1正则化线性权重来倾向于稀疏性。KANs可以采用这个高层次的想法,但需要两个修改:
(1) 在KANs中没有线性的“权重”。线性权重被可学习的激活函数替代,因此我们应该定义这些激活函数的L1范数。
(2) 我们发现L1对于KANs的稀疏化不足够;相反,额外的熵正则化是必要的(更多细节请参见附录C)。
我们定义激活函数ϕ的L1范数为其在其Np个输入上的平均幅值,即
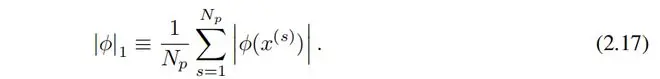
那么对于一个具有 个输入和 个输出的KAN层Φ,我们定义Φ的L1范数为所有激活函数的L1范数之和,即

2. 可视化。 当我们可视化一个KAN时,为了对大小有所感知,我们将激活函数 的透明度设置为与 成比例,其中β = 3。因此,幅度较小的函数会变得模糊,以便我们专注于重要的部分。

4. 符号化。 在某些情况下,我们怀疑某些激活函数实际上是符号化的(例如,cos或log),我们提供了一个接口来将它们设置为指定的符号形式,fix_symbolic(l,i,j,f) 可以将(l,i,j)激活设置为f。然而,我们不能简单地将激活函数设置为精确的符号公式,因为其输入和输出可能具有偏移和缩放。因此,我们从样本中获取预激活x和后激活y,并拟合仿射参数(a,b,c,d),使得y ≈ cf(ax + b) + d。拟合是通过迭代网格搜索a、b和线性回归来完成的。
除了这些技术外,我们还提供了其他工具,允许用户对KANs进行更精细的控制,详见附录A。
2.5.2 一个玩具示例:人类如何与 KAN 交互
以上我们提出了一些用于简化KANs的技术。我们可以将这些简化选择视为可以点击的按钮。与这些按钮进行交互的用户可以决定点击哪个按钮最有希望,以使KANs更具解释性。我们在下面用一个例子展示了用户如何与KAN进行交互,以获得最大程度的可解释结果。
让我们再次考虑回归任务。
给定数据点 ,一个假设的用户 Alice 对找出符号公式感兴趣。Alice 与 KANs 的交互步骤如下所述(如图2.4所示):
第一步:使用稀疏化进行训练。 从一个全连接的 [2, 5, 1] KAN 开始,通过稀疏化正则化进行训练,可以使其变得非常稀疏。隐藏层中的 5 个神经元中的 4 个似乎是无用的,因此我们想要将它们剪枝掉。
第二步:剪枝。 自动剪枝看起来会丢弃除最后一个之外的所有隐藏神经元,留下一个 [2, 1, 1] KAN。激活函数似乎是已知的符号函数。
第三步:设置符号函数。 假设用户可以正确地从观察 KAN 图中猜出这些符号公式,他们可以设置

如果用户没有领域知识或不知道这些激活函数可能是哪些符号函数,我们提供一个 suggest_symbolic 函数来建议符号候选项。
第四步:进一步训练。 在对网络中的所有激活函数进行符号化之后,唯一剩下的参数是仿射参数。我们继续训练这些仿射参数,当我们看到损失降到机器精度时,我们知道我们已经找到了正确的符号表达式。
第五步:输出符号公式。使用 Sympy 计算输出节点的符号公式。用户获得了 ,这是真实的答案(我们只显示了 π 的两位小数)。
备注:为什么不使用符号回归(SR)?对于这个例子使用符号回归是合理的。然而,符号回归方法通常是脆弱的且难以调试的。它们最终要么返回成功要么返回失败,而不会输出可解释的中间结果。相比之下,KANs在函数空间中进行连续搜索(使用梯度下降),因此它们的结果更连续,因此更稳健。此外,由于KANs的透明性,用户对KANs具有更多的控制权,相比之下,符号回归则没有这么多。我们将在第4.4节中展示这方面的例子。更一般地说,当目标函数不是符号化时,符号回归将失败,但KANs仍然可以提供有意义的结果。例如,除非提前提供,否则符号回归无法学习特殊函数(例如贝塞尔函数),但KANs可以使用样条在数值上进行近似(参见图4.1(d))。
3. KAN 准确性
在本节中,我们展示了KANs在各种任务(回归和PDE求解)中比MLPs更有效地表示函数。在比较两个模型族时,公平的做法是同时比较它们的准确性(损失)和复杂性(参数数量)。我们将展示KANs显示出比MLPs更有利的帕累托前沿。此外,在第3.5节中,我们还将展示KANs可以在连续学习中自然地工作,而不会发生灾难性遗忘。
3.1 数据集
在第 2.3 节中,我们的理论建议使用模型参数 N 来测试 RMSE 损失 ℓ 缩放为 。然而,这依赖于柯尔莫哥洛夫-阿诺德表示的存在。作为健全性检查,我们构建了五个我们知道具有平滑 KA 表示的示例:

我们通过每200步增加一次网格点的方式来训练这些 KAN,总共覆盖了 G = {3, 5, 10, 20, 50, 100, 200, 500, 1000}。我们以不同深度和宽度的 MLP 作为基线进行训练。MLP 和 KAN 都使用 LBFGS 进行了总共 1800 步的训练。我们在图 3.1 中将测试的 RMSE 作为参数数量的函数进行绘制,结果显示 KAN 比 MLP 有更好的缩放曲线,特别是对于高维示例。为了比较,我们绘制了从我们的 KAN 理论预测的红色虚线(α = k + 1 = 4),以及从 Sharma & Kaplan [17] 预测的黑色虚线(α = (k+ 1)/d = 4/d)。KAN 几乎可以达到陡峭的红色线条,而 MLP 却难以以与较慢的黑色线条相同的速度收敛,并且很快就进入了平稳状态。我们还注意到,对于最后一个例子,2 层 KAN [4, 9, 1] 的行为要比 3 层 KAN(形状 [4, 2, 2, 1])差得多。这突显了更深的 KAN 具有更强的表达能力,与 MLP 相同:深层 MLP 比浅层 MLP 有更强的表达能力。
3.2 特殊功能
以上结果的一个重要限制是,我们假设了对“真实”KAN形状的了解。在实践中,我们并不知道KA表示的存在。即使我们被承诺存在这样的KA表示,我们也无法事先知道KAN的形状。多变量特殊函数是这样的情况,因为如果多变量特殊函数(例如,贝塞尔函数 f(ν, x) = Jν(x))可以被写成只涉及单变量函数和求和的KA表示,那么这在数学上是令人惊讶的。我们下面将展示:
(1) 发现(近似的)紧致的KA表示是可能的,从Kolmogorov-Arnold表示的角度揭示特殊函数的新的数学特性。
(2) KANs 在表示特殊函数方面比 MLPs 更高效和准确。
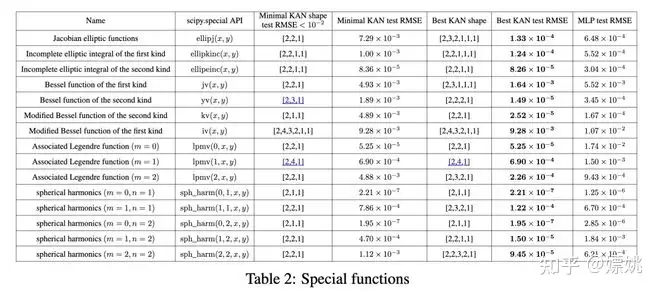
我们收集了15个在数学和物理中常见的特殊函数,总结如表2所示。我们选择了固定宽度为5或100的MLPs,并在{2, 3, 4, 5, 6}中进行深度扫描。我们同时运行了有和无修剪的KANs。无修剪的KANs:我们固定KAN的形状,其宽度设置为5,深度在{2, 3, 4, 5, 6}中扫描。有修剪的KANs:我们使用第2.5.1节中的稀疏化 和修剪技术,从一个固定形状的KAN中获得一个较小的修剪KAN。每个KAN都初始化为具有G = 3,使用LBFGS进行训练,每200步增加一次网格点以覆盖G = {3, 5, 10, 20, 50, 100, 200}。对于每个超参数组合,我们运行3个随机种子。
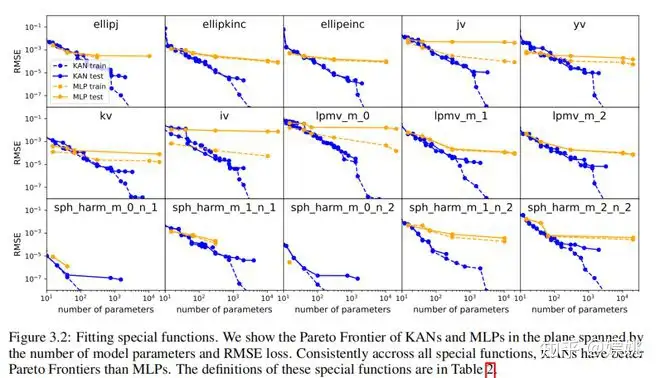
对于每个数据集和每个模型族(KANs或MLPs),我们在(参数数量,RMSE)平面上绘制Pareto前沿,如图3.2所示。KANs的性能一直显示出比MLPs更好,即KANs可以在给定相同数量的参数时实现更低的训练/测试损失。此外,我们在表2中报告了我们自动发现的特殊函数的(令人惊讶地紧凑的)KANs的形状。从一方面来说,解释这些紧凑表示在数学上意味着什么是很有趣的(我们在附录F中的图F.1和F.2中包含了KAN的插图)。另一方面,这些紧凑的表示意味着将一个高维查找表分解成几个1D查找表的可能性,这可能会节省大量内存,并且在推理时执行少量的加法带来的开销几乎可以忽略不计。
3.3 费曼数据集
在第3.1节中的设置是当我们清楚地知道“真实”的KAN形状时。在第3.2节中的设置是当我们完全不知道“真实”的KAN形状时。本部分研究了一个处于中间状态的设置:在给定数据集结构的情况下,我们可以手动构建KANs,但我们不确定它们是否是最优的。在这种情况下,比较人工构建的KANs和通过修剪(第2.5.1节中的技术)自动发现的KANs是很有趣的。
费曼数据集。费曼数据集收集了许多来自费曼教科书[20, 21]的物理方程。对于我们的目的,我们对至少包含2个变量的Feynman_no_units数据集中的问题感兴趣,因为对于KANs来说,单变量问题是微不足道的(它们简化为1D样条曲线)。来自费曼数据集的一个样本方程是相对论速度相加公式
该数据集可以通过随机抽取 ,并计算 构建而成。给定许多元组 训练一个神经网络旨在从 u 和 v 预测 f。我们感兴趣的是 (1) 神经网络在测试样本上的表现如何;(2) 我们能从神经网络中学到多少关于问题结构的信息。
我们比较了四种类型的神经网络:
(1) 人工构建的 KAN。给定一个符号公式,我们将其重写为 Kolmogorov-Arnold 表示。例如,要将两个数字 x 和 y 相乘,我们可以使用等式 ,对应于一个 [2, 2, 1] 的 KAN。构建的形状列在表3的“人工构建的 KAN 形状”中。
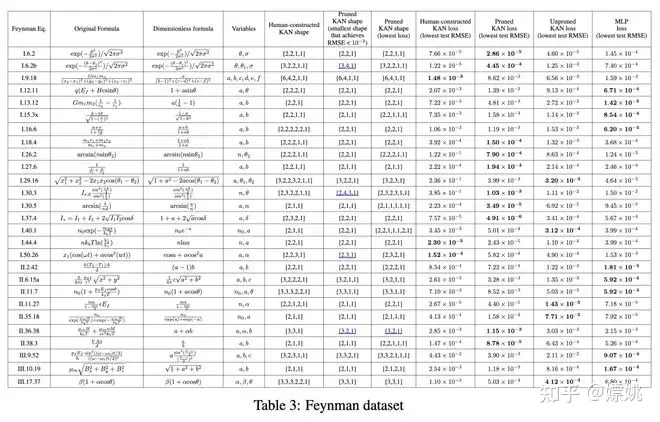
(2) 无修剪的 KAN。我们将 KAN 形状固定为宽度 5,深度在 {2,3,4,5,6} 中扫描。
(3) 有修剪的 KAN。我们使用第2.5.1节中的稀疏化 和修剪技术,从(2)中的固定形状的 KAN 中获得一个较小的 KAN。
(4) MLPs,固定宽度为20,深度在 {2, 3, 4, 5, 6} 中扫描,并从 {Tanh, ReLU, SiLU} 中选择激活函数。
每个 KAN 初始化为 G = 3,使用 LBFGS 进行训练,每200步增加一次网格点以覆盖 G = {3, 5, 10, 20, 50, 100, 200}。对于每个超参数组合,我们尝试3个随机种子。对于每个数据集(方程)和每种方法,我们报告了在随机种子和深度中最佳模型的结果(最小的 KAN 形状或最低的测试损失)在表3中。我们发现 MLPs 和 KANs 的表现平均相当。对于每个数据集和每个模型族(KANs 或 MLPs),我们在由参数数量和 RMSE 损失构成的平面上绘制 Pareto 前沿,如附录 D 中的图D.1所示。我们推测费曼数据集对于 KANs 来说过于简单,无法进一步改善,因为变量依赖通常是平滑或单调的,这与特殊函数的复杂性形成对比,后者通常表现出振荡行为。
自动发现的 KANs 比人工构建的更小。我们在表3的两列中报告了修剪后的 KAN 形状;一列是能够达到合理损失(即测试 RMSE 小于 10^−2)的最小修剪 KAN 形状;另一列是达到最低测试损失的修剪 KAN。为了完整起见,我们在附录 D(图 D.2 和 D.3)中可视化了所有的 54 个修剪 KANs。观察到自动发现的 KAN 形状(无论是最小的还是最佳的)通常比我们的人工构建更小是很有趣的。这意味着 KA 表示可能比我们想象的更有效。与此同时,这可能会使解释变得微妙,因为信息被压缩到比我们习惯的空间更小的空间中。
以相对论速度合成 为例。我们的构造相当深,因为我们假设 u、v 的乘积将使用两层(见图4.1(a)),1 + uv 的倒数将使用一层,以及 的乘积将使用另外两层,总共5层。然而,自动发现的 KANs 只有 2 层深!事后看来,如果我们回想起相对论中的快度技巧:定义两个“快度” 速度的相对论合成在快度空间中是简单的加法,即 ,这可以通过一个两层的 KAN 实现。假设我们不知道物理中的快度概念,我们可能可以直接从 KANs 中发现这个概念,而无需进行试错的符号操作。KANs 的可解释性可以促进科学发现,这是第 4 节的主题。
3.4 求解偏微分方程
我们考虑具有零狄利克雷边界数据的泊松方程。 ,考虑 PDE
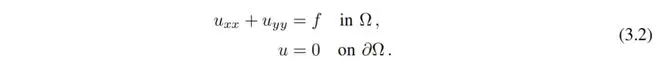
我们考虑的数据是 ,其中 是真实解。我们使用物理信息神经网络(PINNs)[22, 23]的框架来解决这个偏微分方程,损失函数为
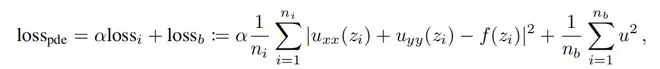
在这里,我们使用 lossi 表示内部损失,通过对域内的 ni 个点 进行均匀采样离散化并评估得到,类似地,我们使用 lossb 表示边界损失,通过对边界上的 nb 个点进行均匀采样离散化并评估得到。α 是平衡这两项影响的超参数。
我们将 KAN 架构与使用相同超参数 ni = 10000、nb = 800 和 α = 0.01 的 MLPs 进行比较。我们测量 范数和能量 的误差,并观察到 KAN 达到了更好的缩放规律,误差更小,使用了更小的网络和更少的参数;见图3.3。因此,我们推测 KANs 可能有潜力作为偏微分方程模型减缩的良好神经网络表示。
3.5 持续学习
当前机器学习中的灾难性遗忘是一个严重的问题。当人类掌握了一个任务并转向另一个任务时,他们不会忘记如何执行第一个任务。不幸的是,神经网络并不是这样。当神经网络在任务1上训练后转移到任务2上训练时,网络很快就会忘记如何执行任务1。人工神经网络与人脑的一个关键区别在于,人脑在空间中具有功能上不同的模块。当学习新任务时,结构重新组织仅发生在负责相关技能的局部区域,而其他区域保持不变。大多数人工神经网络,包括MLPs,没有这种局部性概念,这可能是灾难性遗忘的原因。
我们展示了KANs具有局部可塑性,并且可以通过利用样条的局部性来避免灾难性遗忘。这个想法很简单:由于样条基是局部的,一个样本只会影响附近的几个样条系数,而远处的系数保持不变(这是期望的,因为远处的区域可能已经存储了我们想要保留的信息)。相比之下,由于MLPs通常使用全局激活函数,例如ReLU/Tanh/SiLU等,任何局部变化都可能无法控制地传播到远处的区域,破坏那里存储的信息。
我们使用一个玩具示例来验证这种直觉。1D回归任务由5个高斯峰组成。每个峰附近的数据被依次呈现给KANs和MLPs,如图3.4的顶部行所示。每个训练阶段后的KAN和MLP预测结果分别显示在中间和底部行。正如预期的那样,KAN仅重塑当前阶段存在数据的区域,而将以前的区域保持不变。相比之下,MLPs在看到新数据样本后重新建模整个区域,导致灾难性遗忘。
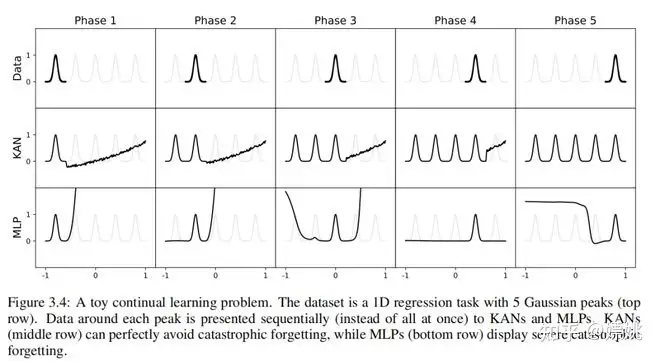
在这里,我们只是简单地呈现了我们在一个极其简单的例子上的初步结果,以展示如何可能利用KANs中的局部性(借助样条参数化)来减少灾难性遗忘。然而,我们还不清楚我们的方法是否可以推广到更现实的设置,这留待将来的工作。我们还希望研究我们的方法如何与持续学习中的SOTA方法相连接和结合。
4 个 KAN 是可解释的
在本节中,我们展示了KANs(可解释性自适应网络)在我们在第2.5节中开发的技术的支持下具有可解释性和交互性。我们希望测试KANs的使用不仅限于合成任务(第4.1和4.2节),还包括在真实科学研究中的应用。我们证明了KANs可以(重新)发现结构理论中的高度非平凡关系(第4.3节)和凝聚态物理学中的相变边界(第4.4节)。由于它们的准确性(最后一节)和可解释性(本节),KANs可能成为AI + 科学的基础模型。
4.1 监督演示数据集
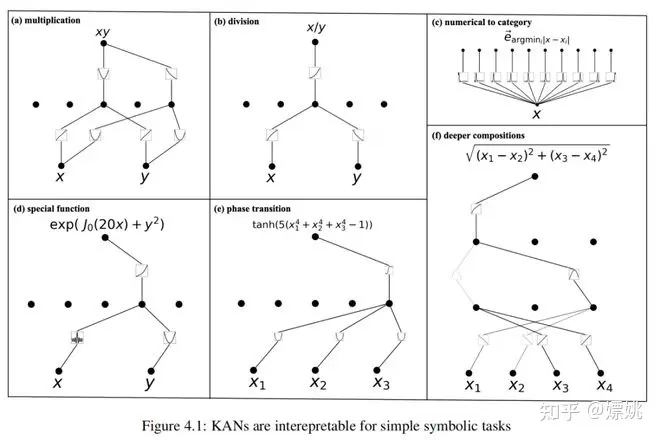
我们首先检验KANs揭示符号公式中的组合结构的能力。下面列出了六个示例,并在图4.1中可视化它们的KANs。KANs能够揭示这些公式中存在的组合结构,并学习正确的单变量函数。
(a)乘法f(x,y)= xy。一个[2,5,1] KAN被修剪成一个[2,2,1] KAN。学习的激活函数是线性和二次的。从计算图中,我们可以看到它计算xy的方式是利用了2xy = (x + y)² - (x² + y²)。
(b)正数的除法f(x,y)= x/y。一个[2,5,1] KAN被修剪成一个[2,1,1] KAN。学习的激活函数是对数和指数函数,而KAN通过利用恒等式x/y = exp(logx - logy)来计算x/y。
(c)数值到分类的转换。任务是将[0,1]中的实数转换为它的第一个小数位数(作为one hot编码),例如,0.0618 → [1, 0, 0, 0, 0, · · · ],0.314 → [0, 0, 0, 1, 0, · · · ]。注意,学习到的激活函数是位于相应小数位周围的尖峰。
(d) 特殊函数f(x, y) = exp(J0(20x) + y²)。符号回归的一个限制是,如果未提供特殊函数作为先验知识,它将永远无法找到特殊函数的正确公式。KANs可以学习特殊函数 - 高度波动的贝塞尔函数J0(20x)是通过KAN(数值上)学习到的。
(e) 相变f(x1, x2, x3) = tanh(5(x⁴₁ + x⁴₂ + x⁴₃ - 1))。相变在物理学中非常重要,因此我们希望KANs能够检测相变并识别正确的序参量。我们使用tanh函数来模拟相变行为,序参量是x₁、x₂、x₃的四次项的组合。在KAN训练之后,四次依赖性和tanh依赖性都会出现。这是在第4.4节讨论的局部化相变的简化情况。
(f) 更深的组合f(x₁, x₂, x₃, x₄) = p(x₁ - x₂)² + (x₃ - x₄)²。要计算这个函数,我们需要恒等函数、平方函数和平方根,这至少需要一个三层的KAN。事实上,我们发现一个[4, 3, 3, 1] KAN可以自动修剪成一个[4, 2, 1, 1] KAN,这恰好对应于我们预期的计算图。
在附录D和F的图D.2、D.3、F.1、F.2中可视化了来自Feynman数据集和特殊函数数据集的更多示例。
4.2 无监督演示数据集
通常,科学发现被阐述为监督学习问题,即给定输入变量x₁、x₂、...、xd和输出变量y,我们希望找到一个可解释的函数f,使得y ≈ f(x₁、x₂、...、xd)。然而,另一种类型的科学发现可以被阐述为无监督学习,即给定一组变量(x₁、x₂、...、xd),我们希望发现变量之间的结构关系。具体来说,我们想找到一个非零的f,使得

如果能够设计出一种解决无监督问题的算法,它将比监督问题具有相当大的优势,因为它仅需要特征集S = (x₁、x₂、...、xd)。另一方面,监督问题试图预测特征的子集,即它将 t划分为要学习的函数的输入和输出特征。如果没有领域专业知识来指导拆分,那么有2^d - 2种可能性,使得 。通过使用无监督方法,可以避免这种指数级的大规模监督问题空间。这种无监督学习方法将对第4.3节中的结构数据集具有价值。谷歌Deepmind团队[29]手动选择了签名作为目标变量,否则他们将面临上述的组合问题。这引发了一个问题,即我们是否可以直接解决无监督学习。我们在下面介绍我们的方法和一个玩具例子。
我们通过将无监督学习问题转化为对所有d个特征进行监督学习,而不需要选择划分来解决无监督学习问题。基本思想是学习一个函数f(x₁, . . . , xd) = 0,使得f不是0函数。为此,类似于对比学习,我们定义了正样本和负样本:正样本是真实数据的特征向量。负样本是通过特征损坏构造的。为了确保每个拓扑不变量的整体特征分布保持不变,我们通过对整个训练集的每个特征进行随机排列来进行特征损坏。现在我们想要训练一个网络g,使得 ,从而将问题转化为一个监督问题。然而,请记住我们最初希望 。我们可以通过令g = σ ◦ f来实现这一点,其中 是一个具有小宽度w的高斯函数,它可以方便地通过形状为[...]的KAN实现,其最后一个激活函数设置为高斯函数σ,而所有前面的层形成f。除了上述修改之外,其他所有内容在监督训练中都是相同的。
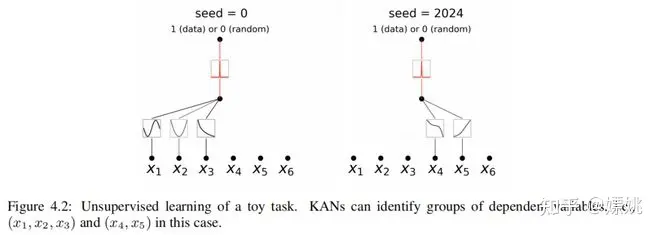
现在我们演示无监督范例在一个合成例子中的工作原理。让我们考虑一个6维数据集,其中(x₁、x₂、x₃)是依赖变量,使得 是依赖变量,其中 与其他变量无关。在图4.2中,我们展示了对于seed = 0,KAN揭示了x₁、x₂和x₃之间的函数依赖关系;对于另一个seed = 2024,KAN揭示了x₄和x₅之间的函数依赖关系。我们的初步结果依赖于随机性(不同的种子)来发现不同的关系;在未来,我们希望研究一种更系统和更可控的方式来发现完整的关系集。即便如此,我们的工具在当前状态下也可以为科学任务提供洞察力。我们在第4.3节中呈现了我们在结构数据集上的结果。
4.3 数学应用:纽结理论
结构理论是低维拓扑学的一个领域,它揭示了三维流形和四维流形的拓扑方面,并具有多种应用,包括生物学和拓扑量子计算。数学上,一个结构K是S¹嵌入到S³中。如果一个结构K和K'可以通过环境空间S³的变形相互转化,则它们是拓扑等价的,此时我们写作[K] = [K']。一些结构是拓扑平凡的,意味着它们可以平滑变形为标准圆。结构具有各种变形不变特征f,称为拓扑不变量,可以用来表明两个结构在拓扑上不等价,即如果f(K) = f(K'),则[K] = [K']。在某些情况下,拓扑不变量具有几何性质。例如,一个双曲结构K具有一个结构补S³ \ K,它具有一个称为双曲体积的拓扑不变量的标准双曲度量g,其中volg(K)是一个拓扑不变量。其他拓扑不变量具有代数性质,如Jones多项式。
鉴于结构在数学中的基础性质和其应用的重要性,研究机器学习是否能够产生新的结果是有趣的。例如,在[30]中,强化学习被用于建立某些结构的带状性,这排除了许多对光滑的四维庞加莱猜想的潜在反例。
Supervised learning 在[29]中,利用监督学习和人类领域专家得出了一个关于代数和几何结构不变量的新定理。在这种情况下,梯度显著性识别了监督问题的关键不变量,这导致领域专家提出了一个猜想,随后得到了进一步的改进和证明。我们研究KAN是否能够在相同问题上取得良好的可解释结果,即预测结构的签名。他们从研究结构理论数据集中得到的主要结果是:
(1)他们使用网络归因方法发现,签名σ主要依赖于子午线距离µ(实部µr,虚部µi)和经度距离λ。
(2)后来人类科学家发现σ与斜率有很高的相关性≡ Re(λ/µ) = λµr / (µ²r+µ²i),并推导出了|2σ - 斜率|的界限。
我们将在下文中展示,KAN不仅可以利用更小的网络和更多的自动化重新发现这些结果,还可以呈现一些有趣的新结果和见解。
为了研究(1),我们将17个结构不变量视为输入,将签名视为输出。与[29]中的设置类似,签名(偶数)被编码为one-hot向量,并使用交叉熵损失训练网络。我们发现一个极小的[17, 1, 14] KAN能够达到81.6%的测试准确率(而Deepmind的4层宽度为300的MLP达到78%的测试准确率)。[17, 1, 14] KAN(G = 3,k = 3)有约200个参数,而MLP有约3 × 10^5个参数,如表4所示。值得注意的是,KAN在准确性和参数效率上都可以比MLP更好。就可解释性而言,我们根据每个激活的大小调整透明度,因此可以立即清楚地看出哪些输入变量是重要的,无需进行特征归因(见图4.3左图):签名主要依赖于µr,略微依赖于µi和λ,而对其他变量的依赖性较小。然后,我们对三个重要变量训练了一个[3, 1, 14] KAN,得到测试准确率78.2%。我们的结果与[29]中的结果有一个细微的差别:他们发现签名主要依赖于µi,而我们发现签名主要依赖于µr。这种差异可能是由于细微的算法选择导致的,但是这促使我们进行了以下实验:(a)消融研究。我们发现µr对准确性的贡献大于µi(见图4.3):例如,单独µr可以达到65.0%的准确率,而单独µi只能达到43.8%的准确率。(b)我们找到了一个符号公式(见表5),它只涉及µr和λ,但可以达到77.8%的测试准确率。

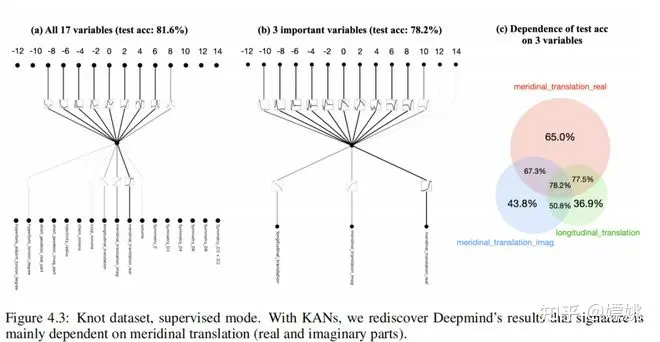
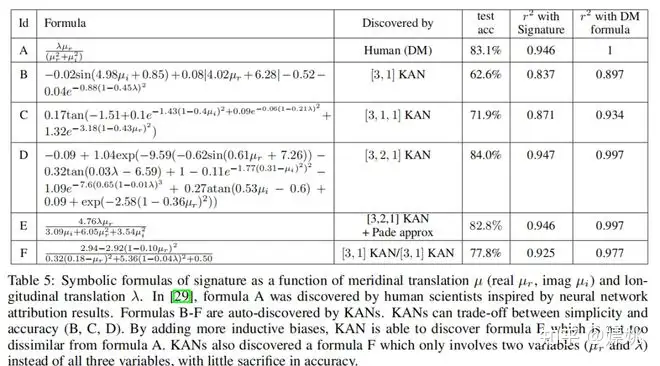
表5:签名的符号公式作为子午线平移µ(实部µr,虚部µi)和经度平移λ的函数。在[29]中,公式A是由受神经网络归因结果启发的人类科学家发现的。公式B-F是由KAN自动发现的。KAN可以在简单性和准确性之间进行权衡(B、C、D)。通过添加更多的归纳偏好,KAN能够发现与公式A并不完全不同的公式E。KAN还发现了一个只涉及两个变量(µr和λ)而不是所有三个变量的公式F,准确性损失很小。
为了研究(2),即获得σ的符号形式,我们将问题制定为回归任务。使用2.5.1节介绍的自动符号回归,我们可以将训练好的KAN转换成符号公式。我们训练了形状为[3, 1]、[3, 1, 1]、[3, 2, 1]的KAN,它们对应的符号公式显示在表5 B-D中。很明显,通过拥有更大的KAN,准确性和复杂性都会增加。因此,KAN不仅提供了单一的符号公式,而且提供了一整个帕累托前沿的公式,权衡了简单性和准确性。然而,KAN需要额外的归纳偏好来进一步简化这些方程,以重新发现[29]中的公式(表5 A)。我们进行了两种场景的测试:(1)在第一种情况下,我们假设地面真实公式具有多变量帕德表示(两个多变量泰勒级数的除法)。我们首先训练[3, 2, 1],然后将其拟合为帕德表示。我们可以在表5中获得公式E,该公式与Deepmind的公式相似。(2)我们假设除法对于KAN来说并不是很可解释,因此我们训练了两个KAN(一个用于分子,另一个用于分母),然后手动进行除法。令人惊讶的是,我们最终得到了公式F(在表5中),它只涉及µr和λ,虽然µi也被提供但被KAN忽略了。
到目前为止,我们已经重新发现了[29]中的主要结果。令人惊讶的是,KAN使这一发现变得非常直观和方便。与使用特征归因方法相比(这是一种很好的方法),人们可以简单地盯着KAN的可视化结果。此外,自动符号回归还使得符号公式的发现变得更加容易。
在接下来的部分,我们提出了一种新的“AI for Math”范式,这种范式不包含在Deepmind的论文中,我们旨在使用KAN的无监督学习模式发现结构不变量中的更多关系(除了签名)。
无监督学习正如我们在第4.2节中提到的,无监督学习是一种更有前景的设置,因为它避免了输入和输出变量的手动分区,这些变量可能有着组合多种可能性。在无监督学习模式下,我们将所有的18个变量(包括签名)都视为输入,使它们处于同等地位。结节点数据是正样本,我们随机打乱特征以获取负样本。一个[18, 1, 1] KAN 被训练来分类给定的特征向量是否属于正样本(1)或负样本(0)。我们手动设置第二层的激活函数为高斯函数,峰值位于零点,因此正样本将在(附近)零点处激活,隐含地给出了结节点不变量 的关系,其中xi表示一个特征(不变量),gi是相应的激活函数,可以从 KAN 图表中轻松读取。我们使用 来训练 KAN,以偏爱稀疏的输入组合,并使用seed = {0, 1, · · · , 99}。所有200个网络可以分为三个集群,具有代表性的 KAN 在图4.4中显示。这三组依赖变量为:
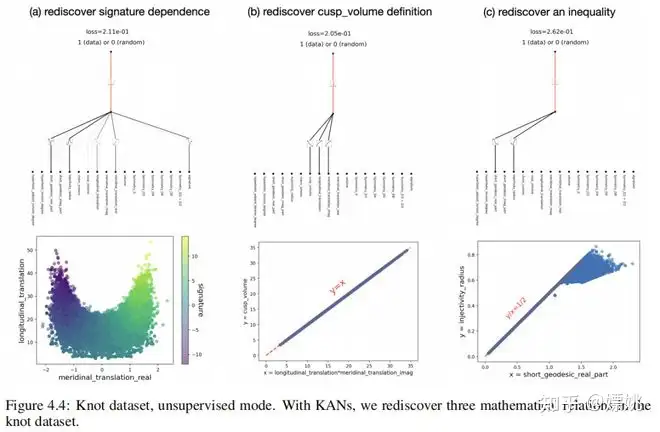
(1) 第一组依赖变量是签名、经度距离的实部和纬度距离,以及其他两个可以移除的变量(因为第三组)。这是上述签名依赖性的研究,所以很有趣的是在无监督模式下再次发现了这种依赖关系。
(2) 第二组变量涉及尖峰体积 V、经度平移的实部µr 和纬度平移λ。它们的激活函数都像对数函数(可以通过第2.5.1节中暗示的符号功能进行验证)。因此,关系为−log V + log µr + log λ = 0,这等效于 V = µrλ,根据定义是正确的。然而,令人欣慰的是我们在没有任何先验知识的情况下发现了这种关系。
(3) 第三组变量包括短测地线的实部 gr 和逐渐收缩的半径。它们的激活看起来在质上相同,但是由一个减号的差异,因此可以猜测这两个变量存在线性相关性。我们绘制了2D散点图,发现2倍的上界 gr,这也是一个众所周知的关系。
令人感兴趣的是,KAN 的无监督模式可以重新发现几个已知的数学关系。好消息是,KAN 发现的结果可能是可靠的;坏消息是,我们还没有发现任何新的东西。值得注意的是,我们选择了一个浅层的 KAN 进行简单的可视化,但更深层次的 KAN 可能会发现更多的关系(如果存在的话)。我们希望在未来的工作中研究如何通过更深的 KAN 发现更复杂的关系。
4.4 物理应用
Anderson局域化是一种基本现象,其中量子系统中的无序性导致电子波函数的局域化,使得所有传输被停止。在一维和二维情况下,尺度论证表明,对于微小的随机无序性,所有电子本征态都呈指数局域化。相比之下,在三维中,存在一个临界能量形成相界,将延展态与局域态分开,称为迁移边缘。对这些迁移边缘的理解对于解释固体中的金属-绝缘体转变等各种基本现象至关重要,以及在光子器件中的光局域效应。因此,开发能够显示迁移边缘的微观模型是必要的,以进行详细的研究。在低维中开发这样的模型通常更为实际,其中引入准周期性而不是随机无序性也可以导致将局域和延展相分开的迁移边缘。此外,解析迁移边缘的实验实现可以帮助解决对相互作用系统中局域化的争论。事实上,最近几项研究已经集中在识别这样的模型,并为它们的迁移边缘导出精确的解析表达式。
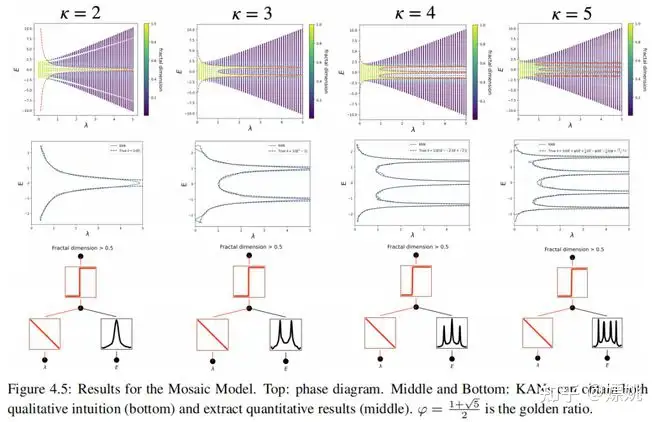
在这里,我们将KANs应用于从准周期紧束缚模型生成的数值数据,以提取它们的迁移边缘。特别地,我们研究了三类模型:马赛克模型(MM)、广义Aubry-André模型(GAAM)和修改后的Aubry-André模型(MAAM)。对于MM,我们验证了KAN准确提取迁移边缘作为能量的一维函数的能力。对于GAAM,我们发现从KAN得到的公式与真实情况非常接近。对于更复杂的MAAM,我们展示了这个框架的另一个符号可解释性的例子。用户可以通过“协作”的方式简化KANs获得的复杂表达式(以及相应的符号公式),其中人类生成假设以获得更好的匹配(例如,假设某些激活函数的形式),之后KANs可以进行快速的假设测试。
为了量化这些模型中状态的局域性,通常使用逆参与比(IPR)。第k个本征态的IPR,记作 ,定义为

这里的求和遍及站点指数。在这里,我们使用与局域性相关的测量 - 状态的分形维度,定义为
其中 N 是系统大小。Dk = 0(1) 表示局部(扩展)状态
Mosaic Model (MM) 马赛克模型(MM)我们首先考虑由 Hamiltonian [47] 定义的一类紧束缚模型
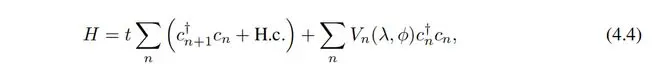
其中 t 是最近邻耦合, 是位置 n 处的湮灭(创建)算子,势能 Vn 由下式给出
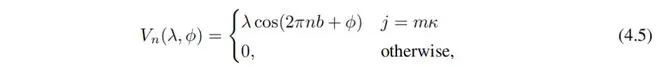
为了引入准周期性,我们将b设置为无理数(特别地,我们选择b为黄金比例 。κ是一个整数,准周期势以间隔κ发生。该模型的能量(E)谱通常包含由迁移边缘分隔的延展和局域区域。有趣的是,这里发现的一个独特特征是,迁移边缘存在于任意强的准周期势中(即系统中总是存在与局域状态共存的延展态)。
迁移边缘可以由 描述。g(λ, E) > 0和 0分别对应于局域和延展相。学习迁移边缘因此取决于学习“序参量”g(λ, E)。诚然,对于这类模型,这个问题可以通过许多其他理论方法来解决,但我们将在下面证明我们的KAN框架已经准备好并方便接受来自人类用户的假设和归纳偏差。
让我们假设一个名为Alice的假想用户,她是凝聚态物理学的新博士生,并且她被提供了一个[2, 1]的KAN作为辅助工具。首先,她意识到这是一个分类任务,因此明智地将第二层的激活函数设置为sigmoid,通过使用fix_symbolic功能。其次,她意识到学习整个二维函数g(λ, E)是不必要的,因为最终她只关心由g(λ, E) = 0确定的λ = λ(E)。因此,合理地假设g(λ, E) = λ − h(E) = 0。Alice通过再次使用fix_symbolic功能简单地将λ的激活函数设置为线性。现在Alice训练KAN网络,并方便地获得了迁移边缘,如图4.5所示。Alice可以获得直观的定性理解(底部)和数量化结果(中部),这些结果与基准真实值(顶部)非常匹配。
Generalized Andre-Aubry Model (GAAM) 广义安德烈-奥布里模型 (GAAM) 接下来我们考虑一类由哈密顿量定义的紧束缚模型 [46]

其中 t 是最近邻耦合, 是位置 n 处的湮灭(创建)算子,势能 Vn 由下式给出
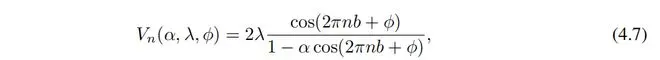
对于这些模型,迁移边缘由闭合形式表达式给出。这个表达式对于 α ∈ (−1, 1) 是光滑的。为了引入准周期性,我们再次将 b 设置为无理数(特别地,我们选择 b 为黄金比例)。
我们随机抽样模型参数:ϕ、α 和 λ(设置能量尺度 t = 1),并计算相应本征值以及对应本征态的分形维度,形成我们的训练数据集。这里要学习的“序参量”是 g(α, E, λ, ϕ) = αE + 2(λ − 1),而迁移边缘对应于 g = 0。让我们再次假设 Alice 想找出迁移边缘,但只能访问到 IPR 或分形维度数据,所以她决定使用 KAN 来帮助完成任务。Alice 希望模型尽可能小,因此她可以从一个大模型开始,使用自动修剪来得到一个小模型,或者她可以根据对给定问题复杂性的理解猜测一个合理的小模型。无论哪种方式,让我们假设她得到了一个 [4, 2, 1, 1] 的 KAN。首先,她将最后一个激活函数设置为 sigmoid,因为这是一个分类问题。她通过一些稀疏正则化训练她的 KAN,使准确率达到了 98.7%,并在图 4.6 (a) 的第一步中可视化训练好的 KAN。她观察到 ϕ 完全没有被注意到,这让她意识到迁移边缘与 ϕ 无关(与方程 (4.8) 一致)。此外,她观察到几乎所有其他激活函数都是线性或二次的,因此她打开了自动符号捕捉功能,将库限制为仅包含线性或二次函数。之后,她立即得到了一个已经是符号的网络(在图 4.6 (a) 的第二步中显示),准确率为 98.9%(甚至略高)。通过使用 symbolic_formula 功能,Alice 便可以方便地得到 g 的符号形式,如表 6 中 GAAM-KAN auto (第三行) 所示。也许她想删掉一些小项并将系数捕捉到小整数,这使她接近真实答案。
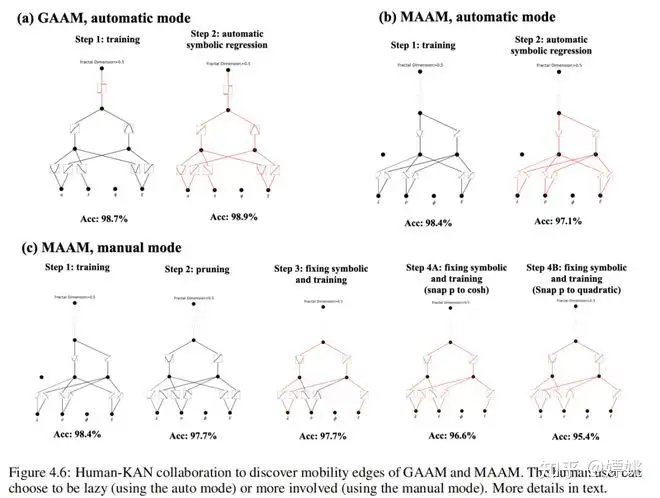
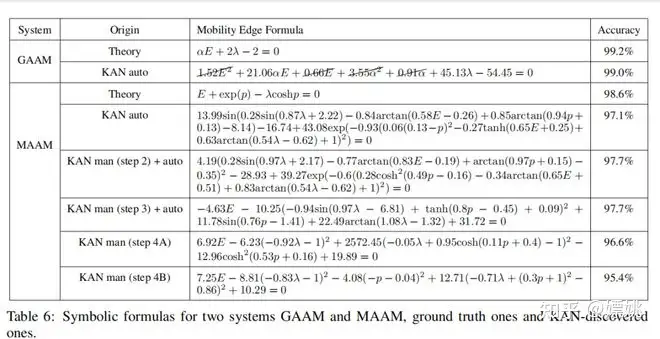
如果 Alice 使用符号回归方法,这个虚拟故事会完全不同。如果她幸运的话,符号回归可以返回准确的公式。然而,大多数情况下,符号回归不会返回有用的结果,而且 Alice 不可能“调试”或与符号回归的基础过程进行交互。此外,Alice 可能会感到不舒服/缺乏经验,在运行符号回归之前提供一组符号术语作为先验知识。相比之下,在 KAN 中,Alice 不需要提供任何先验信息。她可以先通过观察一个训练好的 KAN 得到一些线索,然后决定她想提出什么样的假设(例如,“所有激活函数都是线性或二次的”),并在 KAN 中实现她的假设。虽然 KAN 不太可能立即返回正确答案,但 KAN 总是会返回一些有用的东西,而且 Alice 可以与之合作以完善结果。
Modified Andre-Aubry Model (MAAM) 改进的 Andre-Aubry 模型 (MAAM) 我们考虑的最后一类模型是由哈密顿量定义的 [44]
其中 t 是空间中指数衰减耦合的强度,cₙ (cₙ†) 是在站点 n 的湮灭(产生)算符,而势能 Vₙ 给定为
与之前一样,为了引入准周期性,我们将 b 设置为无理数(黄金比例)。对于这些模型,迁移边缘由闭合形式表达式给出 [44]。
其中我们将 t1 eq(−p) 定义为最近邻跳跃强度,并在下面设置 t1 = 1。
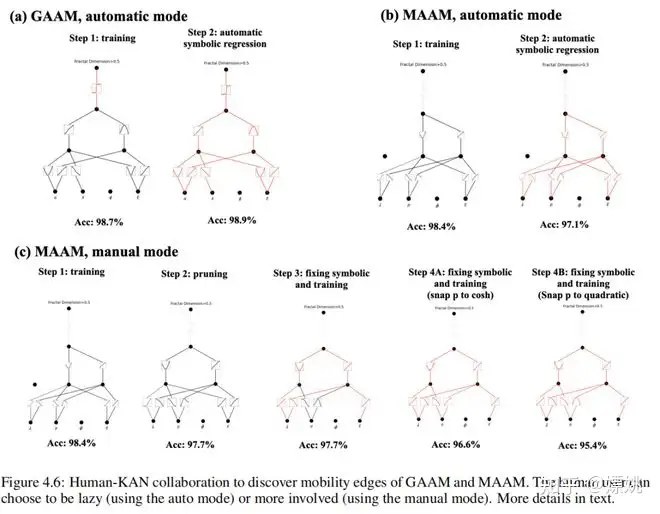
让我们假设 Alice 想要找出 MAAM 的迁移边缘。这个任务更加复杂,需要更多人类智慧。与上一个例子类似,Alice 从一个 [4, 2, 1, 1] 的 KAN 开始,并对其进行训练,但准确率只有约 75%,这是不可接受的。然后她选择了一个更大的 [4, 3, 1, 1] KAN,并成功地获得了 98.4% 的准确率,这是可以接受的(图 4.6 (b) 第一步)。Alice 注意到 KANs 并没有注意到 ϕ,这意味着迁移边缘与相位因子 ϕ 无关(与方程 (4.11) 一致)。如果 Alice 打开自动符号回归(使用包含 exp、tanh 等的大型库),她将获得在 Tabel 6-MAAM-KAN auto 中的一个复杂的公式,准确率为 97.1%。然而,如果 Alice 想要找到一个更简单的符号公式,她将希望使用手动模式,在其中自己进行符号捕捉。在这之前,她发现在训练后的 [4, 3, 1, 1] KAN 可以被修剪成 [4, 2, 1, 1],同时保持 97.7% 的准确率(图 4.6 (b))。Alice 可能认为除了依赖于 ρ 的激活函数外,其他激活函数都是线性或二次的,并通过使用 fix_symbolic 将它们手动捕捉为线性或二次函数。捕捉和重新训练后,更新后的 KAN 如图 4.6 (c) 第 3 步所示,保持了 97.7% 的准确率。从现在开始,Alice 可能基于她的先验知识做出两种不同的选择。在一种情况下,Alice 可能猜测 ρ 的依赖关系是双曲余弦函数,因此她将 ρ 的激活设置为双曲余弦函数。她重新训练 KAN 并获得 96.9% 的准确率(图 4.6 (c) 第 4A 步)。在另一种情况下,Alice 不知道双曲余弦函数对 ρ 的依赖关系,所以她追求简单性,并再次假设 ρ 的函数是二次的。她重新训练 KAN 并获得 95.4% 的准确率(图 4.6 (c) 第 4B 步)。如果她尝试了两种情况,她会意识到双曲余弦函数在准确性方面更好,而二次函数在简单性方面更好。这些步骤对应的公式列在表 6 中。很明显,Alice 执行的手动操作越多,符号公式就越简单(在准确性上稍微牺牲)。KANs 有一个“旋钮”,用户可以调节简单性和准确性之间的平衡(有时简单性甚至可以导致更好的准确性,就像在 GAAM 案例中一样)。
5 相关作品
科尔莫戈洛夫-阿诺德定理与神经网络之间的联系在文献中并不新鲜,但内部函数的病态行为使得科尔莫戈洛夫-阿诺德定理在实践中显得不太有前途。大多数先前的研究都固守于原始的2层宽度为(2n + 1)的网络,这些网络在表现力上受到限制,而且许多甚至是在反向传播之前。因此,大多数研究是基于具有相当有限或人为玩具实验的理论。我们的贡献在于将网络推广到任意宽度和深度,将其重新注入并置于当今深度学习流中,并突出其作为AI +科学基础模型的潜在角色。
神经网络的尺度定律(NSLs)。NSLs 是指测试损失相对于模型大小、数据、计算等呈现为幂律行为的现象。NSLs 的起源仍然神秘,但竞争性理论包括内在维度、任务的量化、资源理论、随机特征、组合稀疏性和最大性。本文通过展示,如果高维函数具有光滑的科尔莫戈洛夫-阿诺德表示,那么这个高维函数令人惊讶地可以作为一维函数进行尺度化(这是人们可以期待的最好的界限)。我们的论文为神经尺度定律带来了新的乐观,因为它承诺了有史以来最快的尺度指数。我们在实验中已经展示了这种快速神经尺度定律可以在合成数据集上实现,但未来的研究需要解决一个问题,即这种快速尺度是否可以用于更复杂的任务(例如语言建模):通用任务是否存在KA表示?如果是,我们的训练是否能在实践中找到这些表示?
机械可解释性(MI)。MI 是一个新兴领域,旨在从机械角度理解神经网络的内在运作。MI 研究可以大致分为被动和主动两种。大多数 MI 研究是被动的,侧重于理解使用标准方法训练的现有神经网络。主动 MI 研究试图通过设计固有可解释的体系结构或开发训练方法来明确鼓励可解释性。我们的工作属于第二类,模型和训练方法通过设计具有可解释性。
可学习的激活函数。在神经网络中,可学习激活函数的想法在机器学习中并不新鲜。可训练的激活函数是以可微的方式学习的,或者以离散的方式搜索。激活函数可以被参数化为多项式、样条、sigmoid线性单元或神经网络。KANs 使用 B-样条来参数化它们的激活函数。我们还在学习激活网络(LANs)上呈现了初步结果,它们的特性介于 KANs 和 MLPs 之间,并将它们的结果推迟到附录 B,以便专注于 KANs 在主要论文中的内容。
符号回归。有许多基于遗传算法(Eureka、GPLearn、PySR)、基于神经网络的方法(EQL、OccamNet)、基于物理启发的方法(AI Feynman)以及基于强化学习的方法的现成符号回归方法。KANs 最类似于基于神经网络的方法,但与先前的工作不同之处在于我们的激活函数在符号捕捉之前是连续学习的,而不是手动固定的。
物理信息神经网络(PINNs)和物理信息神经操作员(PINOs)。在第 3.4 小节中,我们展示了 KANs 可以取代使用 MLPs 来施加 PDE 损失的范式,用于求解 PDEs。我们提到了 Deep Ritz Method、PINNs 用于 PDE 求解,以及 Fourier Neural operator、PINOs、DeepONet 用于学习操作符的学习方法。在所有前述网络中,用 KANs 替换 MLPs 的潜力是巨大的。
数学人工智能。正如我们在第 4.3 小节中看到的那样,最近 AI 已经被应用到结论论中的几个问题中,包括检测一个结是无节点还是一个带有缎带的结,并预测结不变量并揭示它们之间的关系。对于数据科学应用于数学和理论物理数据集的摘要,可参见 [90, 91],对于如何从这些领域的 ML 技术获得严格结果的想法,请参见 [92]。
6 讨论
在本节中,我们从数学基础、算法和应用的角度讨论了 KANs 的局限性和未来方向。
数学方面:尽管我们已经提出了 KANs 的初步数学分析(定理 2.1),但我们对它们的数学理解仍然非常有限。科尔莫戈洛夫-阿诺德表示定理在数学上已经得到了彻底研究,但该定理对应于形状为 [n, 2n + 1, 1] 的 KANs,这是 KANs 的一个非常受限制的子类。我们在更深的 KANs 上的经验成功是否意味着数学上的一些基本内容?一个吸引人的广义科尔莫戈洛夫-阿诺德定理可能定义了超越深度-2组合的“更深”科尔莫戈洛夫-阿诺德表示,并可能将激活函数的平滑性与深度相关联。假设存在一些函数,这些函数在原始的(深度-2)科尔莫戈洛夫-阿诺德表示中无法平滑地表示,但可能在深度-3或更深的情况下平滑地表示。我们是否可以使用“科尔莫戈洛夫-阿诺德深度”的概念来刻画函数类别?
算法方面:我们讨论以下几点:
(1)精度。在架构设计和训练中存在多种选择,尚未充分调查,因此可能的替代方案可以进一步提高精度。例如,可以将样条激活函数替换为径向基函数或其他局部核函数。可以使用自适应网格策略。
(2)效率。KANs 运行缓慢的一个主要原因是不同的激活函数无法利用批处理计算(大量数据通过相同函数)。实际上,可以在激活函数完全相同(MLPs)和完全不同(KANs)之间进行插值,方法是将激活函数分组成多个组(“多头”),组内成员共享相同的激活函数。
(3)KANs 和 MLPs 的混合。KANs 相对于 MLPs 有两个主要区别:
(i)激活函数位于边而不是节点上,(ii)激活函数是可学习的而不是固定的。哪个变化更重要来解释 KAN 的优势?我们在附录 B 中展示了我们的初步结果,我们研究了一个具有(ii)的模型,即激活函数是可学习的(类似于 KANs),但没有(i),即激活函数位于节点上(类似于 MLPs)。此外,还可以构造另一个具有固定激活函数(类似于 MLPs)但位于边上(类似于 KANs)的模型。
(4)适应性。由于样条基函数的内在局部性,我们可以在设计和训练 KANs 中引入适应性,以增强精度和效率:参见多网格方法中的多级训练思想,或者参见多尺度方法中的域相关基函数。
应用方面:我们提供了一些初步证据表明,在科学相关任务中,KANs 比 MLPs 更有效,例如,拟合物理方程和 PDE 求解。我们期望 KANs 也可能有望用于解决 Navier-Stokes 方程、密度泛函理论或任何可以表述为回归或 PDE 求解的任务。我们还希望将 KANs 应用于与机器学习相关的任务,这将需要将 KANs 集成到当前的体系结构中,例如,变压器 - 人们可能会提出“kansformers”,在变压器中用 KANs 替换 MLPs。
KAN 作为 AI + 科学的“语言模型”。大型语言模型之所以具有如此重大的转变性,是因为它们对任何能够说自然语言的人都是有用的。科学的语言是函数。KANs 由可解释的函数组成,因此当一个人类用户盯着一个 KAN 时,就像用函数语言与它交流一样。本段旨在推广 AI-科学家-协作范式,而不是我们具体的工具 KANs。就像人们使用不同的语言进行交流一样,我们期望未来 KANs 将只是 AI + 科学中的一种语言,尽管 KANs 将是使 AI 和人类交流的最初的语言之一。然而,借助 KANs 的帮助,AI-科学家-协作范式变得如此简单和方便,这促使我们重新思考我们希望如何接近 AI + 科学的范式:我们想要 AI 科学家,还是我们想要帮助科学家的 AI?(完全自动化的)AI 科学家的固有难度在于很难使人类偏好量化,这将使人类偏好编码为 AI 目标。事实上,不同领域的科学家对于哪些函数简单或可解释可能有不同的看法。因此,科学家更希望有一个能够使用科学语言(函数)并且可以方便地与单个科学家的归纳偏好进行交互以适应特定科学领域的 AI。
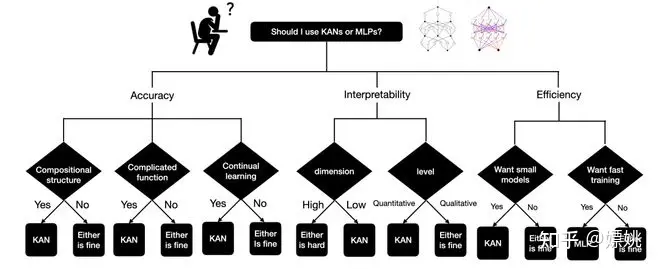
最终的结论:我应该使用 KANs 还是 MLPs?
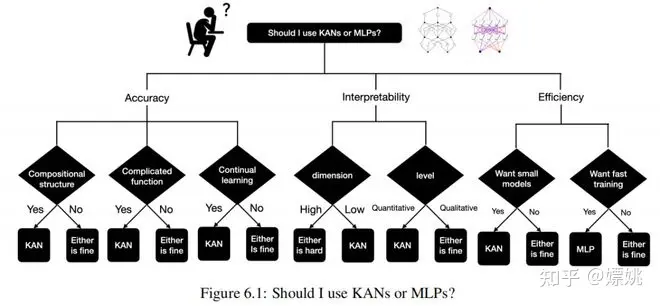
目前,KANs 最大的瓶颈在于训练速度较慢。相同数量的参数情况下,KANs 通常比 MLPs 慢 10 倍。我们应该诚实地说,尽管我们并没有努力优化 KANs 的效率,但我们认为 KANs 的训练速度慢更多地是未来需要改进的工程问题,而不是根本性的限制。如果想要快速训练模型,应该使用 MLPs。然而,在其他情况下,KANs 应该与 MLPs 相比较或更好,这使得值得尝试。图 6.1 中的决策树可以帮助决定何时使用 KAN。简而言之,如果您关心可解释性和/或准确性,并且缓慢的训练不是主要问题,我们建议尝试 KANs。
================ End




