[NOIP2012]开车旅行
[NOIP2012]开车旅行
题目描述
小\(A\) 和小\(B\) 决定利用假期外出旅行,他们将想去的城市从 \(1\)到 \(N\) 编号,且编号较小的城市在编号较大的城市的西边,已知各个城市的海拔高度互不相同,记城市 ii的海拔高度为\(H_i\),城市 \(i\)和城市\(j\)之间的距离 \(d[i,j]\)恰好是这两个城市海拔高度之差的绝对值,即\(d[i,j]=|H_i-H_j|\)。
旅行过程中,小 \(A\)和小 \(B\) 轮流开车,第一天小 \(A\) 开车,之后每天轮换一次。他们计划选择一个城市 \(S\) 作为起点,一直向东行驶,并且最多行驶\(X\) 公里就结束旅行。小\(A\) 和小 \(B\)的驾驶风格不同,小 \(B\)总是沿着前进方向选择一个最近的城市作为目的地,而小\(A\)总是沿着前进方向选择第二近的城市作为目的地(注意:本题中如果当前城市到两个城市的距离相同,则认为离海拔低的那个城市更近)。如果其中任何一人无法按照自己的原则选择目的城市,或者到达目的地会使行驶的总距离超出 \(X\) 公里,他们就会结束旅行。
在启程之前,小 \(A\)想知道两个问题:
- 对于一个给定的 \(X=X_0\),从哪一个城市出发,小\(A\) 开车行驶的路程总数与小\(B\) 行驶的路程总数的比值最小(如果小 \(B\) 的行驶路程为\(0\),此时的比值可视为无穷大,且两个无穷大视为相等)。如果从多个城市出发,小\(A\) 开车行驶的路程总数与小 \(B\)行驶的路程总数的比值都最小,则输出海拔最高的那个城市。
- 对任意给定的 \(X=X_i\)和出发城市\(S_i\),小 \(A\) 开车行驶的路程总数以及小 \(B\)行驶的路程总数。
输入输出格式
输入格式:
第一行包含一个整数 \(N\),表示城市的数目。
第二行有 \(N\)个整数,每两个整数之间用一个空格隔开,依次表示城市 \(1\) 到城市\(N\)的海拔高度,即 \(H_1,H_2,…,H_nH1,H2,…,Hn\),且每个 \(H_i\)都是不同的。
第三行包含一个整数\(X_0\)。
第四行为一个整数 \(M\),表示给定 \(M\)组 \(S_i\)和\(X_i\)。
接下来的 \(M\) 行,每行包含 \(2\) 个整数 \(S_i\)和 \(X_i\),表示从城市\(S_i\)出发,最多行驶 \(X_i\)公里。
输出格式:
输出共\(M+1\)行。
第一行包含一个整数 \(S_0\),表示对于给定的 \(X_0\),从编号为 \(S_0\) 的城市出发,小 \(A\)开车行驶的路程总数与小\(B\) 行驶的路程总数的比值最小。
接下来的 \(M\)行,每行包含\(2\) 个整数,之间用一个空格隔开,依次表示在给定的 \(S_i\)和\(X_i\)下小 \(A\) 行驶的里程总数和小 \(B\) 行驶的里程总数。
输入输出样例
输入样例#1:
4
2 3 1 4
3
4
1 3
2 3
3 3
4 3
输出样例#1:
1
1 1
2 0
0 0
0 0
输入样例#2:
10
4 5 6 1 2 3 7 8 9 10
7
10
1 7
2 7
3 7
4 7
5 7
6 7
7 7
8 7
9 7
10 7
输出样例#2:
2
3 2
2 4
2 1
2 4
5 1
5 1
2 1
2 0
0 0
0 0
说明
【输入输出样例1说明】
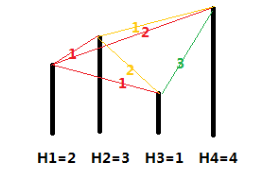
各个城市的海拔高度以及两个城市间的距离如上图所示。
如果从城市 \(1\) 出发,可以到达的城市为 \(2,3,4\)这几个城市与城市 \(1\) 的距离分别为 \(1,1,2\),但是由于城市 \(3\) 的海拔高度低于城市 \(2\),所以我们认为城市 \(3\) 离城市 \(1\) 最近,城市 \(2\) 离城市 \(1\) 第二近,所以小\(A\)会走到城市\(2\)。到达城市\(2\)后,前面可以到达的城市为\(3,4\),这两个城市与城市\(2\)的距离分别为\(2,1\),所以城市\(4\)离城市\(2\)最近,因此小\(B\)会走到城市\(4\)。到达城市\(4\)后,前面已没有可到达的城市,所以旅行结束。
如果从城市 \(2\) 出发,可以到达的城市为 \(3,4\),这两个城市与城市\(2\)的距离分别为 \(2,1\),由于城市 \(3\) 离城市 \(2\) 第二近,所以小\(A\)会走到城市\(3\)。到达城市\(3\)后,前面尚未旅行的城市为\(4\),所以城市\(4\)离城市\(3\)最近,但是如果要到达城市\(4\),则总路程为 \(2+3=5>3\),所以小\(B\)会直接在城市\(3\)结束旅行。
如果从城市 \(3\) 出发,可以到达的城市为 \(4\),由于没有离城市\(3\)第二近的城市,因此旅行还未开始就结束了。
如果从城市 \(4\) 出发,没有可以到达的城市,因此旅行还未开始就结束了。
【输入输出样例2说明】
当 \(X=7\) 时,如果从城市 \(1\) 出发,则路线为\(1 \to 2 \to 3 \to 8 \to 9\),小\(A\)走的距离为\(1+2=3\),小B走的距离为\(1+1=2\)。(在城市\(1\)时,距离小\(A\)最近的城市是\(2\)和\(6\),但是城市\(2\)的海拔更高,视为与城市\(1\)第二近的城市,所以小\(A\)最终选择城市\(2\);走到\(9\)后,小\(A\)只有城市\(10\)可以走,没有第\(2\)选择可以选,所以没法做出选择,结束旅行)
如果从城市\(2\)出发,则路线为\(2 \to 6 \to 7\),小\(A\)和小\(B\)走的距离分别为\(2,4\)。
如果从城市\(3\)出发,则路线为\(3 \to 8 \to 9\),小\(A\)和小\(B\)走的距离分别为\(2,1\)。
如果从城市\(4\)出发,则路线为\(4 \to 6 \to 7\),小\(A\)和小\(B\)走的距离分别为\(2,4\)。
如果从城市\(5\)出发,则路线为\(5 \to 7 \to 8\),小\(A\)和小\(B\)走的距离分别为\(5,1\)。
如果从城市\(6\)出发,则路线为\(6 \to 8 \to 9\),小\(A\)和小\(B\)走的距离分别为\(5,1\)。
如果从城市\(7\)出发,则路线为\(7 \to 9 \to 10\),小\(A\)和小\(B\)走的距离分别为\(2,1\)。
如果从城市\(8\)出发,则路线为\(8 \to 10\),小\(A\)和小\(B\)走的距离分别为\(2,0\)。
如果从城市\(9\)出发,则路线为\(9\),小\(A\)和小\(B\)走的距离分别为\(0,0\)(旅行一开始就结束了)。
如果从城市\(10\)出发,则路线为\(10\),小\(A\)和小\(B\)走的距离分别为\(0,0\)。
从城市\(2\)或者城市\(4\)出发小\(A\)行驶的路程总数与小\(B\)行驶的路程总数的比值都最小,但是城市\(2\)的海拔更高,所以输出第一行为\(2\)。
【数据范围与约定】
对于30%的数据,有\(1≤N≤20,1≤M≤20\);
对于40%的数据,有\(1≤N≤100,1≤M≤100\);
对于50%的数据,有\(1≤N≤100,1≤M≤1,000\);
对于70%的数据,有\(1≤N≤1,000,1≤M≤10,000\);
对于100%的数据,有\(1≤N≤100,000,1≤M≤100,000\) \(-10^9≤H_i≤10^9−10\), \(0≤X_0≤10^9\), \(1≤S_i≤N\),\(0≤X-i≤10^9\),数据保证\(H_i\)互不相同。
这道题主要难在代码实现上面。
NOIP暴力分还是给的很足啊,\(O(n^2)\)的算法很好实现,可以拿到70分。
那么如何在暴力的基础上优化一下拿到满分呢?考虑到当我们确定了起点之后,后面的路径是固定的,那么快速走的方法常见的有路径压缩和倍增,考虑到这道题还有距离的限制,所以我们可以使用倍增。
如何快速处理最近与次近的点
一般的做法有两种:
1.双向链表
2.平衡树(STL set)
我写的是双向链表,但是这种写法一定要在头脑清醒的时候写,不然很容易混,写错了inf次。
具体的处理方法:
1.先把点按高度排序,并记录每个点在排好序的序列中的位置,同时处理好前趋后继。
2.按点编号从前往后处理,最近与次近的点一定在序列的前趋[i],前趋[前趋],后继[i],后继[后继] 的位置。
3.处理完后删除该点(前趋链后继),这样能保证每个点都不会往回走。
倍增
\(f[i][j]\)表示在j点小A和小B都开\(2^i\)天到达的点,这样处理起来更方便,否则如果单独处理需要两个数组,还需要一些判断,很麻烦。
所以我们先单独处理好\(f[0][j]\),然后再常规的递推即可。
还有一点需要注意的是,在往上跳之后,要注意小\(A\)是否可以单独再往前走一步。
貌似不要开long long都能过,数据这么水的么???
#include<bits/stdc++.h>
#define lll long long
using namespace std;
lll read()
{
lll x=0,w=1;char ch=getchar();
while(ch>'9'||ch<'0') {if(ch=='-')w=-1;ch=getchar();}
while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+ch-'0',ch=getchar();
return x*w;
}
const lll N=100010;
double ans=2147483647;
lll n,inf=2147483647,m,x0,x,s,p;
lll next[N],pre[N],pos[N],f[20][N],first[N],second[N];
lll ans1,ans2,sum1[20][N],sum2[20][N];
struct node{
lll v,id;
}c[N];
bool cmp(node p,node q){return p.v<q.v;}
void in()
{
sort(c+1,c+1+n,cmp);
for(lll i=1;i<=n;i++)
{
pre[i]=i-1;next[i]=i+1;pos[c[i].id]=i;
}
for(lll i=1;i<n;i++)
{
lll d1=inf,d2=inf,d3=inf,d4=inf;
lll now=pos[i];
lll qian1=c[pre[now]].id,qian2=c[pre[pre[now]]].id;
lll hou1=c[next[now]].id,hou2=c[next[next[now]]].id;
if(qian1)d1=c[now].v-c[pre[now]].v;if(hou1)d2=c[next[now]].v-c[now].v;
if(qian2)d3=c[now].v-c[pre[pre[now]]].v;if(hou2)d4=c[next[next[now]]].v-c[now].v;
if(d1<=d2)
{
first[i]=qian1;
if(d2<d3) second[i]=hou1;
else second[i]=qian2;
}
else
{
first[i]=hou1;
if(d4<d1) second[i]=hou2;
else second[i]=qian1;
}
pre[next[now]]=pre[now];next[pre[now]]=next[now];
}
}
void init()
{
for(lll i=1;i<=n;i++)
{
f[0][i]=first[second[i]];
sum1[0][i]=abs(c[pos[second[i]]].v-c[pos[i]].v);
sum2[0][i]=abs(c[pos[f[0][i]]].v-c[pos[second[i]]].v);
}
for(lll i=1;i<=19;i++)
{
for(lll j=1;j<=n;j++)
{
f[i][j]=f[i-1][f[i-1][j]];
sum1[i][j]=sum1[i-1][j]+sum1[i-1][f[i-1][j]];
sum2[i][j]=sum2[i-1][j]+sum2[i-1][f[i-1][j]];
}
}
}
void get(lll s,lll v)
{
ans1=0;ans2=0;
for(lll i=19;i>=0;i--)
{
if(v>=sum1[i][s]+sum2[i][s]&&f[i][s])
{
v-=sum1[i][s]+sum2[i][s];
ans1+=sum1[i][s];ans2+=sum2[i][s];
s=f[i][s];
}
}
lll d=abs(c[pos[second[s]]].v-c[pos[s]].v);
if(second[s]&&v>=d) ans1+=d;
}
int main()
{
n=read();
for(lll i=1;i<=n;i++) c[i].v=read(),c[i].id=i;
in();init();
x0=read();
for(lll i=1;i<=n;i++)
{
get(i,x0);
if(ans2)
{
if(1.0*ans1/ans2==ans&&c[pos[i]].v>c[pos[p]].v) p=i;
else if(1.0*ans1/ans2<ans)ans=1.0*ans1/ans2,p=i;
}
}
printf("%lld\n",p);
m=read();
for(lll i=1;i<=m;i++)
{
s=read();x=read();get(s,x);
printf("%lld %lld\n",ans1,ans2);
}
}


