洛谷 P2783 有机化学之神偶尔会做作弊(Tarjan,LCA)
题目背景
LS中学化学竞赛组教练是一个酷爱炉石的人。
有一天他一边搓炉石一边监考,而你作为一个信息竞赛的大神也来凑热闹。
然而你的化竞基友却向你求助了。
“第1354题怎么做”<--手语 他问道。
题目描述
你翻到那一题:给定一个烃,只含有单键(给初中生的一个理解性解释:就是一堆碳用横线连起来,横线都是单条的)。
然后炎魔之王拉格纳罗斯用他的火焰净化了一切环(???)。所有的环状碳都变成了一个碳。如图所示。
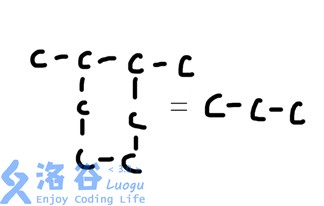
然后指定多组碳,求出它们之间总共有多少碳。如图所示(和上图没有关系)。

但是因为在考试,所以你只能把这个答案用手语告诉你的基友。你决定用二进制来表示最后的答案。如图所示(不要在意,和题目没有什么没关系)。
输入输出格式
输入格式:
第一行两个整数n,m.表示有n个点,m根键
接下来m行每行两个整数u,v表示u号碳和v号碳有一根键
接下来一个整数tot表示询问次数
接下来tot行每行两个整数,a,b表示询问的两个碳的编号
输出格式:
共tot行
每行一个二进制数
输入输出样例
说明
1<n<=10000,1<m<=50000
(两个碳不成环)
这是一道包含了两个板子的题目:tarjan+lca。(应该还是比较明显的)
但是这里我们发现C与C之间必须要连一条双向边,不符合普通tarjan的要求。
我们注意到题目中的条件:两个C不成环。那我们只要让当前的点不递归到它的"爸爸"就可以了。
lca是在树上求两点距离的很常见,常用的办法,在碰到树上题目是可以多考虑。
至于2进制我打的不是很简洁,可以学习一下别人的。
1 #include<bits/stdc++.h> 2 using namespace std; 3 int n,m,cnt,vistime,sum,top; 4 int head[10010],h[10010],dfn[10010],low[10010],s[10010],num[10010],deep[10010],f[10010][23],belong[10010],ans[10010]; 5 bool instack[10010]; 6 struct node{ 7 int to,next; 8 }edge[100010],e[100010]; 9 int read() 10 { 11 int x=0,w=1;char ch=getchar(); 12 while(ch>'9'||ch<'0') {if(ch=='-')w=-1;ch=getchar();} 13 while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+ch-'0',ch=getchar(); 14 return x*w; 15 } 16 void add(int x,int y) 17 { 18 cnt++; 19 edge[cnt].to=y; 20 edge[cnt].next=head[x]; 21 head[x]=cnt; 22 } 23 void ad(int x,int y) 24 { 25 cnt++; 26 e[cnt].to=y; 27 e[cnt].next=h[x]; 28 h[x]=cnt; 29 } 30 void print(int x) 31 { 32 int cnt=0; 33 if(x==0) {printf("0");return;} 34 if(x<0) printf("-"),x=-x; 35 while(x) 36 { 37 cnt++; 38 if(x&1) ans[cnt]=1; 39 x>>=1; 40 } 41 for(int i=cnt;i>0;i--) 42 { 43 printf("%d",ans[i]); 44 ans[i]=0; 45 } 46 printf("\n"); 47 } 48 void tarjan(int,int); 49 void build(int,int,int); 50 int lca(int,int); 51 int main() 52 { 53 int u,v,tot; 54 n=read();m=read(); 55 for(int i=1;i<=m;i++) 56 { 57 u=read();v=read(); 58 add(u,v); 59 add(v,u); 60 } 61 cnt=0; 62 for(int i=1;i<=n;i++) 63 { 64 if(!dfn[i]) 65 tarjan(i,0); 66 } 67 for(int i=1;i<=n;i++) 68 { 69 for(int j=head[i];j;j=edge[j].next) 70 { 71 v=edge[j].to; 72 if(belong[v]!=belong[i]) 73 { 74 ad(belong[i],belong[v]); 75 } 76 } 77 } 78 build(1,0,1); 79 for(int j=1;j<=20;j++) 80 for(int i=1;i<=sum;i++) 81 { 82 f[i][j]=f[f[i][j-1]][j-1]; 83 } 84 tot=read(); 85 for(int i=1;i<=tot;i++) 86 { 87 u=read();v=read(); 88 int LCA=lca(belong[u],belong[v]); 89 print(deep[belong[u]]+deep[belong[v]]-2*deep[LCA]+1); 90 } 91 } 92 void tarjan(int u,int from)//增加参数,防止搜回去 93 { 94 int v; 95 dfn[u]=low[u]=++vistime; 96 s[++top]=u; 97 instack[u]=true; 98 for(int i=head[u];i;i=edge[i].next) 99 { 100 v=edge[i].to; 101 if(v==from) continue; 102 if(!dfn[v]) 103 { 104 tarjan(v,u); 105 low[u]=min(low[v],low[u]); 106 } 107 else if(instack[v]) 108 { 109 low[u]=min(low[u],dfn[v]); 110 } 111 } 112 if(dfn[u]==low[u]) 113 { 114 sum++; 115 do 116 { 117 v=s[top--]; 118 belong[v]=sum; 119 num[sum]++; 120 instack[v]=false; 121 }while(u!=v); 122 } 123 } 124 void build(int k,int fa,int d) 125 { 126 int v; 127 deep[k]=d; 128 for(int i=h[k];i;i=e[i].next) 129 { 130 v=e[i].to; 131 if(v!=fa&&!deep[v]) 132 { 133 f[v][0]=k; 134 build(v,k,d+1); 135 } 136 } 137 } 138 int lca(int x,int y) 139 { 140 if(deep[x]>deep[y]) swap(x,y); 141 for(int i=20;i>=0;i--) 142 if(deep[f[y][i]]>=deep[x]) y=f[y][i]; 143 if(x==y) return x; 144 for(int i=20;i>=0;i--) 145 { 146 if(f[x][i]!=f[y][i]) 147 x=f[x][i],y=f[y][i]; 148 } 149 return f[x][0]; 150 }


