1.本周学习总结(0--2分)
1.1思维导图

1.2谈谈你对图结构的认识及学习体会。
图结构,它不再像线性表和树结构那样数据之间存在一对一或一对多的关系,它是数据的多对多的一种表现,在用代码表示上,它可以用邻接表和邻接矩阵来写:邻接矩阵,感觉就是二维数组,书本运用了用了两个结构体,一个是顶点的类型,而另一个是完整的图邻接矩阵类型;而邻接表就是不同于邻接矩阵关于图的另外一种表示,书本上运用了三种结构体,也在结构体中运用了一个结构体指针,相较于邻接表来说较难理解,这三个结构体一个用来存放头节点,一个用来存放后续结点,而剩下的就是存放完整的图邻接表。这两种表示存储结构各有各的特点,关于图的遍历分为深度与广度,深度遍历和广度遍历一个运用在图中唯一一次的遍历,一个运用了队列,比起后面的生成树与最短路径简单一些,而生成树可以由普里姆算法和克鲁斯卡尔算法来实现,普里姆算法与贪心算法相类似,只不过还用了一个数组来存放候选边,而克鲁斯卡尔算法则是将最短路径先选出来,然后再连起来。对于这两种算法,看一下还是勉强能懂的,但要写肯定写不出来。
2.PTA实验作业(6分)
2.1.题目1:7-1 图着色问题

2.1.1设计思路
宏定义数组visited并将初值置为0,定义数组d来储存路径;
宏定义二维数组a[501][501]来存储图的边
void dfs(int i)
定义 j;
d[k++]=i;
标记结点已遍历;
for j=1 to v do
if 存在边 且 结点未被访问 then
dfs(j);
end if
end for
void dfs1()
定义 i;
for i=1 to v
if 结点未被访问 then
dfs(i);
end for
int main()
输入v、e、z;
输入存在的边,并在二维将二维矩阵置为1;1
调用dfs1函数;
输入n;
while n--
初始化 b[501]={0},c[501],e[501],sum=0,flag=1;
for i=1 to v;i++)
输入c[i];
b[c[i]]++;
if b[c[i]]等于1 then sum++;
end for
if sum不等于z then
flag=0;
end if
for i=0 to k do
e[i]=c[d[i]];
end for
for i=0 to k
forj=0 to k
if a[d[i]][d[j]]等于1并且e[i]等于e[j] then
flag=0;
break;
end if
if flag等于0 then break;
end for
if flag等于0 then
输出No
end if
else
输出Yes
end
return 0
2.1.2代码截图

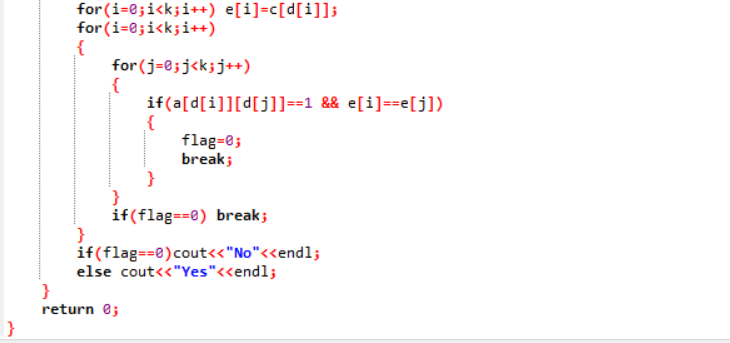
2.1.3本题PTA提交列表说明。

1.老师上课讲过要用深度遍历来写,然后看完课本后来写这道题,多加了一个递归口,导致程序没有完全执行完就停止了;
2.写完深度遍历的那一部分,没有完全懂这道题的思路,然后上网查了一下,理解了一遍来写,还是有一些小细节没做好。
2.2 题目2:7-3 六度空间
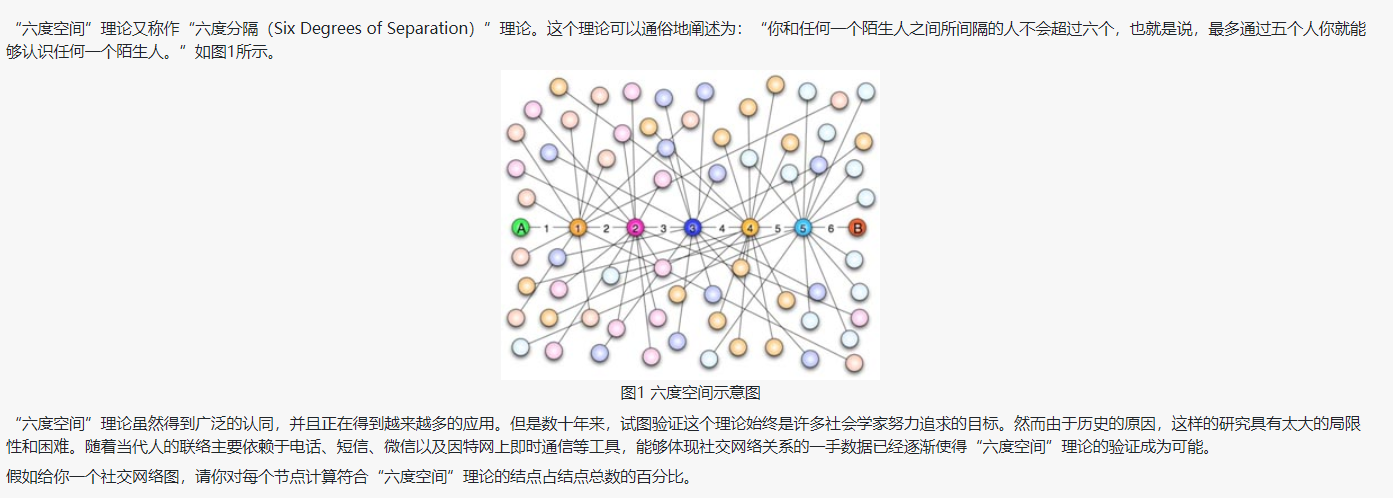
2.2.1设计思路
宏定义visit数组存放被访问过的结点
宏定义二维数组arr来存放边的信息
int BFS(int v) //先使用广度遍历,然后记录在范围在六个之间的结点个数
新建整型队列q;
定义level存放结点距离, 定义tail存放与需要访问结点相关的结点, 定义last暂时存放需要遍历的结点, 定义count存放相关结点个数;
需要访问的结点入队;
标记结点已经被访问;
while 队列不空 do
取队尾元素;
出队;
for i=1 to N do
if 两个结点之间存在边 且 第二个顶点没被访问过 then
相关结点个数加一;
tail = i;
标记结点已经被访问;
出队;
end if
if temp == last then
level++; //结点距离加一
last = tail; //last下移到下一个相关结点
end if
if level == 6 then break;//如果结点距离超过六,退出循环
end
return count;
int main()
输入N,M;
输入邻接表信息;
for i=0 to N then
使用BFS函数计算;
初始化visit数组;
输出;
return 0;
2.2.2代码截图
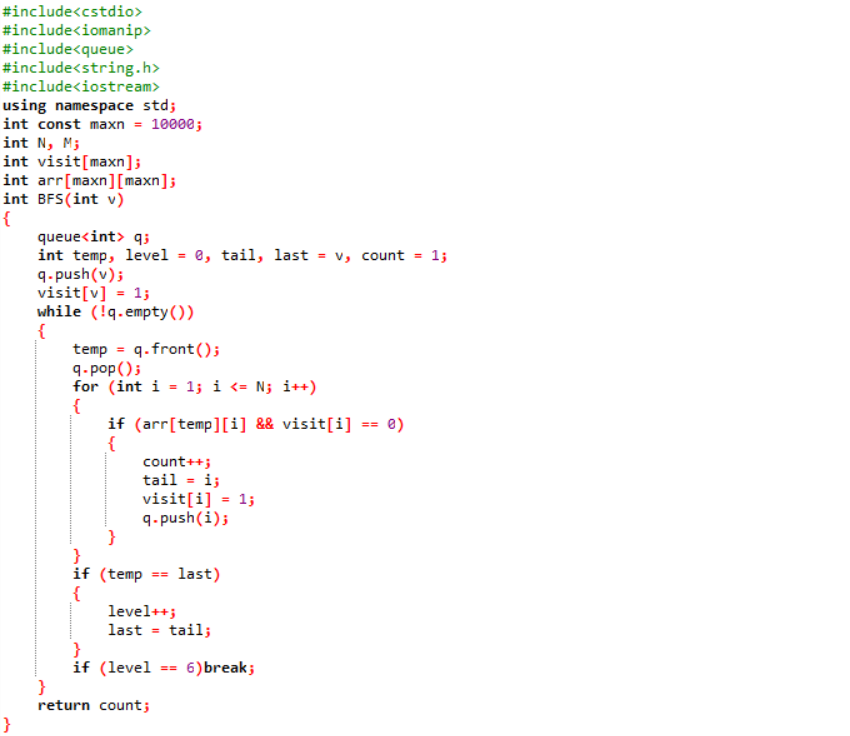
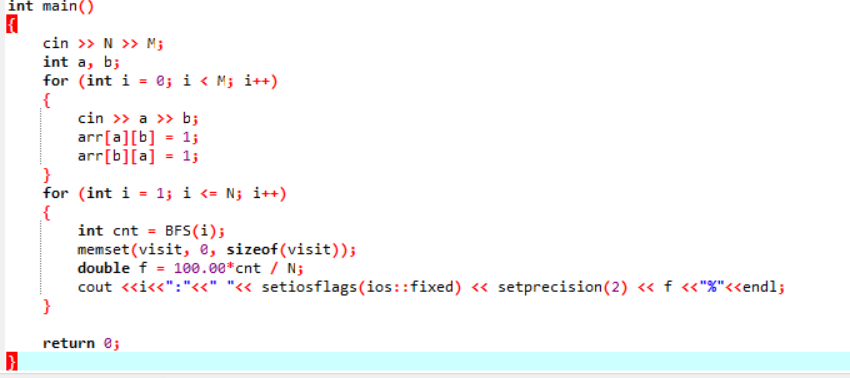
2.2.3本题PTA提交列表说明。
1.老师上课讲到这道题时,讲到要用上广度遍历,自己敲的时候,还是把广度遍历的算法敲错了,导致程序运行不来;
2.后面思考怎么统计结点个数时,想到用数组来记录个数,但是退出程序时的那个条件出错了,导致输出的结点只到8,9,后面改了循环条件,发现还是没有完全输出,又看了看建图函数,发现里面的循环条件出错了,导致间的图不完全。
3.输出是不知道c++如何精确到小数点后两位,后来百度了一下,可以用etiosflags(ios::fixed) << setprecision(2) 来写。
2.3 题目3:7-4 公路村村通

2.3.1设计思路
宏定义Minimum无穷大
宏定义二维数组Map存放边的信息
宏定义visit数组存放被访问过的结点
宏定义lowcos存储每个顶点与之相连边的权值
int prim()
int i,j,k;
int sum =0,flag=0;
标记结点已经被访问;
权值初始化
for i=2 to n do
Min = Minimum;
for j=1 to n then //寻找每个顶点与之相连的边的最小权值
if !visit[j]&&lowcost[j]<Min then
Min = lowcost[j];
k=j;
end for
if Min==Minimum then //如果某个顶点与之相连的边找不到最小权值,则表示道路不通
flag = 1;
break;
sum+=Min;
标记结点已经被访问;
for j=1 to n do //纠正权值
if !visit[j]&&lowcost[j]>Map[j][k] then
lowcost[j]=Map[j][k];
if flag==0 //存在公路
输出sum;
else
输出-1;
int main()
while cin>>n>>m do
为map与visit置初值;
初始化map
调用prim函数
return 0;
2.3.2代码截图
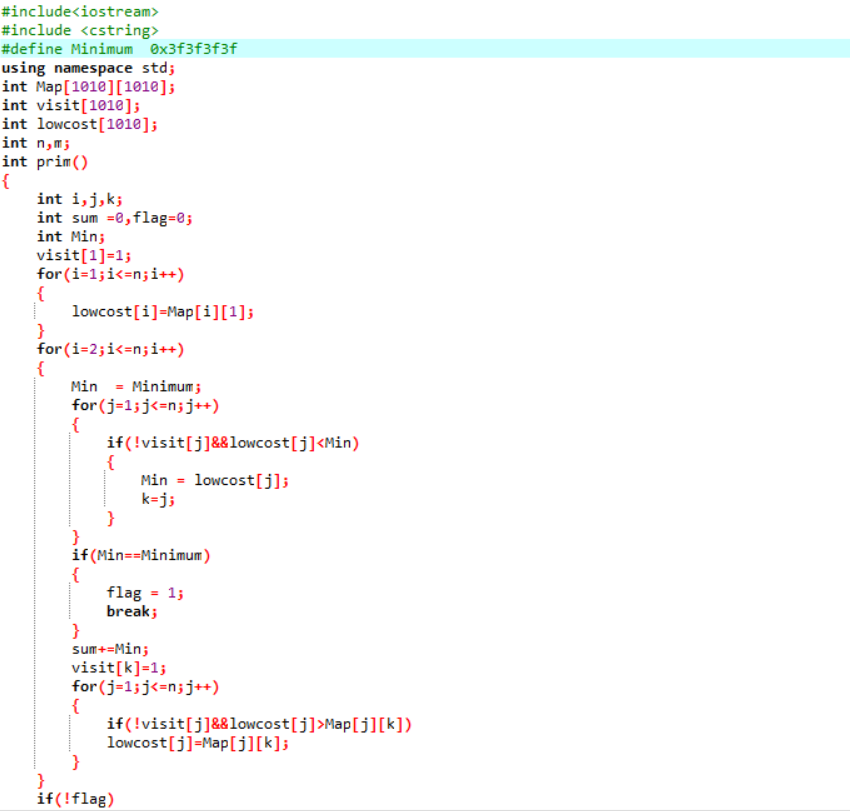

2.3.3本题PTA提交列表说明。

1.不知道无法畅通的情况怎么处理,后来又定义了一个无穷大的变量与最小的路径进行标胶,如果最小的路径等于无穷大,则说明没有路径即无法正常畅通。
2.这道题是使用prim来写,当时还是在没有完全掌握prim算法上来写,没把候选边的那一部分写上去。
3、上机考试错题及处理办法
3.1.
题目:
6-1 jmu-ds-最短路径

错误代码:

错的原因:
由于pta上的图的作业集没有这道题,然后就没认真看,当时写这道题的时候完全是按照老师讲课时的印象写的,和根据自己印象中的prim算法写的,结果当然是错的。考完后又看了看书本,按照理解再敲了一遍。
处理方法:

3.2
题目:
7-2 公路村村通
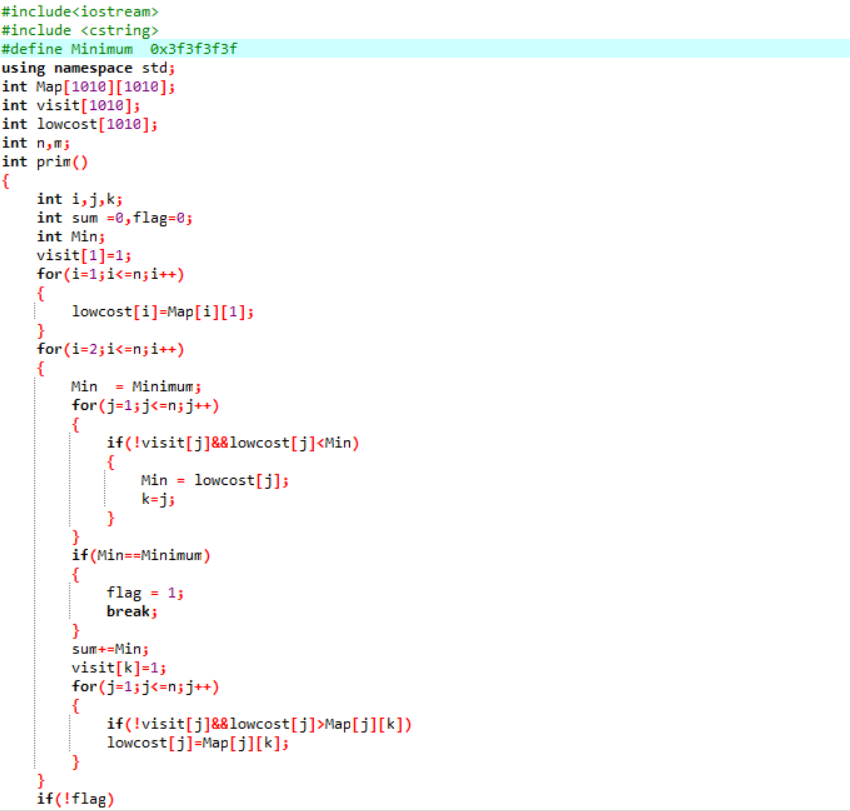
错误代码:

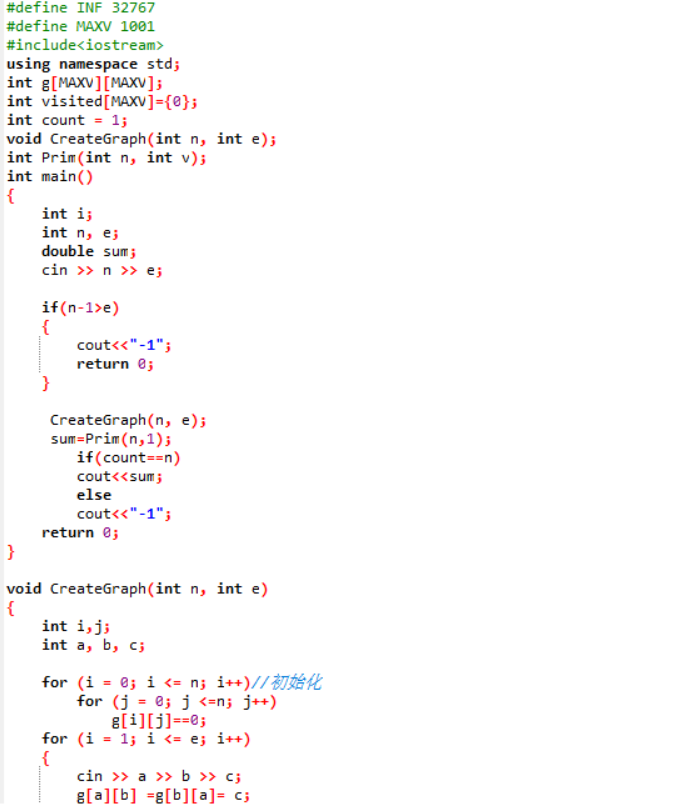

错的原因:
这道题是根据舍友提供的思路来敲的,后来百度了这一道题,发现自己在处理prim算法时发现时间复杂度过大,导致答案输不出来。
处理方法:

3.3
7.3
在考试时还没来得及做
#include<bits/stdc++.h>
using namespace std;
#define INF 0x3f3f3f3f
const int maxn = 503;
int n,m,s,en;
bool vis[maxn];
int dis[maxn];
int pre[maxn];
int cnt[maxn];
struct node
{
int v,c,di;
node()
{
v = c = di = 0;
}
node(int a,int b)
{
v = a;
c = b;
di = 0;
}
node(int a,int b,int cc)
{
v = a;
c = b;
di = cc;
}
bool operator<(const node &a)const
{
return c>a.c;
}
};
vector<node>vec1[maxn];//dis
vector<node>vec2[maxn];//time
priority_queue<node> que;
void addEdge1(int u,int v,int w,int x)
{
vec1[u].push_back(node(v,w,x));
}
void addEdge2(int u,int v,int w,int x)
{
vec2[u].push_back(node(v,w,x));
}
void dijkstra2()
{
for(int i=0; i<n; i++)
pre[i] = i;
memset(vis,false,sizeof(vis));
for(int i=0; i<=n; i++)
{
dis[i] = INF;
cnt[i] = 0;
}
while(!que.empty())
que.pop();
dis[s] = 0;
pre[s] = -1;
cnt[s] = 0;
que.push(node(s,0));
node tmp;
while(!que.empty())
{
tmp = que.top();
que.pop();
int u = tmp.v;
if(vis[u])continue;
vis[u] = true;
int l = vec2[u].size();
for(int i=0; i<l; i++)
{
int v = vec2[u][i].v;
int cost = vec2[u][i].c;
int juli = vec2[u][i].di;
if(!vis[v] && dis[v] > dis[u]+cost)
{
cnt[v] = cnt[u]+juli;
dis[v] = dis[u] + cost;
pre[v] = u;
que.push(node(v,dis[v]));
}
else if(!vis[v] && dis[v] == dis[u]+cost)
{
if(cnt[v] > cnt[u] + juli)
{
pre[v] = u;
cnt[v] = cnt[u]+juli;
}
}
}
}
}
void dijkstra1()
{
for(int i=0; i<n; i++)
pre[i] = i;
memset(vis,false,sizeof(vis));
for(int i=0; i<=n; i++)
{
dis[i] = INF;
cnt[i] = INF;
}
while(!que.empty())
que.pop();
dis[s] = 0;
pre[s] = -1;
cnt[s] = 1;
que.push(node(s,0));
node tmp;
while(!que.empty())
{
tmp = que.top();
que.pop();
int u = tmp.v;
if(vis[u])continue;
vis[u] = true;
int l = vec1[u].size();
for(int i=0; i<l; i++)
{
int v = vec1[u][i].v;
int cost = vec1[u][i].c;
if(!vis[v] && dis[v] > dis[u]+cost)
{
cnt[v] = cnt[u]+1;
dis[v] = dis[u] + cost;
pre[v] = u;
que.push(node(v,dis[v]));
}
else if(!vis[v] && dis[v] == dis[u]+cost)
{
if(cnt[v] > cnt[u] +1)
{
pre[v] = u;
cnt[v] = cnt[u]+1;
}
}
}
}
}
bool panduan(int s1[],int s2[],int a,int b)
{
if(a != b)
return false;
for(int i=0; i<a; i++)
{
if(s1[i] != s2[i])
return false;
}
return true;
}
int main()
{
//freopen("in.txt","r",stdin);
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
//freopen("in.txt","r",stdin);
cin>>n>>m;
int a,b,c,d,e;
for(int i=0; i<m; i++)
{
cin>>a>>b>>c>>d>>e;
if(c == 0)
{
addEdge1(b,a,d,e);
addEdge2(b,a,e,d);
}
addEdge1(a,b,d,e);
addEdge2(a,b,e,d);
}
// for(int i=0;i<vec1[3].size();i++)
// cout<<"is : "<<vec1[3][i].c<<" ";
cin>>s>>en;
dijkstra2();
int ss1[maxn];
int ss2[maxn];
int now = en;
int pos1 = 0,pos2 = 0;
int dis1 = dis[en];
while(pre[now] != -1)
{
ss1[pos1++] = now;
now = pre[now];
}
dijkstra1();
now = en;
while(pre[now] != -1)
{
ss2[pos2++] = now;
now = pre[now];
}
if(panduan(ss1,ss2,pos1,pos2))
{
cout<<"Time = "<<dis1<<"; ";
cout<<"Distance = "<<dis[en]<<": ";
cout<<s;
for(int i=pos2-1; i>=0; i--)
cout<<" => "<<ss2[i];
cout<<endl;
return 0;
}
cout<<"Time = "<<dis1<<": ";
cout<<s;
for(int i=pos1-1; i>=0; i--)
cout<<" => "<<ss1[i];
cout<<endl;
cout<<"Distance = "<<dis[en]<<": ";
cout<<s;
for(int i=pos2-1; i>=0; i--)
cout<<" => "<<ss2[i];
cout<<endl;
return 0;
}



