二维数组的子数组和最大问题(李帅 张硕)

 题目要求：

程序要使用的数组放在一个叫 input.txt 的文件中,  文件格式是:

数组的行数,

数组的列数,

每一行的元素,  (用逗号分开)

每一个数字都是有符号32位整数, 当然, 行数和列数都是正整数。

例如下面的文件说明数组是有1行, 6列, 元素依次是:  5, 6, –3, 8, –9, 2

 

 

看到这道题，首先想到的应该是枚举法，找到所有的子数组，并求和，寻出最大值，关键问题就是如何找出所有的子数组。

一开始的想法是，从第一个数开始找出所有包含这个数的矩形，然后往后依次类推，但显然算法并不好写。应该尽量找简单点的算法。由此想到一维数组，用上一道题的算法来实现，虽然变成了二维数组，但还是可以看成一维数组的，下面举例说明一下算法。

 

 

以list[3][4]为例：

 

我们可以将每一列看成一个数，也就是求和分别为sum[0],sum[1],sum[2],sum[3].

从第一行开始：

第一次循环sum[0],sum[1],sum[2],sum[3].分别为第一行每列的和。以一维数字的方法很容易寻出子数组的最大和。

 

第二次循环sum[]分别为第一行和第二行的和，也就是景两行合并相加，在以一维的方法进行比较比较。

   。

   。

   。

直到所有行合并之后得到一个最大值。然后将sum[]赋值为0；

然后从第二行开始：

第一次循环sum[0],sum[1],sum[2],sum[3].分别为第二行每列的和。以一维数字的方法很容易寻出子数组的最大和。

 

第二次循环sum[]分别为第二行和第三行的和，也就是景两行合并相加，在以一维的方法进行比较比较。

   。

   。

   。

直到除第一行外所有行合并之后得到一个最大值。然后将sum[]赋值为0；

以此往下运行，直到第一次循环是最后一行.....

至于写入文件并不算困难，就不多说了。

源代码如下

#include<iostream>
#define maxnum 100
using namespace std;
FILE * input;
int main()
{
    int list[maxnum][maxnum];
    int l,c;
    input=fopen("input.txt","w");
    cout<<"请输入数组的行数:"<<endl;
    cin>>l;
    fprintf(input,"%d\n",l);
    cout<<"请输入数组的列数:"<<endl;
    cin>>c;
    fprintf(input,"%d\n",c);
    for(int h=0;h<l;h++)
    {
        for(int k=0;k<c;k++)
        
        {
            cin>>list[h][k];
            fprintf(input,"%d,",list[h][k]);
        }
        fprintf(input,"\n");
    }

    int sum[maxnum],sumk=0;
    int max=list[0][0];
    //初始化sum[]
    
    for(int z=0;z<l;z++)
    {
        for(int j=0;j<c;j++)
        {
            sum[j]=0;
        }
        for(int i=z;i<l;i++)
        {
            for(int j=0;j<c;j++)
            {
                sum[j]=sum[j]+list[i][j];
            }
            
            for(int m=0;m<l;m++)
            {
                sumk=0;//初始化sum
                for(int n=m;n<c;n++)
                sumk=sumk+sum[n];
                if(max<sumk)
                {
                    max=sumk;
                }
            }
            

        }
    }
    cout<<"数组中最大的子数组的和为："<<max<<endl;
    fclose(input);
    return 0;
}

 

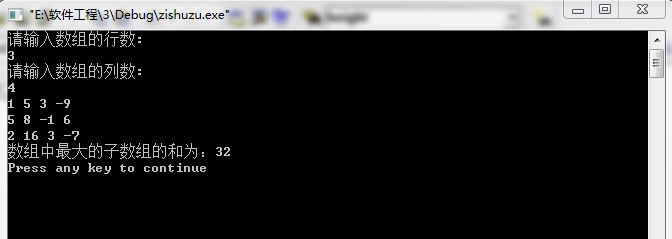
运行结果：