费用流
在最大流中,每条边只有一个容量参数。如果再加上一个费用,就成为了费用流。
下面借助例题来理解费用流:
简化版题意:
给定一个网络。每条边有容量 \(w_i\) 与费用 \(c_i\),代表这条边的最大流量为 \(w_i\),每流一个单位需要花费 \(c_i\)。
求出这个网络的最大流,以及所有最大流中费用最小的一个流的费用。
费用流的常用解决方法是最大流 \(+\) 最短路。
在最大流的 Edmonds-Karp 算法中,我们使用 BFS 来求路径。在费用流中,我们可以使用 SPFA 求一条费用最小的路径,然后再计算该路径的最大流。这样不断求路径,直到没有路径,就可以求出最小费用了。
在建反向边时,反向边的权值应为正向边权值的相反数,这和最大流中反向边流量的原理相同。
时间复杂度如何?设总流量为 \(F\),每条路径至少有一个流量,每次 SPFA 的时间复杂度为 \(\mathcal{O}(NM)\),因此时间复杂度为 \(\mathcal{O}(FNM)\)。显然 SPFA 一般情况下是不会达到上界的,除非遇到某人。
比如下面的第一个例题,总流量为 \(2\),因此时间复杂度为 \(\mathcal{O}(2NM)\)。
下面给出例题的代码:
费用流有很多应用。下面给出几种应用:
因为是无向图,所以从终点到起点与从起点到终点是相同的。题目也就变为从起点到终点走两次,每条边只能走一次,求最短路。
如果采用贪心法,先走一次最短路,然后删除这些边,再走一次最短路,那么可能会出现错误。如下图:
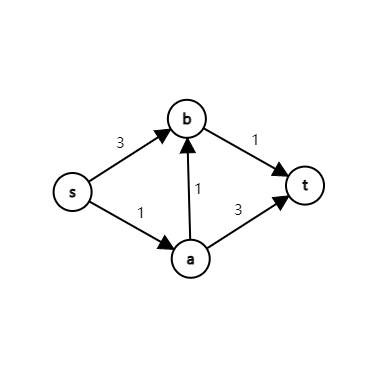
删除边后,图不连通,无法求最短路。
该题可以用费用流求解。
每条边的流量为 \(1\),代表只能走一次。建一个超级源点 \(s\) 与一个超级汇点 \(t\),\(s \to 1\) 与 \(n \to t\) 之间都有一条流量为 \(2\),费用为 \(0\) 的边,代表可以走两次。接下来计算费用流即可。
方格取数问题可以使用费用流求解。
但是有个问题:在费用流中边只能走一次,而本题中点的权值只能计算一次。那该怎么办呢?
本题可以使用入出点的技巧。为每个点设一个入点和一个出点,每个点的入点连向出点,出点连向其他点的入点。
入点连向出点两条边,一条的流量为 \(1\),费用为该点的权值,代表只能计算一次;另一条的流量为 \(2\),费用为 \(0\),代表不计算该点权值。出点连向入点一条流量为 \(2\),费用为 \(0\) 的边。再用一个超级源点 \(s\) 和超级汇点 \(t\),连边方式与上题相同。那么这道题就做出来了。
还需要注意的是本题为最大费用最大流,即用 SPFA 求的是最长路。



