最大流
最大流问题是网络流中的基本问题,它基于有向图。通过下面的例题引出最大流的定义。
该例题并没有讲解最大流的定义,可以参考下面的例题:
如下图:
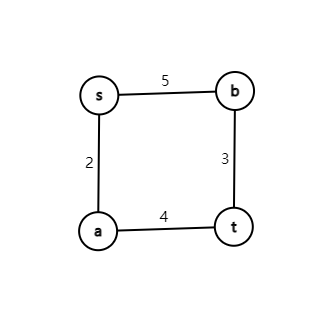
一条路径的最大流量为这条路径中容量最少的边的容量。
在这张图中,从 \(s\) 到 \(t\) 有两条路径:\(s \to a \to t\) 的最大流量为 \(2\),\(s \to b \to t\) 的最大流量为 \(3\)。因此最大流为 \(5\)。
形象一点的说:将每条边的流量理解为这条边的最多经过次数。然后从起点到终点找路径,最大流即为能找出路径的最多数量。
常用的最大流算法有 Edmonds-Karp,Dinic,ISAP 三种算法。第一种算法的实现简单,但效率不高。后两种算法的代码长度差不多,但 ISAP 比 Dinic 要快,是最大流问题的首选算法。
下面用 Ford-Fulkerson 方法介绍最大流的基本问题。
1 Ford-Fulkerson 方法
1.1 Ford-Fulkerson 的思路
它的思路不难理解。主要分为以下三步:
-
寻找从 \(s\) 到 \(t\) 的路径
-
更新每条边的残留容量
-
重复步骤 \(1\),直到没有路径了
在上图中,找完路径后的残留网络应该如下图:
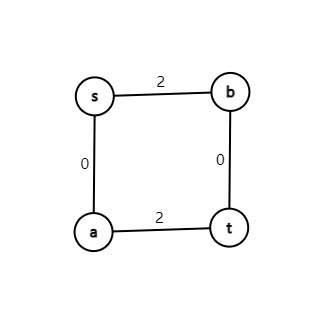
流量为 \(0\) 的边相当于没有边。
但是如果直接寻找在更新可能会产生错误。比如这张图:
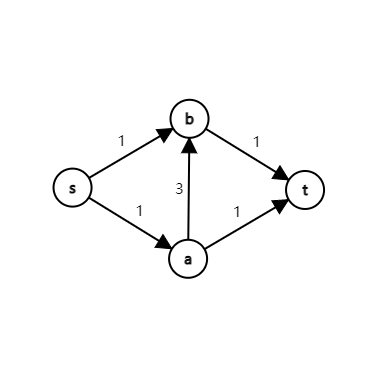
如果第一次找到了 \(s \to a \to b \to t\) 这条路,那么更新后不再有路径了,求得的最大流为 \(1\)。实际上最大流应为 \(2\)。
解决方法为:如果找到的路径包含 \(a \to b\) 这条边,那么在更新时连一条 \(b \to a\) 的边,容量为这条路径的最大流(如果已经有这条边,则将这条边的容量加上这条路径的最大流)。
在上图中,如果运用这种方法,那么新的求解的过程如下:
- 找到 \(s \to a \to b \to t\) 的路径,最大流为 \(1\),更新残留网络:
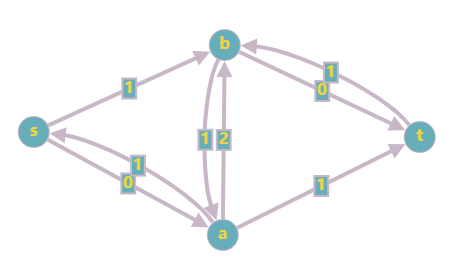
去掉流量为 \(0\) 的边:
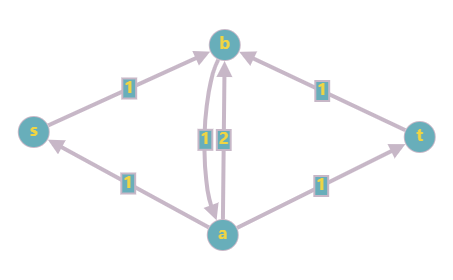
- 找到 \(s \to b \to a \to t\) 的路径,最大流为 \(1\),更新残留网络:
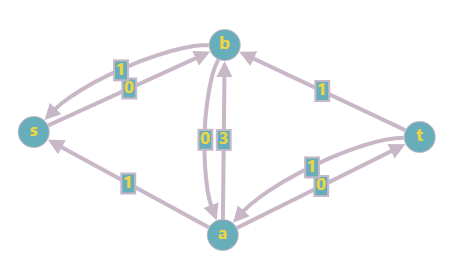
去掉流量为 \(0\) 的边:
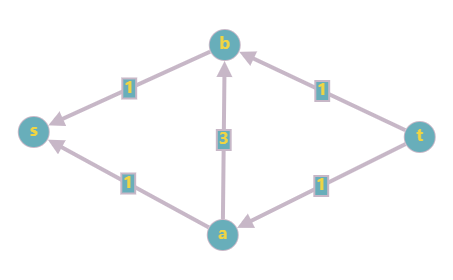
此时没有路径了,最大流为 \(2\)。
为什么这种方法是对的呢?
就以上图为例子:
在 \(s \to a \to b \to t\) 和 \(s \to b \to a \to t\) 这两条路径中,前者包含 \(a \to b\),后者包含 \(b \to a\),这刚好是一对反向边。
那么这就相当于:我可以先走第一条路的 \(s \to a \to b\) 部分,再走第二条路的 \(b \to a \to t\) 部分。也就是走到 \(a\),然后走到 \(b\),再回到 \(a\)。假设从 \(a\) 走到 \(b\) 流了 \(f\) 的流量,那么我们需要再流回来 \(f\) 的流量,因此需要建这样的反向边。另一条路同理。
简而言之,就是我以后可能不走这条路,所以我还要再流回来。
为了能这么走,我们就可以连反向边。在费用流中,反向边的费用是正向边费用的相反数也是运用了这个原理。
1.2 Ford-Fulkerson 方法的实现
在搜索路径时,可以使用 DFS 或 BFS。但是 DFS 可能陷入长时间的迭代。如下图:
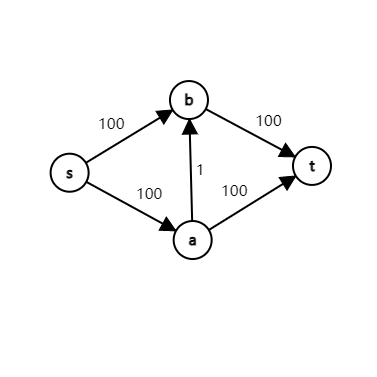
如果 DFS 第一次走了 \(s \to a \to b \to t\) 的路,那么更新后如下:
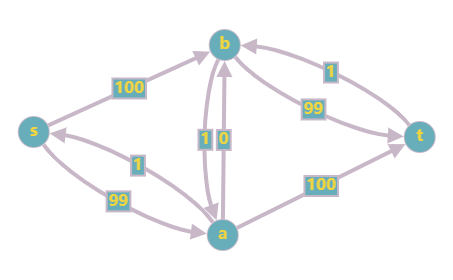
接下来走 \(s \to b \to a \to t\),更新后如下:
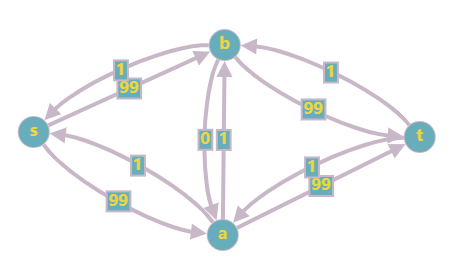
可以发现,DFS 每次会选择一条流量为 \(1\) 的路径,这样一共会选择 \(200\) 次。如果用 BFS,几次就够了。
2 Edmonds-Karp 算法
Edmonds-Karp 算法就使用 BFS 寻找路径。
那么时间复杂度如何呢?
可以发现,最多有 \(NM\) 条路径,一条路径的长度最多为 \(M\),因此时间复杂度为 \(\mathcal{O}(NM^2)\),但实际上远远达不到这个数值,大约可以处理 \(10^4\) 的网络。
下面给出 洛谷-P3376 的代码:
3 Dinic 算法
Edmonds-Karp 算法每次 BFS 后只处理一条路径。能否同时处理多条路径?这就是 Dinic 算法的思想。
同时处理多条路径可以用 DFS 实现。每次 BFS 时,同时处理该点到起点经过边的数量 \(dep\),每次 DFS 时,只搜索 \(dep_v=dep_u+1\) 的点,并更新这条边的残余流量。除此之外,还有两个优化技巧:
- 当前弧优化
在 DFS 中遍历出边时,可以记录当前到达了哪条出边,这样在下次搜索到这个点时,直接从上次遍历到的点开始即可。
用一个 \(now\) 数组。初始时 \(now_u=hd_u\),在 DFS 遍历出边时,每次更新 \(now_u\),直到没有流量或者没有出边后停止。
- 丢弃没有路径了的点
如果在搜索时 \(v\) 到 \(t\) 的流量为 \(0\) 了,那么直接修改 \(dep_v=0\),这样以后不会再到达 \(v\) 了。
由于是链式前向星,如果直接找反向边会比较麻烦,这里运用奇偶边的技巧:
第一条边从编号 \(2\) 开始存。每对正反边中,正向边的编号为偶数,反向边的编号为奇数。如果正向边的编号为 \(i\),那么 \(i \operatorname{xor} 1\) 就是对应的反向边,\((i+1) \operatorname{xor} 1\) 就是对应的正向边。
4 ISAP 算法
Dinic 用了多次 BFS,而 ISAP 只用一次,因此比 Dinic 快。
ISAP 的思想为记录每个点到 \(t\) 的距离,每次只寻找 \(dep_v=dep_u-1\) 的点。如果没有这样的点了,就更新 \(dep_u\) 来继续寻找。更新时设 \(v\) 为 \(u\) 能到达的点(不包括没有流量的边),则 \(dep_u \gets \min\{dep_v\}+1\),即所有有流量的出点中深度最浅的点的深度 \(+1\)。
ISAP 也有两个优化技巧:
- 当前弧优化
方法同 Dinic。
- 间隙优化
设 \(gap_i\) 表示深度为 \(i\) 的点的个数。每次没有找到出边时,如果 \(gap_{dep_u}=0\),说明图出现断层,直接结束即可。
因为要更新 \(dep\),DFS 不好处理,因此每次只找一条路径,这样就需要记录前驱了。在寻找时可以使用比递归快的循环。
下面给出 ISAP 的代码:



