线段树
1. 线段树的概念
线段树就是分治 \(+\) 二叉树 \(+\) Lazy-Tag。下图是一个包含 \(10\) 个元素的线段树。
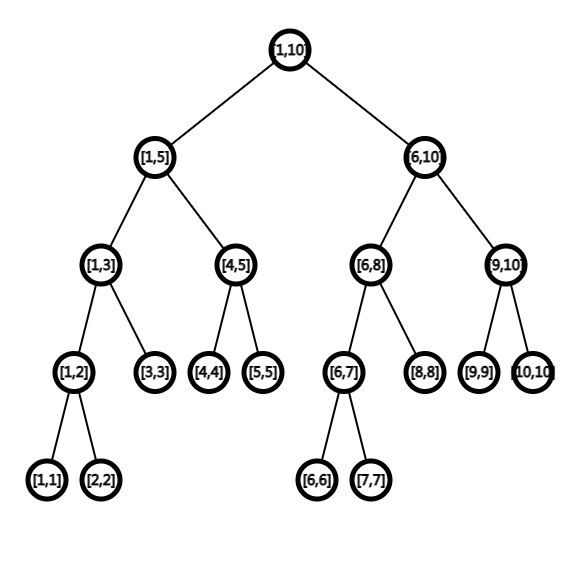
观察这棵树,它的基本特征如下:
-
用分治从上向下建树。每次分治,左右子树各有一半。
-
每个结点都表示一个区间。非叶子节点表示的区间有多个元素,叶子节点表示一个元素。
-
除了最后一层,其他层都是满的。这种二叉树最平衡,效率最高。
对于一个区间 \([l,r]\):
-
若 \(l=r\),说明这个区间只有一个元素。那么它是一个叶子结点。
-
否则它有多个元素。设 \(mid=\lfloor \frac{l+r}{2} \rfloor\),则它的左儿子区间为 \([l,mid]\),右儿子区间为 \([mid+1,r]\)。如 \(l=1,r=5\),则 \(mid=3\),左儿子区间为 \([1,3]\),右儿子区间为 \([4,5]\)。
每个结点的值都代表了这个结点的子树的值(如区间和,区间最大值)。这样在修改或查找整个区间时,只需要访问根节点即可。而线段树有 \(\log N\) 层,因此在查找一个区间时,只需要 \(\log N\) 次就能找到,可以大大提高效率。
那么在构造线段树时,如果有 \(N\) 个数,那么往往需要开到 \(4N\) 个结点。下面说明原因。假设有 \(N=2^k+1\) 个数,那么最后一行只有一个结点,倒数第二行有 \(N\) 个结点,第一个结点为区间 \([1,2]\),后面的第 \(i\) 个结点为第 \(i+1\) 个元素。最后一行就有 \(2N\) 个结点。而第一行至倒数第三行一共有 \(N-1\) 个结点,因此最后需要 \(N+2N+N-1 \approx 4N\)。
下面给出建树与更新结点的代码,以区间和为例。
/* 静态数组版 */
const int N(1e5+5);
ll a[N],t[N<<2];
/*a是原数组,t是线段树数组*/
int ls(int p){
return p<<1;
/*p的左儿子编号为p*2,即p<<1*/
}
int rs(int p){
return p<<1|1;
/*p的右儿子编号为p*2+1,即p<<1|1*/
}
void push_up(int p){
/*更新节点p的去间和*/
t[p]=t[ls(p)]+t[rs(p)];
/*左儿子的区间和+右儿子的区间和*/
}
void build(int p,int l,int r){
/*对a数组的[l,r]建树,根为p*/
if(l==r){
/*到达叶子*/
t[p]=a[l];return;
/*只有一个元素*/
}
int mid=(l+r)>>1;
build(ls(p),l,mid);
build(rs(p),mid+1,r);
/*左右儿子分别建树*/
push_up(p);
/*更新区间和*/
}
/* 指针动态开点版 */
vector<ll> a;
/*原数组*/
struct node{
ll sum,lz;
unique_ptr<node> ls,rs;
/*sum为区间和,lz为以后要用到的懒标记,ls rs分别为左右儿子的指针,用unique_ptr安全指针存储*/
/*unique_ptr的每个元素只能被一个指针指向,所以后面所有函数在传入节点指针时都要传址*/
};
unique_ptr<node> root;
/*根节点指针*/
void push_u(unique_ptr<node> &u){
u->sum=u->ls->sum+u->rs->sum;
/*更新区间和,为两个子区间的区间和之和*/
}
void build(unique_ptr<node> &u,usi l,usi r,vector<ll> &a){
/*对a数组的[l,r]建树,根为u*/
u=make_unique<node>();
/*为u新开一个节点*/
if(l==r){
/*是叶子结点,只有一个元素,所以区间和就是a[l]*/
u->sum=a[l];
u->lz=0;
/*没有懒标记*/
return;
}
usi mid((l+r)>>1);
build(u->ls,l,mid,a);
build(u->rs,mid+1,r,a);
/*对左右儿子分别建树*/
push_u(u);
/*更新区间和*/
}
2. 区间查询
将数列 \(\{1,4,5,8,6,2,3,9,10,7\}\) 建树。如下图(左边是节点编号;上图右边是代表区间,下图右边是结点的值)。
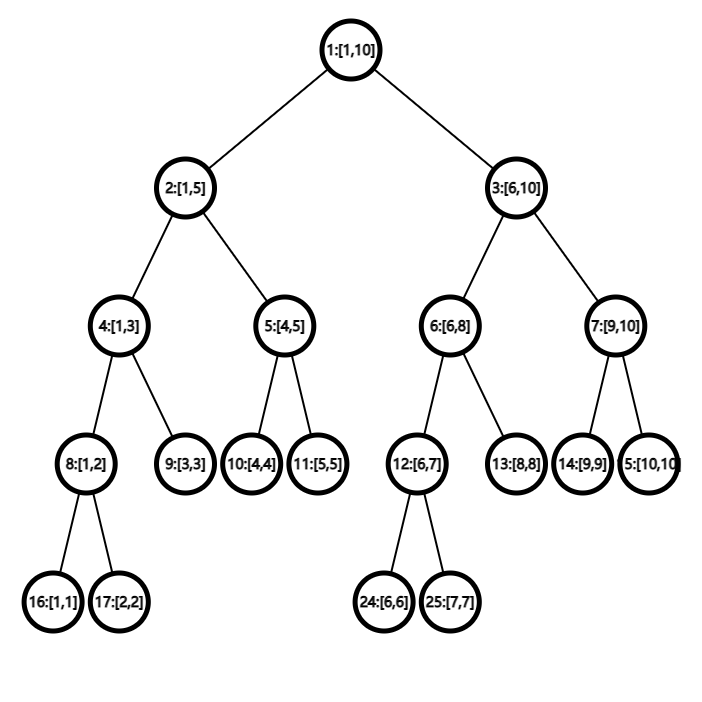
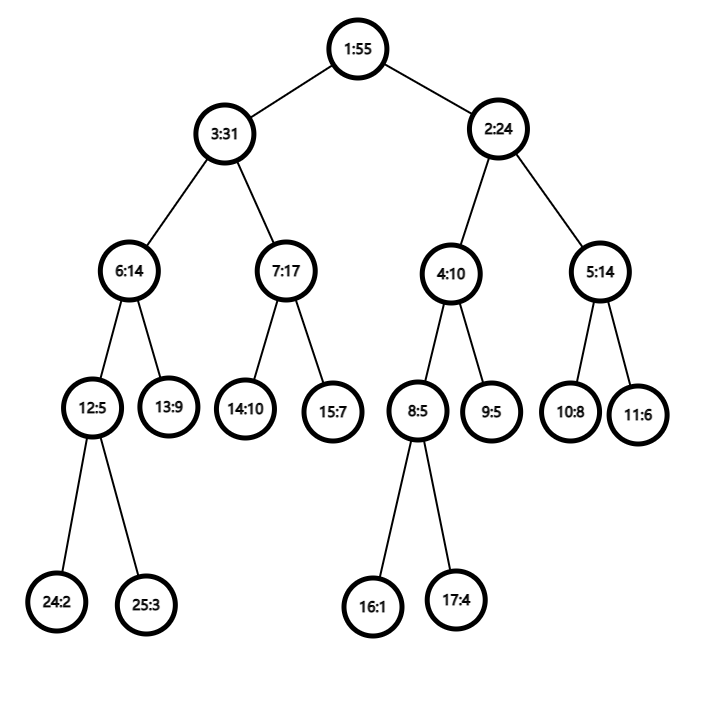
这样在查询区间 \([4,9]\) 的和时,只需要查询结点 \(5,6,14\) 这三个结点的和就行了。一次查询最多有 \(2 \log N\) 个结点,因此时间复杂度为 \(\mathcal{O}(\log N)\)。
下面给出区间查询的代码。若要查询区间 \([x,y]\),现在的结点为 \(p\),区间为 \([l,r]\),那么分为以下情况:
-
\([l,r]\) 被 \([x,y]\) 完全包含,此时 \(x \le l \le r \le y\)。整个区间都要被查询,因此直接返回结点 \(p\) 的值即可。
-
否则只有部分需要查询。让 \(mid=\lfloor \frac{l+r}{2} \rfloor\),那么左儿子的区间为 \([l,mid]\),右儿子的区间为 \([mid+1,r]\)。若 \(x \le mid\),那么左儿子需要查询。若 \(y \ge mid+1\) 即 \(mid+1 \le y\),那么右儿子需要查询。两边查询的和即为这次查询的答案。
/* 静态数组版 */
ll query(int p,int l,int r,int x,int y){
if(x<=l&&r<=y){
/*整个区间都要被查询,直接返回结点p的值*/
return t[p];
}
int mid=(l+r)>>1
ll res=0;
if(x<=mid){
/*有部分在左儿子区间*/
res+=query(ls(p),l,mid,x,y);
}
if(mid+1<=y){
/*有部分在右儿子区间 注意不能写else,因为有可能两个儿子区间都需要查询*/
res+=query(rs(p),mid+1,r,x,y);
}
return res;
}
/* 指针版 */
ll query(usi x,usi y,unique_ptr<node> &u,usi l,usi r){
if(x<=l&&r<=y){
return u->sum;
}
usi mid((l+r)>>1);
ll res(0);
push_d(u,l,r);
if(x<=mid){
res+=query(x,y,u->ls,l,mid);
}
if(mid<y){
res+=query(x,y,u->rs,mid+1,r);
}
return res;
}
3. 区间操作与 Lazy-Tag
本节介绍线段树的核心操作 Lazy-Tag,并给出区间修改 \(+\) 区间查询的模板。
在线段树上,如果直接进行区间修改,时间复杂度为 \(\mathcal{O}(N \log N)\)。而 Lazy-Tag 可以将其降为 \(\mathcal{O}(\log N)\)。
- Lazy-Tag 方法
用 \(lz_p\) 统一记录区间 \(p\) 的修改。也就是说,如果整个区间 \(p\) 都需要修改,那么只修改一下 \(lz_p\) 即可。直到要访问这个区间的子区间时,再将这个标记随递归向下传。这样时间复杂度就变为 \(\mathcal{O}(\log N)\) 了。
- 向下传递函数
push_down()
当要访问一个区间的子区间时,应将这个区间的 Lazy-Tag 传递给下面的两个子区间,并删除这个区间的 Lazy-Tag。这样可以保持最后这个区间的值不变。
如果一个线段树的 Lazy-Tag 为加法标记,那么传递的函数如下。
/* 静态数组版 */
void tag(int p,int l,int r,int k){
t[p]+=(r-l+1)*k;
/*打上标记:总值的变化*/
lz[p]+=k;
/*打上标记:Lazy-Tag的变化*/
}
void push_down(int p,int l,int r){
int mid=(l+r)>>1;
tag(ls(p),l,mid,lz[p]);
tag(rs(p),mid+1,r,lz[p]);
/*将Lazy-Tag传递个下面的两个子区间*/
lz[p]=0;
/*清除标记*/
}
/* 指针版 */
void tag(unique_ptr<node> &u,usi l,usi r,ll k){
u->sum+=(r-l+1)*k;
u->lz+=k;
}
void push_d(unique_ptr<node> &u,usi l,usi r){
if(u->lz){
usi mid((l+r)>>1);
tag(u->ls,l,mid,u->lz);
tag(u->rs,mid+1,r,u->lz);
u->lz=0;
}
}
由于是区间加,当没有标记的时候下传相当于加零,不会影响结果,所以可以不判断是否有标记。
- 区间修改函数
update()
此函数的作用是将区间 \([x,y]\) 的值都加上 \(k\)。当到达结点 \(p\),区间 \([l,r]\) 时,分为以下情况:
-
\(x \le l \le r \le y\),即 \([l,r]\) 完全包含在 \([x,y]\) 中。此时只需要更新 Lazy-Tag 即可。
-
否则只有部分需要修改。让 \(mid=\lfloor \frac{l+r}{2} \rfloor\)。若 \(x \le mid\),则左儿子区间部分需要修改,递归修改左儿子。若 \(y \ge mid+1\) 即 \(mid+1 \le y\),则右儿子区间部分需要修改,递归修改右儿子。
/* 静态数组版 */
void update(int p,int l,int r,int x,int y,int k){
if(x<=l&&r<=y){
/*整个区间都要修改,则只修改Lazy-Tag*/
tag(p,l,r,k);
return;
}
push_down(p,l,r);
/*一定要先下传 Lazy-Tag*/
int mid=(l+r)>>1;
if(x<=mid){
/*左儿子区间部分需要修改*/
update(ls(p),l,mid,x,y,k);
}
if(mid+1<=y){
/*右儿子区间部分需要修改*/
update(rs(p),mid+1,r,x,y,k);
}
push_up(p);
/*更新节点*/
}
/* 指针版 */
void update(usi x,usi y,ll k,unique_ptr<node> &u,usi l,usi r){
if(x<=l&&r<=y){
tag(u,l,r,k);
return;
}
usi mid((l+r)>>1);
push_d(u,l,r);
if(x<=mid){
update(x,y,k,u->ls,l,mid);
}
if(mid<y){
update(x,y,k,u->rs,mid+1,r);
}
push_u(u);
}
- 模板代码
4. 线段树的基础应用
1. 区间乘法
设加法标记为 \(z_1\) 再使用一个乘法标记 \(z_2\)。初始时都为 \(1\)。
- 打加法标记
设对结点 \(p\) 打,区间为 \(l,r\),标记为 \(k\),则 \(z_{1_p} \gets z_{1_p}+k,t_p \gets t_p+(r-l+1) \times k\)。
- 打乘法标记
设对结点 \(p\) 打,区间为 \(l,r\),标记为 \(k\),则 \(z_{1_p} \gets z_{1_p} \times k,z_{2_p} \gets z_{2_p} \times k,t_p \gets t_p \times k\)。
原因:
设该区间的实际总和为 \(a\),则 \(a=t_p \times z_{2_p}+z_{1_p}\)。如果将区间都乘上 \(k\),则 \(a \gets a \times k=(t_p \times z_{2_p}+z_{1_p}) \times k=(t_p \times k) \times (z_{2_p} \times k)+z_{1_p} \times k\)。相对于之前,\(t_p,z_{1_p},z_{2_p}\) 都比原来乘上了 \(k\)。
- 向下传递标记
先将该结点的乘法标记下传并清空,再将加法标记下传并清空。
本题需要取模,实现比较麻烦。可以参考代码理解。
2. 区间开方
本题的操作是区间开方 \(+\) 区间查询,但区间开方不能直接用 Lazy-Tag 实现。本题的关键是:一个数如果被开方 \(7\) 次,那么它一定会变为 \(1\),后面再怎么开方也还是 \(1\)。于是我们可以记录一个区间中是否有不为 \(1\) 的数,在修改时,如果都为 \(1\),直接跳过。
如果到达了一个区间,整个区间都要修改,但其中有不为 \(1\) 的数,怎么办呢?
在上面的区间加法中,如果整个区间都要修改,那么直接更新 Lazy-Tag。在本题中,我们可以继续向下递归修改。这样的话就可以进行区间修改了。
那么时间复杂度如何呢?每个数开方 \(7\) 次的话,只是多了个常数,时间复杂度依旧为 \(\mathcal{O}(M \log N)\)。
3. 区间赋值
只需要用一个新的 Lazy-Tag 记录区间赋值即可。在区间赋值时,要清除原有的区间加法标记。
区间赋值的初始值不能再为 \(0\) 了,要设为一个不等于任何数列中的数的数,比如 \(10^{18}\)。
4. 线段树上二分
本题可以用 \(t_p\) 表示子树 \(p\) 中空花瓶的数量,\(z1_p\) 表示子树 \(p\) 代表的区间是否都被清空了,\(z2_p\) 表示子树 \(p\) 代表的区间是否都插满花了。
对于操作 \(1\),可以在区间 \([a,n-1]\) 中二分出第 \(1\) 个空花瓶的位置 \(l\) 与第 \(f\) 个空花瓶的位置 \(r\),然后将区间 \([l,r]\) 都插满花。
对于操作 \(2\),直接将区间 \([a,b]\) 清空即可。
5. 离散化
本题的空间限制为 \(64MB\)。如果直接用线段树做,原树与 Lazy-Tag 两个数组大约需要 \(76MB\)。此时我们需要离散化。
如果我们用结点来表示墙上的一个点的话,那么在离散化时需要在不连续的两个数之间再插一个数。比如先后贴 \(3\) 张海报 \([1,5],[1,2],[4,5]\),那么直接离散化后是 \([1,4],[1,2],[3,4]\),最后的结果为 \(1,2\) 号点是海报二,\(3,4\) 号点是海报三,共有两种。但实际上 \(3\) 的位置还有海报一。
离散化后就是标准的线段树区间赋值。最后可以用 sort\(+\)unique 去重。
5. 区间最值和区间历史最值
- 区间最值基本题
修改区间最值试着这样的操作:对于序列 \(\{a_1,a_2,\dots,a_N\}\),每次给定 \(l,r,k\),使所有 \(l \le i \le r\) 的 \(a_i\) 改为 \(\min(a_i,k)\)。
下面是一道模板题。
本题不能直接用 Lazy-Tag 进行操作。对于每个结点,可以定义 \(4\) 个标记:区间和 \(su\),区间最大值 \(ma\),严格次大值 \(se\) 和最大值个数 \(num\)。若没有严格次大值,则 \(se=-1\)。
对于操作 \(0\),即用 \(\min(a_i,k)\) 替换 \(l \le i \le r\) 的 \(a_i\),可以分为以下几种情况:
-
\(ma \le k\),此次修改不会影响结点,直接退出。
-
\(se \le x<ma\),此次修改只影响最大值,打上标记并退出。
-
否则就继续递归左右儿子。
在打标记的时候,不用另开一个值,直接修改区间最大值 \(ma\)。在下传的时候,按最大值 \(ma\) 来打标记。
那么时间复杂度如何呢?每次操作 \(0\) 有以下几种情况:
-
\(x\) 比所有元素都大。此时不需要修改,时间复杂度为 \(\mathcal{O}(1)\)。
-
\(x\) 比所有元素都小。此时所有结点都需要修改,时间复杂度为 \(\mathcal{O}(N \log N)\)。但是如果这样操作一次,后面的所有操作(包括操作 \(1,2\))都是 \(\mathcal{O}(1)\)。
-
否则为一般情况,平均时间复杂度为 \(\mathcal{O}(\log N)\)。
\(M\) 次操作后,时间复杂度约为 \(\mathcal{O}(M \log N)\)。
6. 区间合并
线段树适合做区间合并。
本题可以用 1 表示村庄正常,0 表示被摧毁。
在线段数中维护两个值:前缀最大连续 1 的个数 \(pre\) 和后缀最大连续 1 的个数 \(suc\)。在向上更新的时候,可以根据左右儿子的 \(pre,suc\) 值来计算父节点的两个值。设父节点为 \(p\),父节点的区间长度为 \(len\)。下面给出 \(pre\) 值的计算方法,读者可以推导出 \(suc\) 值的计算方法。
- \(ls_{pre}=len-\lfloor \frac{len}{2} \rfloor\)
此时左儿子区间全部为 1,父节点的 \(pre\) 值再加上 \(rs_{pre}\)
- 其他情况
此时左儿子的区间不全为 1,父节点的 \(pre\) 值等于左儿子的 \(pre\) 值。
那么便可以完成操作:
- 摧毁村庄
将该位置的值改为 0,并更新所有相关结点的 \(pre\) 与 \(suc\) 值。
- 重建村庄
用一个栈记录被毁村庄的顺序。将重建村庄的位置改为 1,并更新所有相关节点的 \(pre\) 与 \(suc\) 值。
- 查询
要查询村庄 \(x\) 能到达的村庄个数,在到达结点 \(p\),区间为 \(l,r\) 时:
-
如果 \(x \le mid\)
-
- 如果 \(x+ls_{suc}>mid\)
这说明 \(x\) 右边连续的 1 到达了 \(mid\) 的位置,此时答案应该加上 \(rs_{pre}\)。
-
- 否则
继续向左子树递归查询。
- 否则
处理方式与 \(x \le mid\) 时相似。
这样本题就解决了。
本题需要维护 \(su,pre,suc,z1,z2\),其中 \(su\) 是区间最长连续 1 的个数。因为有区间修改,所以 \(z1\) 标记是否有修改为 0,\(z2\) 标记是否有修改为 0。
在打 \(z1\) 标记时,置 \(su=pre=suc=0\)。在打 \(z2\) 标记时,置 \(su=pre=suc=len\),\(len\) 为区间长度。
在向上更新时,\(p_{su}=\max(ls_{sum},rs_{sum},ls_{suc}+rs_{pre})\)。
在查询时,先判断是否 \(1_{su} \ge k\)。如果是,依次判断下面的情况,并把答案区间区间赋值为 0,否则直接返回 \(0\)。
- \(ls_{su} \ge k\)
查询左儿子区间。
- \(ls_{suc}+rs_{pre} \ge k\)
中间的区间满足条件,返回该区间的左端点:\(mid-ls_{suc}+1\)。
- 否则
查询右儿子区间。
还要注意的是本题有多组数据。
7. 扫描线
扫描线算法是线段树的经典应用,它能解决矩阵面积并、矩阵周长并、多边形面积等几何问题。
1. 矩阵面积并
下图是两个矩形 \(S,W\)。可以将其转化为三个矩形 \(A,B,C\),总面积不变。

矩阵面积 \(=\) 长 \(\times\) 宽。它们的宽很容易计算,但它们的长就比较麻烦了。
对于一个矩形,用入边表示它下面的边,出边表示它上面的边。这样从下到上扫描时,如果遇到入边,就说明进入了一个矩形;如果遇到出边,就说明离开了一个矩形。在上图(c)中,矩形 \(S\) 的入边是边 \(1\),出边是边 \(3\)。
用 \(P_1,P_2,P_3\) 分别表示从左到右的 \(3\) 条线段的长度。所以 \(A\) 的宽 \(=P_1+P_2\),\(B\) 的宽 \(=P_1+P_2+P_3\),\(C\) 的宽 \(=P_2+P_3\)。求它们的宽,实际上就是判断这些线段要不要计算进去。如计算 \(C\) 是 \(P_2,P_3\) 需要计算进去。
定义标志 \(T_1,T_2,T_3\) 分别判断 \(P_1,P_2,P_3\) 是否要计算进去。在遇到入边时,\(T\) 加 \(1\);在遇到出边时,\(T\) 减 \(1\)。可以发现,当 \(T>0\) 是需要计算进去。得到 \(T\) 值,就可以计算矩形 \(A,B,C\) 的宽了。
整个算法就使用扫描线从下到上扫过所有矩形,每次扫描都计算其中一层的面积。这就是扫描线算法。
以上模型,如何用线段树实现?可以让线段树的一个结点表示区间范围,如上图用结点 \(1,2,3\) 分别表示 \(P_1,P_2,P_3\)。将这些点看为叶子节点,从下向上扫描,如果是入边就加入线段,如果是出边就删除线段。
用线段树实现扫描线需要离散化。用结点 \(1,2,3\) 分别表示 \(P_1,P_2,P_3\) 即可。
时间复杂度为 \(\mathcal{O}(M \log N)\)。
-
读入所有矩形,记录入边和出边。
-
对所有边按 \(y\) 坐标排序,确定扫描顺序。
-
对 \(x\) 坐标做离散化。
-
从下向上扫描线段,用扫描到的线段更新线段树,每个结点的值是扫描线确定的新矩形。
-
对所有矩形求和。
2. 矩阵周长并

周长问题和面积问题的思路差不多,但是复杂一点。下面给出两种方法。
1. 做两次扫描
总周长 \(=\) 总横线长 \(+\) 总竖线长。
以横线为例。将所有横线按 \(y\) 坐标升序排序,并分为入边和出边,分别用 \(1,-1\) 表示。
从下到上扫描,每次扫描就记录这部分的横线值。应计入的长度就等于现在总区间被覆盖的长度与上一次总区间被覆盖的长度之差的绝对值。这个不难理解。在新计入线段后,会有两种情况:
- 这条线段在总区间的内部
比如上图中最上方大矩形中的小矩形。在更新长度后,总长度不会变。而实际周长确实没有包含这条边。
- 这条线段一部分在总区间以外
比如上图中最左侧矩形的下面那条边。扫过这条线段后,区间总长度会加上它的左边部分,也就是说,现在的总长度与上次的总长度差了左边部分的长度。而实际周长确实计算了这部分的长度。
因此这个方法是正确的。同理可以计算竖线。
2. 做一次扫描
其实做一次就够了。在计算横线的同时可以将竖线也计算出来。
用 \(num\) 表示应计入总长度的竖边的数量,\(sum\) 表示计算的总周长。
每次扫到入边时,如果没有与它 \(y\) 坐标相同且已经扫过的入边,那么就会新加入两条线段,\(num \leftarrow num+2\)。这两条线段的长度即为这条横边与下一条横边的距离。设这个距离为 \(d\),则 \(sum \leftarrow sum+d \times num\)
每次扫到出边时,如果没有与它 \(y\) 坐标相同且已经扫过的出边,那么就会减少两条线段,\(num \leftarrow num-2\)。
这样就能计算出总周长了。



