二叉搜索树

1. 特征

BST 是一种树。它的特征为一个结点左子树结点的权值 \(\le\) 这个结点的权值 \(\le\) 右子树结点的权值。这样可以使它的中序遍历是一个递增的序列。

下图就是一个 BST：

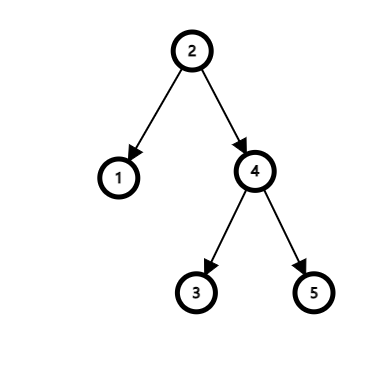
2. 建树

比如说插入结点顺序为 \(a,b,c\)。

先插入 \(a\)。\(a\) 为根节点。

然后插入 \(b\)。如果 \(b<a\)，就在 \(a\) 的左子树插。否则在右子树插。

然后插入 \(c\)。如果 \(c<a\)，就在 \(a\) 的左子树插。如果 \(b\) 已经在这里了，就继续和 \(b\) 比较 \(\ldots\)。

就这样不断比较，直到到达一个空节点。可以用递归实现。

3. 形态

如果给定结点的顺序一定，那么它的形态唯一。

最后形成的 BST 形态可能很好，也可能很坏。

如果插入的顺序为一个递增序列，那么只会在右子树上插，它会变成一条链，查找一次复杂度为 \(\mathcal{O}(N)\)。

如果插入的顺序没有规律，那么这个树就比较平衡。查找一次复杂度约为 \(\mathcal{O}(\log N)\)。

所以使用 BST 的基本问题就是如何维护平衡。常用的方法有替罪羊树、Treap 树、FHQ Treap 树和 Splay 树。