Treap 树
1. 概念
Treap 树是维护二叉查找树平衡的一种方法。它的核心思想是给每个结点设置一个随机的优先级,使它成为一个堆,即父亲的优先级一定小于(或大于)孩子的优先级。大于则为大根堆,小于则为小根堆。本节使用的是大根堆。这样就可以实现概率上的平衡。
下图是一棵 Treap 树的建树方法。
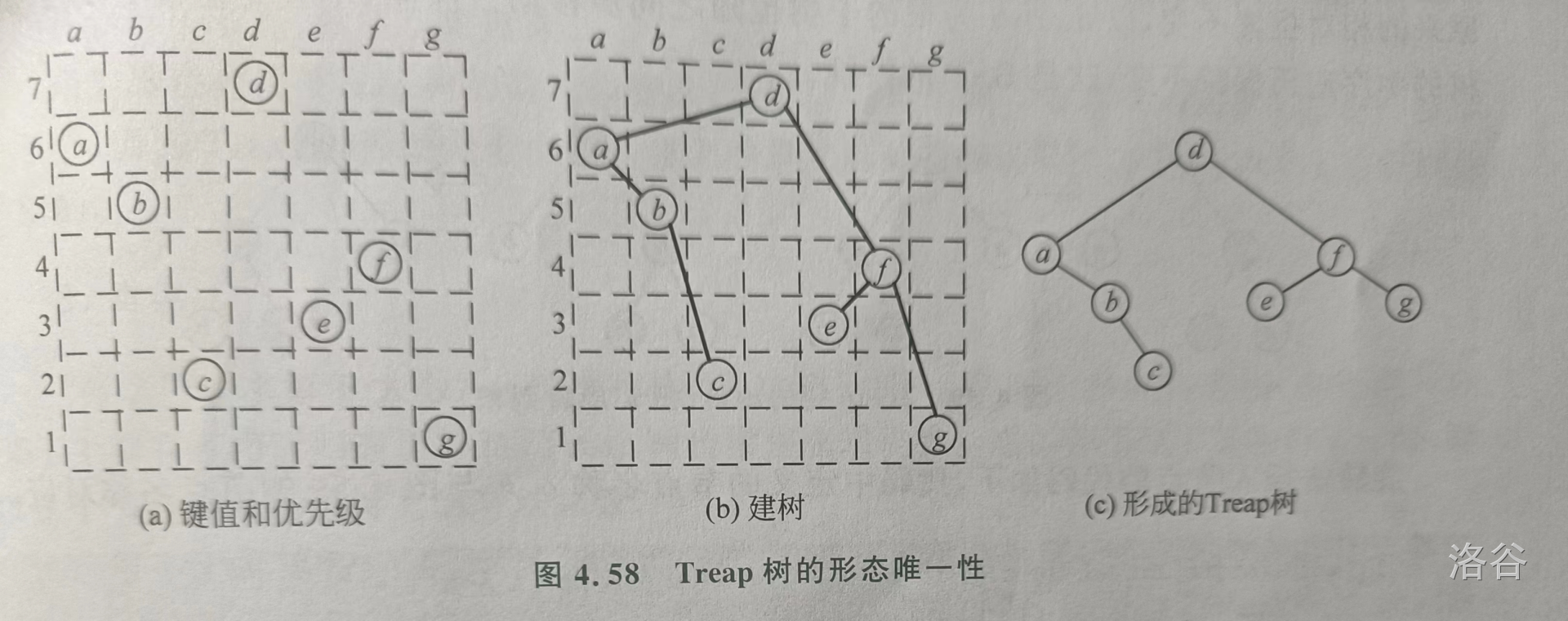
其中字母是键值,数字是优先级。可以发现,建好树后,中序遍历键值递增,且按优先级满足大根堆。
在 Treap 中,通常要维护以下的值:
子树大小 \(sz\),权值 \(vl\),优先级 \(pri\),左儿子 \(ls\),右儿子 \(rs\)。
我们通常还会用一个栈保存可以使用的结点,插入结点时从栈顶取一个结点,删除时将结点入栈。这样可以节省很多空间。
2. 旋转法
旋转法是 Treap 树调节平衡的经典方法。它的示意图如下:
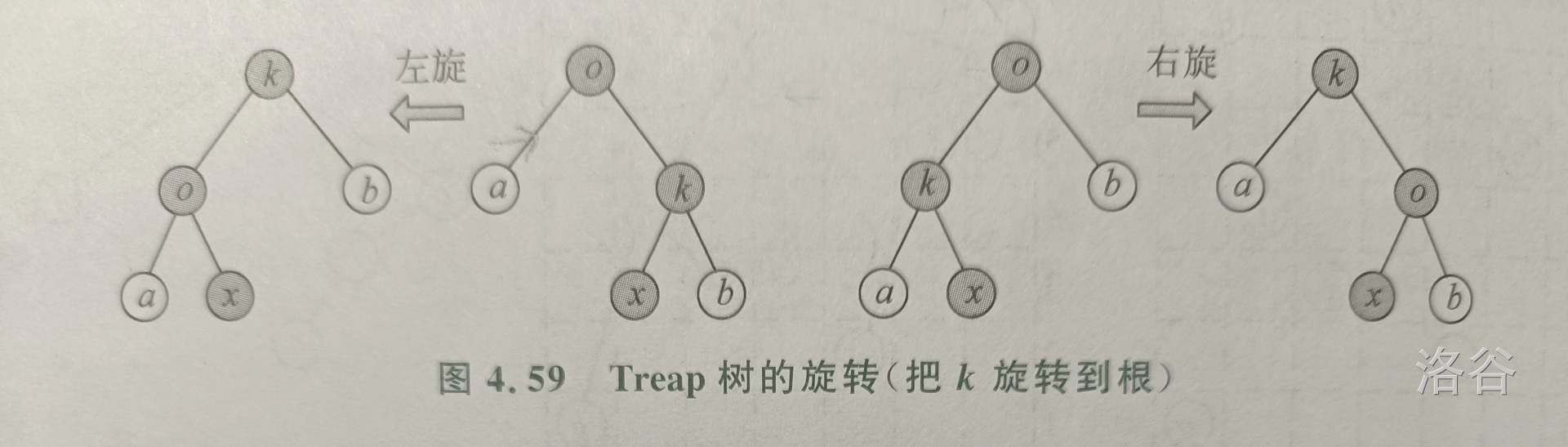
代码如下:
void rtt(int &f,bool l){
/*旋转节点为f,l为是否左旋*/
int u;
/*u为新的根节点*/
if(l){
u=t[f].rs;
t[f].rs=t[u].ls;
t[u].ls=f;
}else{
u=t[f].ls;
t[f].ls=t[u].rs;
t[u].rs=f;
}
push_up(u);
/*更新u子树大小*/
push_up(f);
/*更新f子树大小*/
f=u;
/*更新根节点*/
}
通过旋转法,可以实现以下操作:
insert:插入结点 \(k\)
根据权值,找到一个合适的位置插入结点 \(k\),并为它分配优先级。接下来只要它的优先级比它的父亲大,就将它向上调整。在堆中,我们可以直接交换,但这里直接交换可能会破坏单调性,需要用旋转法来调整。
代码如下:
void insert(int k,int &u=root){
/*插入结点k,现在的子树是u*/
if(!u){
/*这里没有结点,可以直接插入*/
u=sta[--top];
/*新建节点*/
init_node(u,k);
return;
}
if(k<t[u].vl){
insert(k,t[u].ls);
/*插入左子树*/
if(t[t[u].ls].pri>t[u].pri){
/*左儿子的优先级更大,就右旋*/
rtt(u,false);
}
}else{
insert(k,t[u].rs);
/*插入右子树*/
if(t[t[u].rs].pri>t[u].pri){
/*右儿子的优先级更大,就左旋*/
rtt(u,true);
}
}
push_up(u);
}
erase:删除结点 \(k\)
如果 \(k\) 是叶子节点,直接删除。
如果 \(k\) 只有一个子树,就将子树提上来。
否则说明它有两个子节点。将这两个子节点中优先级更大的那个旋转上来,这样 \(k\) 就向下移动一层,直到满足前两种情况之一。
代码如下:
void erase(int k,int &u=root){
/*删除结点k,此时子树为u*/
if(k==t[u].vl){
if(!t[u].ls&&!t[u].rs){
sta[top]=u;++top;
u=0;return;
/*叶子节点直接删除*/
}else if(!t[u].ls||!t[u].rs){
sta[top]=u;++top;
u=t[u].ls+t[u].rs;return;
/*有一个子树为空,直接删除*/
}else if(t[t[u].ls].pri>t[t[u].rs].pri){
rtt(u,false);
erase(k,t[u].rs);
/*左儿子优先级大,右旋*/
}else{
rtt(u,true);
erase(k,t[u].ls);
/*右儿子优先级大,左旋*/
}
}else if(k<t[u].vl){
erase(k,t[u].ls);
/*在左子树上*/
}else{
erase(k,t[u].rs);
/*在右子树上*/
}
push_up(u);
}
rank:求 \(k\) 的排名(比 \(k\) 小的数的个数)
排名为比 \(k\) 小的数的个数加一。下文中的 \(u\) 都代表当前节点。从根节点开始递归,如果 \(u_{vl}>=k\),就递归左子树。否则答案为递归右子树的答案 \(+u_{ls_{sz}}+1\),因为左子树的结点都比 \(u\) 小。
代码如下:
int rank(int k,int u=root){
/*查询比k小的数的个数,此时子树为u*/
if(!u){
return 0;
}else if(k<=t[u].vl){
/*比k小的数都在左子树*/
return rank(k,t[u].ls);
}else{
/*在右子树上*/
return rank(k,t[u].rs)+t[t[u].ls].sz+1;
/*右子树上的排名+左子树大小+1*/
}
}
kth:求排名为 \(k\) 的数
从根结点开始递归,如果 \(k=ls_{sz}+1\),那么答案就为 \(u_{vl}\)。否则如果 \(k<u_{ls_{sz}}+1\),就在左子树上找,否则在右子树上找第 \(k-u_{ls_{sz}}-1\) 小的值。
代码如下:
void kth(int u,int k,int &ret){
/*查询排名为k的数,此时子树为u,最后答案为ret*/
if(k==t[t[u].ls].sz+1){
/*找到了*/
ret=t[u].vl;
}else if(k<t[t[u].ls].sz+1){
/*在左子树上*/
kth(t[u].ls,k,ret);
}else{
/*在右子树上*/
kth(t[u].rs,k-t[t[u].ls].sz-1,ret);
}
}
pre:求 \(k\) 的前驱
答案即为 kth(rank(k))。
suc:求 \(k\) 的后继
答案即为 kth(rank(k+1)+1)。
代码中,大部分操作都使用递归,改成循环可以进一步优化。

