最短路径
最短路算法主要有 Floyd,Dijkstra,Bellman-Ford,SPFA,Johnson 这五种算法。
Floyd 用来处理全源最短路,可以处理负边权。时间复杂度为 \(\mathcal{O}(N^3)\)。
Dijkstra 用来处理单源最短路,不能处理负边权。时间复杂度最优为 \(\mathcal{O}{(M \log M)}\)。
Bellman-Ford 用来处理单源最短路,可以处理负边权。时间复杂度为 \(\mathcal{O}{(NM)}\)。
SPFA 用来处理单源最短路,可以处理负边权。时间复杂度最差为 \(\mathcal{O}{(NM)}\),但一般会更优。
Johnson 用来处理全源最短路,可以处理负边权。时间复杂度为 \(\mathcal{O}{(NM \log M)}\)。
下面就来讲解一下这六种算法。
1. Floyd
Floyd 的思想是:从 \(i\) 到 \(j\) 时,可以考虑先从 \(i\) 到 \(k\) 再从 \(k\) 到 \(j\)。
用 \(ds_{i,j}\) 表示点 \(i\) 到点 \(j\) 的距离,初始时如果 \(i\) 到 \(j\) 有边,\(ds_{i,j}\) 就是边长,否则就是无限大。
枚举 \(k,i,j\),将 \(ds_{i,j}\) 与 \(ds_{i,k}+ds_{k,j}\) 去最小值。这样 \(N\) 轮过后,\(ds_{i,j}\) 即为 \(i \sim j\) 的最短路。
注意一定要先枚举 \(k\)。
2. Dijkstra
朴素版
Dijkstra 的核心思想是贪心。初始时标记所有点的距离为无限大,到初始点的距离为 \(0\)。
用 \(g_{i,j}\) 表示结点 \(i\) 到结点 \(j\) 的距离,\(ds_i\) 表示初始点到结点 \(i\) 的距离,\(vs_i\) 表示结点 \(i\) 是否被标记过。
接下来执行 \(N-1\) 次,先找到距离最短的且没有标记的点 \(k\),然后标记 \(vs_k \leftarrow true\)。接下来遍历没标记的所有点,让第 \(j\) 个点的距离变为点 \(j\) 的距离与点 \(k\) 的距离加上点 \(k\) 到点 \(j\) 的距离的最小值,也就是 \(ds_j \leftarrow \min(ds_j,ds_k+g_{k,j})\)。这样就可以取得最小值了。
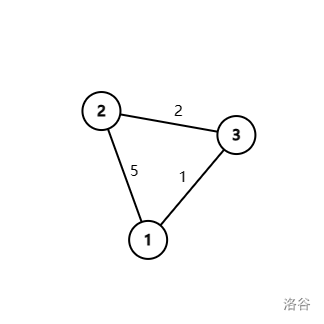
比如上面这张图,三个数组的值都如下:
| \(g\) | 1 | 2 | 3 |
|---|---|---|---|
| 1 | \(\infty\) | 5 | 1 |
| 2 | 5 | \(\infty\) | 2 |
| 3 | 1 | 2 | \(\infty\) |
| index | 1 | 2 | 3 |
|---|---|---|---|
| \(ds\) | 0 | \(\infty\) | \(\infty\) |
| \(vs\) | \(false\) | \(false\) | \(false\) |
接下来找到最近的点。显然这个点为 \(1\)。接下来标记 \(vs_1 \leftarrow true\),然后遍历一遍所有没标记的点,让 \(ds_j \leftarrow \min(ds_j,ds_1+g_{1,j})\)。此时的数组如下。
| index | 1 | 2 | 3 |
|---|---|---|---|
| \(ds\) | \(\min(0,0+\infty)=0\) | \(\min(\infty,0+5)=5\) | \(\min(\infty,0+1)=1\) |
| \(vs\) | \(true\) | \(false\) | \(false\) |
接下来没有标记过的且距离最短的点为 \(3\)。于是继续更新其它的点:
| index | 1 | 2 | 3 |
|---|---|---|---|
| \(ds\) | \(\min(0,1+1)=0\) | \(\min(5,1+2)=3\) | \(\min(1,1+\infty)=1\) |
| \(vs\) | \(true\) | \(false\) | \(true\) |
最后 \(ds_i\) 就是初始点到点 \(i\) 的最短距离了。
时间复杂度为 \(\mathcal{O}(N^2)\)。
如果是负边权,如图。
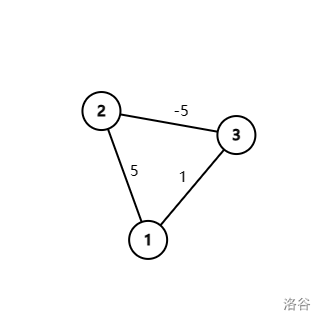
在第二轮循环时 Dijkstra 会把 \(vs_3\) 标记为 \(true\),且 \(ds_3\) 为 \(1\)。但真正的最短路是先到点 \(2\) 再到点 \(3\),长度为 \(0\)。所以 Dijkstra 只支持正边权的最短路。
优先队列优化
朴素版的 Dijkstra 的时间复杂度为 \(\mathcal{O}(N^2)\),在 \(N \le 10^5\) 时不能通过。这时我们需要优化。
可以发现,在更新其它点的距离时,只需要取最小值即可。容易想到使用优先队列。
优先队列的作用是 \(\mathcal{O}(\log N)\) 插入元素,\(\mathcal{O}(1)\) 访问最大值或最小值,\(\mathcal{O}(\log N)\) 删除最大值或最小值元素。这里不再讲原理。
我们使用链式前向星存图。使用以长度为排序方式的小根堆。将初始点加入优先队列,只要队列里有元素,就取出优先队列的队首元素 \(u\)。如果 \(u\) 还没有标记,就标记 \(vs_u \leftarrow true\),接着遍历 \(u\) 所连接的点 \(v\),用 \(w\) 保存边权,更新 \(ds_v \leftarrow \min(ds_v,ds_u+w)\)。如果 \(vs_v\) 为 \(false\),就将点 \(v\) 加入优先队列。
查找的时间复杂度为 \(\mathcal{O}(\log M)\),更新的时间复杂度为 \(\mathcal{O}(M)\),所以使用优先队列优化后时间复杂度变为 \(\mathcal{O}(M \log M)\),可以通过。
本题只需将上一题代码的数据范围改一下即可通过。
3. Bellman-Ford
遇到负权值时,需要使用 Bellman-Ford 或 SPFA。先来讲一下 Bellman-Ford。
思想为枚举每条边,如果走这条边比不走这条边距离更短,就更新距离。
用 \(u_i,v_i,w_i\) 表示第 \(i\) 条边从 \(u_i\) 指向 \(v_i\),权值为 \(w_i\)。
更新 \(N\) 次,每次枚举每条边,如果 \(ds_{u_i}+w_i<ds_{v_i}\),就更新 \(ds_{v_i} \leftarrow ds_{u_i}+w_i\)。
更新 \(N\) 次是因为一个图中最短路径可能要经过 \(N-1\) 条边。这样时间复杂度为 \(\mathcal{O}(NM)\)。
接下来将用 Bellman-Ford 实现 HDU-2544。
4. SPFA
Bellman-Ford 的时间复杂度很高,所以我们需要优化。
可以发现如果一个点的距离没有更新,那么下一轮从这个点到达的其它的点的距离也不会更新。所以我们可以用队列来优化。
将初始点加入队列。每次取出队首元素,遍历它的所有出边,如果距离可以更新,就更新距离,并把更新的点加入队列。
为了防止重复入队,可以用 \(vs_i\) 表示点 \(i\) 是否在队列中。更新时如果 \(vs_v=false\) 才能入队。出队时要让 \(vs_u \leftarrow false\),入队时要让 \(vs_v \leftarrow true\)。
SPFA 的时间复杂度最差为 \(\mathcal{O}(NM)\),一般情况下会更优,但有时会遇到良心出题人。所以在没有负权值的图中,一定要用 Dijkstra。
5. Johnson
证明参考这里。
建立一个节点 \(0\),到每个点的距离都为 \(0\)。然后用 SPFA 给这个点跑最短路,同时判断负环,用 \(d_i\) 表示 \(0\) 到 \(i\) 的最短路。接下来遍历每一条边,将这条边的权值加上 \(d_u-d_v\)。接下来跑 \(N\) 次 Dijkstra,在第 \(u\) 次以 \(u\) 为起点,\(ds_i\) 表示 \(u\) 到 \(i\) 的距离。完成后 \(ds_i-d_i+d_u\) 即为距离。



